Xác định vectơ, các khái niệm vectơ, vectơ cùng phương
Bài tập Toán 10: Xác định vectơ, vectơ cùng hướng
Trong chương trình Toán 10, phần vectơ đóng vai trò nền tảng cho nhiều kiến thức hình học và đại số ở các lớp học sau. Việc hiểu rõ cách xác định vectơ, nắm vững các khái niệm vectơ và nhận biết vectơ cùng phương sẽ giúp học sinh dễ dàng vận dụng vào bài toán hình học, chứng minh song song, vuông góc và tọa độ vectơ. Bài viết này tổng hợp kiến thức trọng tâm, ví dụ minh họa có đáp án chi tiết, giúp bạn hiểu bản chất, phân biệt các loại vectơ và vận dụng linh hoạt trong giải toán.
A. Kiến thức cần nhớ về Vectơ
- Vectơ là đoạn thẳng có hướng, nghĩa là trong hai điểm mút của đoạn thẳng đã chỉ rõ điểm nào là điểm đầu, điểm nào là điểm cuối.
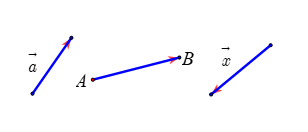
- Vectơ có điểm đầu là A, điểm cuối là B ta kí hiệu :
\(\overrightarrow{AB}\) - Vectơ còn được kí hiệu là: \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{x},\overrightarrow{y},...\)
- Vectơ – không là vectơ có điểm đầu trùng điểm cuối. Kí hiệu là \(\overrightarrow{0}\).
- Đường thẳng đi qua điểm đầu và điểm cuối của vectơ gọi là giá của vectơ
- Hai vectơ có giá song song hoặc trùng nhau gọi là hai vectơ cùng phương
- Hai vectơ cùng phương thì hoặc cùng hướng hoặc ngược hướng.
B. Ví dụ minh họa
Ví dụ 1: a) Cho hai điểm phân biệt \(A,B\). Có bao nhiêu vectơ (khác\(\overrightarrow{0}\)) có điểm đầu và điểm cuối lấy từ các điểm \(A,B\)
b) Cho tam giác \(ABC\) có thể xác định được bao nhiêu vectơ (khác vectơ không) có điểm đầu và điểm cuối là đỉnh \(A\),\(B\),\(C\)?
c) Cho bốn điểm \(ABCD\)có thể xác định được bao nhiêu vectơ (khác vectơ không) có điểm đầu và điểm cuối là đỉnh \(A\),\(B\), \(C\),\(D\)?
Hướng dẫn giải
a) Có thể xác định được \(2\) vectơ (khác \(\overrightarrow{0}\)) là \(\overrightarrow{AB}\) và \(\overrightarrow{BA}\) .
b) Hình vẽ minh họa:
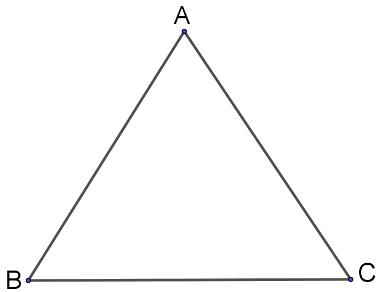
Ta có các vectơ đó là: \(\overrightarrow{AB},\overrightarrow{AC},\overrightarrow{BA},\overrightarrow{BC},\overrightarrow{CA},\overrightarrow{CB}\).
c) Có thể xác định được \(12\) vectơ (khác \(\overrightarrow{0}\)) là \(\overrightarrow{AB}\),\(\overrightarrow{BA}\),\(\overrightarrow{AC},\ \overrightarrow{CA}\) , \(\overrightarrow{AD},\
\overrightarrow{DA}\), \(\overrightarrow{BC},\
\overrightarrow{CB}\), \(\overrightarrow{BD},\
\overrightarrow{DB}\),\(\overrightarrow{CD},\
\overrightarrow{DC}\)
Ví dụ 2: Cho hình bình hành \(ABCD\) , tâm O. Gọi M, N lần lượt là trung điểm của AD, BC.
a) Kể tên hai vectơ cùng phương với \(\overrightarrow{AB}\), hai vectơ cùng hướng với \(\overrightarrow{AB}\), hai vectơ ngược hướng với \(\overrightarrow{AB}\).
b) Chỉ ra một vectơ bằng vectơ \(\overrightarrow{MO}\)và một vectơ bằng vectơ \(\overrightarrow{OB}\).
c) Chỉ ra các vectơ đối của vectơ \(\overrightarrow{AD}\).
Hướng dẫn giải
Hình vẽ minh họa:
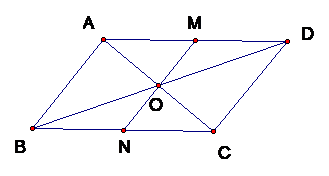
a) Hai vectơ cùng phương với \(\overrightarrow{AB}\): \(\overrightarrow{CD}\), \(\overrightarrow{DC}\).
Hai vectơ cùng hướng với \(\overrightarrow{AB}\): \(\overrightarrow{DC}\); \(\overrightarrow{MO}\)
Hai vectơ ngược hướng với \(\overrightarrow{AB}\): \(\overrightarrow{CD};\overrightarrow{OM}\)
b) Vectơ bằng \(\overrightarrow{MO}\) là \(\overrightarrow{ON}\).
Vectơ bằng \(\overrightarrow{OB}\) là \(\overrightarrow{DO}\).
c) Vectơ đối của vectơ \(\overrightarrow{AD}\) là \(\overrightarrow{DA},\overrightarrow{CB}\).
Ví dụ 3: Cho lục giác đều ABCDEF có tâm O.
a) Tìm các vectơ khác \(\overrightarrow{0}\) và cùng phương với \(\overrightarrow{OA}\) (khác \(\overrightarrow{OA}\))
b) Tìm các vectơ bằng \(\overrightarrow{AB}\) .
c) Tìm các vectơ đối của vectơ \(\overrightarrow{OD}\).
Hướng dẫn giải
Hình vẽ minh họa:
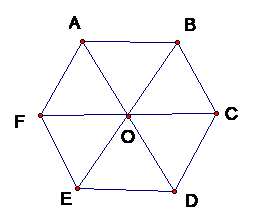
a) Các vectơ khác \(\overrightarrow{0}\) và cùng phương với \(\overrightarrow{OA}\) là:
\(\begin{matrix}\overrightarrow{DA};\overrightarrow{AD};\overrightarrow{BC};\overrightarrow{CB};\overrightarrow{AO}\hfill\\\overrightarrow{OD};\overrightarrow{DO};\overrightarrow{FE};\overrightarrow{EF}\hfill\end{matrix}\)
b) Các vectơ bằng \(\overrightarrow{AB}\) là \(\overrightarrow{OC};\overrightarrow{ED};\overrightarrow{FO}\).
c) Các vectơ đối của vectơ \(\overrightarrow{OD}\) là: \(\overrightarrow{OA},\overrightarrow{DO},\overrightarrow{EF},\overrightarrow{CB}\).
Ví dụ 4: Cho hình thang cân \(ABCD\) có hai đáy là AB và CD. Tìm vectơ:
a) Cùng hướng với \(\overrightarrow{AB}\).
b) Ngược hướng với \(\overrightarrow{AB}\).
c) Chỉ ra các vectơ có độ dài bằng nhau
Hướng dẫn giải
Hình vẽ minh họa:
a) Ta có ABCD là hình thang có hai đáy là AB và CD nên AB // CD.
Khi đó vectơ cùng hướng với vectơ \(\overrightarrow{AB}\) là vectơ \(\overrightarrow{DC}\) (do cùng phương, cùng chiều).
b) Vectơ ngược hướng với vectơ \(\overrightarrow{AB}\) là vectơ \(\overrightarrow{BA}\) và \(\overrightarrow{CD}\)
c) Các vectơ có cùng độ dài là \(\left|
\overrightarrow{AD} \right| = \left| \overrightarrow{DA} \right| =
\left| \overrightarrow{BC} \right| = \ \left| \overrightarrow{CB}
\right|\) và \(\left|
\overrightarrow{AC} \right| = \left| \overrightarrow{CA} \right| =
\left| \overrightarrow{BD} \right| = \ \left| \overrightarrow{DB}
\right|\).
C. Bài tập tự rèn luyện có đáp án chi tiết
Bài tập 1: Quan sát ròng rọc hoạt động khi dùng lực để kéo một đầu của ròng rọc. Chuyển động của các đoạn dây được mô tả bằng các vectơ \(\overrightarrow{a},\ \
\overrightarrow{b},\ \overrightarrow{c}\) (như hình vẽ):
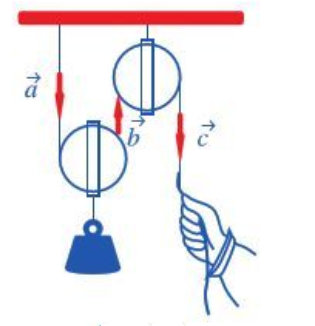
a) Hãy chỉ ra các cặp vectơ cùng phương.
b) Trong các cặp vectơ đó, cho biết chúng cùng hướng hay ngược hướng.
Bài tập 2: Cho tam giác đều \(ABC\) với cạnh có độ dài bằng a.
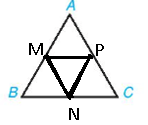
a) Hãy chỉ ra các vectơ có độ dài bằng a và có điểm đầu, điểm cuối là các đỉnh của tam giác \(ABC\). Có cặp vec tơ nào bằng nhau không?
b) Gọi \(M,\ N,\ P\) lần lượt là trung điểm của \(AB,\ BC,\ CA\). Hãy chỉ ra các cặp vectơ bằng nhau
Bài tập 3: Cho \(A,\ B,\ C\) là ba điểm thẳng hàng, \(B\) nằm giữa \(A\) và \(C\). Viết các cặp vectơ cùng hướng, ngược hướng trong những vectơ sau \(\overrightarrow{AB},\overrightarrow{AC},\overrightarrow{BA},\overrightarrow{BC},\overrightarrow{CA},\overrightarrow{CB}\).
Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!
-----------------------------------
Qua bài viết xác định vectơ, các khái niệm vectơ và vectơ cùng phương, bạn đã được hệ thống đầy đủ kiến thức cơ bản nhất của chuyên đề vectơ Toán 10. Hãy ghi nhớ kỹ cách xác định vectơ, các tính chất và điều kiện cùng phương để vận dụng vào các bài toán chứng minh hình học và phần tọa độ vectơ trong mặt phẳng.
