Xét dấu biểu thức lượng giác có đáp án và cách giải chi tiết
Cách xét dấu biểu thức lượng giác có đáp án
Trong chương trình Toán 10, chuyên đề biểu thức lượng giác đóng vai trò quan trọng giúp học sinh hiểu sâu hơn về tính chất, dấu của các giá trị lượng giác. Bài viết xét dấu biểu thức lượng giác có đáp án và cách giải chi tiết sẽ hướng dẫn từng bước cách nhận biết dấu của sin, cos, tan, cot thông qua các bài tập minh họa kèm lời giải chi tiết, giúp học sinh nắm chắc phương pháp và tránh sai sót khi làm bài thi.
A. Cách xét dấu biểu thức lượng giác
Phương pháp giải: Sử dụng bảng xét dấu giá trị lượng giác
Với 
\(0^{0} \leq \alpha \leq
180^{0}\) ta có \(0 \leq \sin\alpha
\leq 1;\ \ - 1 \leq \cos\alpha \leq 1\)
Bảng xét dấu của giá trị lượng giác
|
Góc |
|
|
| \(\sin\alpha\) |
+ |
+ |
| \(\cos\alpha\) |
+ |
- |
| \(\tan\alpha\) |
+ |
- |
| \(\cot\alpha\) |
+ |
- |
B. Ví dụ minh họa xét dấu biểu thức lượng giác
Ví dụ 1: Xét dấu biểu thức: \(P = \cos
x.sinx\) biết \(0^{0} < x <
90^{0}\)
Hướng dẫn giải
Ta có:
\(\cos x > 0;\ \ \sin x >
0\) với \(0{^\circ} < x <
90{^\circ}.\)
Do đó \(P = \cos x.sinx
> 0.\)
Ví dụ 2: Xét dấu biểu thức:\(P =
sin^{2}x.tanx\) biết \(90^{0} < x
< 180^{0}\).
Hướng dẫn giải
Ta có: \(sin^{2,}x > 0;tanx <
0,\) với \(90^{0} < x <
180^{0}\)
Do đó \(P = sin^{2}x.tanx <
0\)
Ví dụ 3: Xét dấu biểu thức: \(P = (cosx -1).\sin x.\tan x\) biết \(0^{0} < x <
90^{0}\).
Hướng dẫn giải
Ta có:
\(P = (cosx - 1)\sin x\frac{\sin x}{\cos x} =(\cos x - 1)\sin^{2}x\frac{1}{\cos x}\)
Lại có:
\(sin^{2}x \geq 1\); \(\cos x - 1 < 0\) ( vì \(0^{0} < x < 90^{0}\))
\(\Leftrightarrow 0 < \cos x < 1\), \(\cos x > 0\)
Ta có bảng tổng kết:
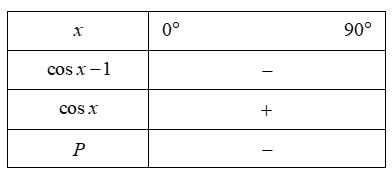
Vậy \(0{^\circ} < x <
90{^\circ}\) thì \(P = (cosx -
1)sinx.tanx < 0\)
Ví dụ 4: Xét dấu của \(P =\sin^{2}x.\cos^{3}x.\tan x\) biết \(45^{0}
< x < 180^{0}\); \(x \neq
90^{0}\).
Hướng dẫn giải
Ta có:
\(sin^{2}x \geq 0\) vói \(45^{0} < x < 180^{0}\)
\(\cos x \geq 0\)với \(45^{0} < x \leq 90^{0}\)
\(\cos x < 0\) với \(90^{0} < x < 180^{0}\)
\(\tan x > 0\)với \(45^{0} < x < 90^{0}\)
\(\tan x < 0\) với \(90^{0} < x < 180^{0}\)
Ta có bảng dấu như sau:
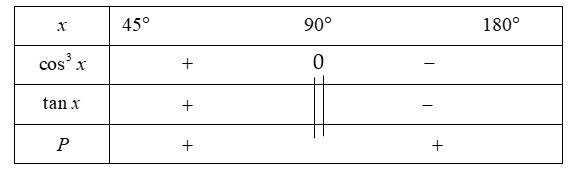
Vậy \(P = \sin^{2}x.\cos^{3}x.\tan x\) luôn luôn dương khi \(45{^\circ} < x <
180{^\circ},\ \ x \neq 90{^\circ}\).
C. Bài tập tự rèn luyện xét dấu biểu thức lượng giác có đáp án chi tiết
Bài tập 1: Xét dấu của \(P = sin^{3}x\cos
x(1 - sin^{9}x),\) biết \(75^{0} < x
< 125^{0}\).
Bài tâp 2: Định \(x\) để \(P = \sin x\cos x > 0,\) biết \(0^\circ < x < 180^\circ\)
Bài tập 3: Định \(x\) để \(T = sin(115{^\circ} - x) > 0,\) biết \(0{^\circ} < x <
180{^\circ}.\)
Bài tập 4: Định \(x\) để \(P = sin^{2}x.(1 - \cos x).cotx > 0\), biết \(30{^\circ} < x < 160{^\circ},\ \
x \neq 90{^\circ}.\)
Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!
-------------------------------------------------
Qua bài viết Xét dấu biểu thức lượng giác có đáp án và cách giải chi tiết, hy vọng các em đã hiểu rõ hơn cách xác định dấu của các hàm lượng giác trong từng góc phần tư. Hãy luyện tập thường xuyên để thành thạo kỹ năng xét dấu và củng cố kiến thức biểu thức lượng giác Toán 10, chuẩn bị tốt cho các kỳ kiểm tra và thi học kỳ.
