Bài tập tích vô hướng của hai vectơ toán 10 Có đáp án chi tiết dễ hiểu
Các dạng bài tích vô hướng lớp 10 có đáp án
Trong chuyên đề Tích vô hướng của hai vectơ Toán 10, việc nắm vững công thức và cách vận dụng vào bài tập là yếu tố quan trọng giúp học sinh hiểu sâu hơn về mối quan hệ giữa vectơ và góc. Bài viết Bài tập tích vô hướng của hai vectơ Toán 10 có đáp án chi tiết dễ hiểu tổng hợp các dạng bài tiêu biểu, hướng dẫn giải từng bước và kèm đáp án chi tiết giúp bạn rèn luyện kỹ năng, tự tin áp dụng trong học tập và ôn thi THPT Quốc gia.
A. Phương pháp tính tích vô hướng của hai vectơ
- Bước 1. Xác định góc giữa hai vectơ
- Bước 2. Dùng hệ thức lượng trong tam giác tìm độ dài vectơ
- Bước 3. Dùng định nghĩa tích vô hướng hai vectơ
![]() \(\overrightarrow{a}.\overrightarrow{b} =
\left| \overrightarrow{a} \right|\left| \overrightarrow{b}
\right|.cos(\overrightarrow{a},\overrightarrow{b})\)
\(\overrightarrow{a}.\overrightarrow{b} =
\left| \overrightarrow{a} \right|\left| \overrightarrow{b}
\right|.cos(\overrightarrow{a},\overrightarrow{b})\)
B. Ví dụ minh họa tính tích vô hướng của hai vectơ
Ví dụ 1: Tìm điều kiện của ![]() \(\overrightarrow{u},\overrightarrow{v}\) để:
\(\overrightarrow{u},\overrightarrow{v}\) để:
a) ![]() \(\overrightarrow{u}.\overrightarrow{v}
= \left| \overrightarrow{u} \right|.\left| \overrightarrow{v}
\right|\). b)
\(\overrightarrow{u}.\overrightarrow{v}
= \left| \overrightarrow{u} \right|.\left| \overrightarrow{v}
\right|\). b) ![]() \(\overrightarrow{u}.\overrightarrow{v} = - \left|
\overrightarrow{u} \right|.\left| \overrightarrow{v}
\right|\).
\(\overrightarrow{u}.\overrightarrow{v} = - \left|
\overrightarrow{u} \right|.\left| \overrightarrow{v}
\right|\).
Hướng dẫn giải
a) Ta có ![]() \(\overrightarrow{u}.\overrightarrow{v} =
|\overrightarrow{u}|.|\overrightarrow{v}|cos\left(
\overrightarrow{u},\overrightarrow{v} \right)\).
\(\overrightarrow{u}.\overrightarrow{v} =
|\overrightarrow{u}|.|\overrightarrow{v}|cos\left(
\overrightarrow{u},\overrightarrow{v} \right)\).
Do đó để ![]() \(\overrightarrow{u}.\overrightarrow{v} =
|\overrightarrow{u}|.|\overrightarrow{v}|\) thì
\(\overrightarrow{u}.\overrightarrow{v} =
|\overrightarrow{u}|.|\overrightarrow{v}|\) thì ![]() \(\cos\left( \overrightarrow{u},\overrightarrow{v}
\right) = 1\) hay
\(\cos\left( \overrightarrow{u},\overrightarrow{v}
\right) = 1\) hay ![]() \(\left(
\overrightarrow{u},\overrightarrow{v} \right) = 0^{0}\) nên
\(\left(
\overrightarrow{u},\overrightarrow{v} \right) = 0^{0}\) nên ![]() \(\overrightarrow{u},\overrightarrow{v}\) cùng hướng.
\(\overrightarrow{u},\overrightarrow{v}\) cùng hướng.
b) Ta có ![]() \(\overrightarrow{u}.\overrightarrow{v} =
|\overrightarrow{u}|.|\overrightarrow{v}|cos\left(
\overrightarrow{u},\overrightarrow{v} \right)\).
\(\overrightarrow{u}.\overrightarrow{v} =
|\overrightarrow{u}|.|\overrightarrow{v}|cos\left(
\overrightarrow{u},\overrightarrow{v} \right)\).
Do đó để ![]() \(\overrightarrow{u}.\overrightarrow{v} = -
|\overrightarrow{u}| \cdot \overrightarrow{v}|\) thì
\(\overrightarrow{u}.\overrightarrow{v} = -
|\overrightarrow{u}| \cdot \overrightarrow{v}|\) thì ![]() \(\cos\left( \overrightarrow{u},\overrightarrow{v}
\right) = - 1\) hay
\(\cos\left( \overrightarrow{u},\overrightarrow{v}
\right) = - 1\) hay ![]() \(\left(
\overrightarrow{u},\overrightarrow{v} \right) = 180^{0}\) nên
\(\left(
\overrightarrow{u},\overrightarrow{v} \right) = 180^{0}\) nên ![]() \(\overrightarrow{u},\overrightarrow{v}\) ngược hướng.
\(\overrightarrow{u},\overrightarrow{v}\) ngược hướng.
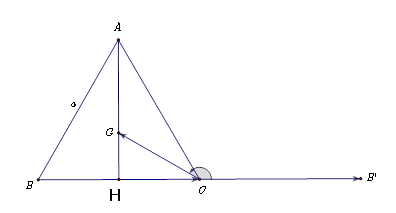
Ví dụ 2: Cho ![]() \(\Delta ABC\) đều cạnh
\(\Delta ABC\) đều cạnh ![]() \(a\), trọng tâm
\(a\), trọng tâm ![]() \(G\),
\(G\), ![]() \(AH\) là đường cao. Tính
\(AH\) là đường cao. Tính
a) ![]() \(\overrightarrow{AB\
}.\overrightarrow{AC\ }\) b)
\(\overrightarrow{AB\
}.\overrightarrow{AC\ }\) b) ![]() \(\overrightarrow{AH}.\overrightarrow{BC}\) c)
\(\overrightarrow{AH}.\overrightarrow{BC}\) c) ![]() \(\overrightarrow{BC}.\overrightarrow{CG}\)
\(\overrightarrow{BC}.\overrightarrow{CG}\)
Hướng dẫn giải
a) Ta có:
![]() \(\overrightarrow{AB\
}.\overrightarrow{AC\ } = \left| \overrightarrow{AB\ } \right|.\left|
\overrightarrow{AC\ } \right|.cos\left( \overrightarrow{AB\
},\overrightarrow{AC\ } \right)\)
\(\overrightarrow{AB\
}.\overrightarrow{AC\ } = \left| \overrightarrow{AB\ } \right|.\left|
\overrightarrow{AC\ } \right|.cos\left( \overrightarrow{AB\
},\overrightarrow{AC\ } \right)\)
![]() \(= AB.AC.cos60{^\circ} = a.a.\frac{1}{2} =
\frac{1}{2}a^{2}\).
\(= AB.AC.cos60{^\circ} = a.a.\frac{1}{2} =
\frac{1}{2}a^{2}\).
b) Ta có: ![]() \(\overrightarrow{AH}.\overrightarrow{BC} =
AH.BC.cos90^{0} = 0\)
\(\overrightarrow{AH}.\overrightarrow{BC} =
AH.BC.cos90^{0} = 0\)
c) Ta có:
![]() \(AH = \sqrt{AB^{2} - BH^{2}} = \sqrt{a^{2}
- \left( \frac{a}{2} \right)^{2}} = \frac{a\sqrt{3}}{2}\)
\(AH = \sqrt{AB^{2} - BH^{2}} = \sqrt{a^{2}
- \left( \frac{a}{2} \right)^{2}} = \frac{a\sqrt{3}}{2}\)
![]() \(AG = \frac{2}{3}AH =
\frac{2}{3}.\frac{a\sqrt{3}}{2} = \frac{a\sqrt{3}}{3}.\)
\(AG = \frac{2}{3}AH =
\frac{2}{3}.\frac{a\sqrt{3}}{2} = \frac{a\sqrt{3}}{3}.\)
 \(\overrightarrow{BC}.\overrightarrow{CG}
= \left| \overrightarrow{BC} \right|.\left| \overrightarrow{CG}
\right|.cos\left( \widehat{\overrightarrow{BC},\overrightarrow{CG}}
\right) = BC.CG.cos\left(
\widehat{\overrightarrow{CB'},\overrightarrow{CG}}
\right)\)
\(\overrightarrow{BC}.\overrightarrow{CG}
= \left| \overrightarrow{BC} \right|.\left| \overrightarrow{CG}
\right|.cos\left( \widehat{\overrightarrow{BC},\overrightarrow{CG}}
\right) = BC.CG.cos\left(
\widehat{\overrightarrow{CB'},\overrightarrow{CG}}
\right)\)
![]() \(= BC.CG.cos150^{0} =
a.\frac{a\sqrt{3}}{3}.\left( - \frac{\sqrt{3}}{2} \right) = -
\frac{a^{2}}{2}\)
\(= BC.CG.cos150^{0} =
a.\frac{a\sqrt{3}}{3}.\left( - \frac{\sqrt{3}}{2} \right) = -
\frac{a^{2}}{2}\)
Ví dụ 3: Cho tam giác ![]() \(ABC\) vuông tại
\(ABC\) vuông tại ![]() \(A\) có
\(A\) có ![]() \(AB = a\),
\(AB = a\), ![]() \(AC =
a\sqrt{3}\) và
\(AC =
a\sqrt{3}\) và ![]() \(AM\) là trung tuyến. Tính tích vô hướng
\(AM\) là trung tuyến. Tính tích vô hướng ![]() \(\overrightarrow{BA}.\overrightarrow{AM}\).
\(\overrightarrow{BA}.\overrightarrow{AM}\).
Hướng dẫn giải
Ta có:
![]() \(AM = \frac{1}{2}BC =
\frac{1}{2}\sqrt{AB^{2} + AC^{2}} = a\)
\(AM = \frac{1}{2}BC =
\frac{1}{2}\sqrt{AB^{2} + AC^{2}} = a\)
![]() \(AB = AM = BM = a \Leftrightarrow \Delta
ABM\) đều
\(AB = AM = BM = a \Leftrightarrow \Delta
ABM\) đều
![]() \(\Rightarrow \cos\widehat{BAM} = cos60^{0}
= \frac{1}{2}\)
\(\Rightarrow \cos\widehat{BAM} = cos60^{0}
= \frac{1}{2}\)
Khi đó: ![]() \(\overrightarrow{BA}.\overrightarrow{AM} = -
\overrightarrow{AB}.\overrightarrow{AM} = - AB.AM.cosA = -
a.a.\frac{1}{2} = - \frac{a^{2}}{2}\).
\(\overrightarrow{BA}.\overrightarrow{AM} = -
\overrightarrow{AB}.\overrightarrow{AM} = - AB.AM.cosA = -
a.a.\frac{1}{2} = - \frac{a^{2}}{2}\).
Ví dụ 4: Cho tam giác ![]() \(ABC\) vuông tại
\(ABC\) vuông tại ![]() \(B\),
\(B\), ![]() \(BC = a\sqrt{3}\). Tính
\(BC = a\sqrt{3}\). Tính ![]() \(\overrightarrow{AC}.\overrightarrow{CB}\).
\(\overrightarrow{AC}.\overrightarrow{CB}\).
Hướng dẫn giải
Hình vẽ minh họa:
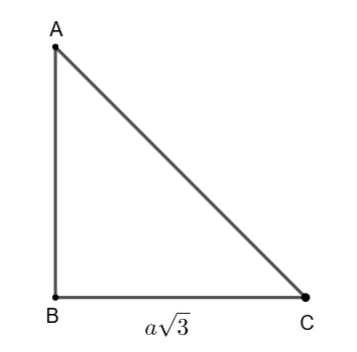
Ta có:
![]() \(\overrightarrow{AC}.\overrightarrow{CB}
= \left| \overrightarrow{AC} \right|\left| \overrightarrow{CB}
\right|.cos\left( \overrightarrow{AC},\overrightarrow{CB}
\right)\)
\(\overrightarrow{AC}.\overrightarrow{CB}
= \left| \overrightarrow{AC} \right|\left| \overrightarrow{CB}
\right|.cos\left( \overrightarrow{AC},\overrightarrow{CB}
\right)\)
![]() \(= \left| \overrightarrow{AC}
\right|\left| \overrightarrow{CB} \right|.cos\left( 180{^\circ} -
\widehat{C} \right)\)
\(= \left| \overrightarrow{AC}
\right|\left| \overrightarrow{CB} \right|.cos\left( 180{^\circ} -
\widehat{C} \right)\)
![]() \(= - \left| \overrightarrow{AC}
\right|\left| \overrightarrow{CB} \right|.cos\widehat{C} = - \left|
\overrightarrow{AC} \right|\left| \overrightarrow{CB}
\right|.\frac{BC}{AC} = - BC^{2} = - 3a^{2}\).
\(= - \left| \overrightarrow{AC}
\right|\left| \overrightarrow{CB} \right|.cos\widehat{C} = - \left|
\overrightarrow{AC} \right|\left| \overrightarrow{CB}
\right|.\frac{BC}{AC} = - BC^{2} = - 3a^{2}\).
C. Bài tập tự rèn luyện có đáp án chi tiết
Bài tập 1: Cho tam giác ![]() \(ABC\) , có
\(ABC\) , có ![]() \(AB = 2,\ AC = 3,\ \widehat{BAC} =
60^{0}\) Gọi
\(AB = 2,\ AC = 3,\ \widehat{BAC} =
60^{0}\) Gọi ![]() \(M\) là trung điểm của đoạn thẳng
\(M\) là trung điểm của đoạn thẳng ![]() \(BC\). Điểm
\(BC\). Điểm ![]() \(D\) thỏa mãn
\(D\) thỏa mãn ![]() \(\overrightarrow{AD} =
\frac{7}{12}\overrightarrow{AC}\).
\(\overrightarrow{AD} =
\frac{7}{12}\overrightarrow{AC}\).
a) Tìm ![]() \(\overrightarrow{AB}.\overrightarrow{AC}\). b) Tính
\(\overrightarrow{AB}.\overrightarrow{AC}\). b) Tính ![]() \(\overrightarrow{AM}.\overrightarrow{BD}\). c) Chứng minh
\(\overrightarrow{AM}.\overrightarrow{BD}\). c) Chứng minh ![]() \(AM\bot BD\).
\(AM\bot BD\).
Bài tập 2. Cho tam giác đểu ![]() \(ABC\), có
\(ABC\), có ![]() \(AB = 2\)
\(AB = 2\)
a) Gọi ![]() \(M\) là trung điểm của đoạn thẳng
\(M\) là trung điểm của đoạn thẳng ![]() \(BC\). Tính
\(BC\). Tính ![]() \(\overrightarrow{MA}.\overrightarrow{BC}\);
\(\overrightarrow{MA}.\overrightarrow{BC}\); ![]() \(\overrightarrow{MA}.\overrightarrow{AC}\).
\(\overrightarrow{MA}.\overrightarrow{AC}\).
b) Gọi ![]() \(N\) là điểm đối xứng của
\(N\) là điểm đối xứng của ![]() \(B\) qua
\(B\) qua ![]() \(C\). Tính tích vô hướng
\(C\). Tính tích vô hướng ![]() \(\overrightarrow{AM}.\overrightarrow{AN}\).
\(\overrightarrow{AM}.\overrightarrow{AN}\).
c) Lấy ![]() \(P\) thuộc đoan
\(P\) thuộc đoan ![]() \(AN\) sao cho
\(AN\) sao cho ![]() \(AP
= 3PN\). Hãy biểu thị
\(AP
= 3PN\). Hãy biểu thị ![]() \(\overrightarrow{AP},\ \
\overrightarrow{MP}\) theo hai vectơ
\(\overrightarrow{AP},\ \
\overrightarrow{MP}\) theo hai vectơ ![]() \(\overrightarrow{AB}\ \\)và
\(\overrightarrow{AB}\ \\)và ![]() \(\overrightarrow{AC}\). Tính độ dài
\(\overrightarrow{AC}\). Tính độ dài ![]() \(MP.\)
\(MP.\)
Bài tập 3: Cho tam giác ![]() \(ABC\) vuông tại
\(ABC\) vuông tại ![]() \(A\) có
\(A\) có ![]() \(AB = a,\ \ BC = 2a\) và
\(AB = a,\ \ BC = 2a\) và ![]() \(G\) là trọng tâm.
\(G\) là trọng tâm.
a) Tính các tích vô hướng: ![]() \(\overrightarrow{BA}.\overrightarrow{BC}\);
\(\overrightarrow{BA}.\overrightarrow{BC}\); ![]() \(\overrightarrow{BC}.\overrightarrow{CA}\).
\(\overrightarrow{BC}.\overrightarrow{CA}\).
b) Tính giá trị của biểu thức ![]() \(\overrightarrow{AB}.\overrightarrow{BC} +
\overrightarrow{BC}.\overrightarrow{CA} +
\overrightarrow{CA}.\overrightarrow{AB}\).
\(\overrightarrow{AB}.\overrightarrow{BC} +
\overrightarrow{BC}.\overrightarrow{CA} +
\overrightarrow{CA}.\overrightarrow{AB}\).
c) Tính giá trị của biểu thức ![]() \(\overrightarrow{GA}.\overrightarrow{GB} +
\overrightarrow{GB}.\overrightarrow{GC} +
\overrightarrow{GC}.\overrightarrow{GA}\).
\(\overrightarrow{GA}.\overrightarrow{GB} +
\overrightarrow{GB}.\overrightarrow{GC} +
\overrightarrow{GC}.\overrightarrow{GA}\).
Bạn muốn xem toàn bộ tài liệu? Hãy nhấn Tải về ngay!
--------------------------------------------------
Qua bài viết Bài tập tích vô hướng của hai vectơ Toán 10 có đáp án chi tiết dễ hiểu, bạn đã được củng cố toàn bộ kiến thức trọng tâm về tích vô hướng, công thức tính, và các dạng bài thường gặp. Việc luyện tập thường xuyên với chuyên đề tích vô hướng của hai vectơ có đáp án sẽ giúp bạn nâng cao khả năng tư duy hình học, ghi nhớ nhanh công thức và đạt điểm cao trong các bài kiểm tra, kỳ thi Toán 10.









