Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Tìm M thuộc d sao cho MA+MB nhỏ nhất Toán 10

Chuyên đề Phương trình đường thẳng

Bài trước

Tải về

Bài sau

Lớp: Lớp 10

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Tìm điều kiện để tổng khoảng cách MA + MB nhỏ nhất

Trong chuyên đề Phương trình đường thẳng – Toán 10, dạng bài tìm điểm M thuộc đường thẳng d sao cho MA + MB nhỏ nhất là dạng toán quen thuộc nhưng đòi hỏi học sinh hiểu bản chất hình học để xử lý nhanh và chính xác. Bài viết này sẽ hướng dẫn bạn phương pháp giải tối ưu dựa trên tính chất phản xạ, định lý đường thẳng ngắn nhất, cùng các bước trình bày rõ ràng giúp bạn nắm chắc kỹ thuật và áp dụng vào mọi dạng bài liên quan.

Ví dụ 1: Trong mặt phẳng tọa độ Oxy cho Δ: x - y + 1 = 0 và hai điểm A(2; 1), B(9; 6). Điểm M(a; b) nằm trên đường Δ sao cho MA + MB nhỏ nhất. Tính giá trị của biểu thức a + b.

Hướng dẫn giải

Gọi A' đối xứng A qua d ta có A'(0; 3) khi đó điểm $M = A'B \cap d$

Tìm được M(3; 4).

Ví dụ 2. Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d: x - 4y + 15 = 0 và điểm A(0; 2). Tìm tọa độ điểm M thuộc d để đoạn AM có độ dài nhỏ nhất.

Hướng dẫn giải

Điểm $M \in d\ \Leftrightarrow M(4t - 15;t)$

Ta có: $AM = \sqrt{(4t - 17)^{2} + t^{2}} = \sqrt{17\left( t^{2} - 8t + 17 \right)}$

$= \sqrt{17\left\lbrack (t - 4)^{2} + 1 \right\rbrack} \geq \sqrt{17}$ , $\forall t\mathbb{\in R}$ .

$\Rightarrow \min AM = \sqrt{17}$ , đạt được tại t = 4. Khi đó M(1; 4).

Ví dụ 3: Cho 3 điểm A(-6; 3), B(0; -1), C(3; 2). Tìm M trên đường thẳng d: 2x - y - 3 = 0 mà biểu thức $\left| \overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC} \right|$ đạt giá trị nhỏ nhất?

Hướng dẫn giải

Cách 1:

Tìm tọa độ điểm I(x; y) sao cho $\overrightarrow{IA} + \overrightarrow{IB} + \overrightarrow{IC} = \overrightarrow{0}$ . Suy ra $I\left( - 1;\frac{4}{3} \right)$

Ta có: $\overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC} = 3\overrightarrow{MI} + \overrightarrow{IA} + \overrightarrow{IB} + \overrightarrow{IC}$

$\left| \overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC} \right| = 3\left| \overrightarrow{MI} \right|$ .

Vậy $\left| \overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC} \right|$ nhỏ nhất khí $\left| \overrightarrow{MI} \right|$ nhỏ nhất.

$\left| \overrightarrow{MI} \right|$ nhỏ nhất khi M là hình chiếu vuông góc của I xuống đường thẳng d.

Đường thẳng d' đi qua I và vuông góc với d có phương trình: $x + 2y = \frac{5}{3}$

M là giao điểm của d và d' nên M là nghiệm của hệ: $\left\{ \begin{matrix} 2x - y = 3 \\ x + 2y = \frac{5}{3} \end{matrix} \right.\ \Rightarrow M\left( \frac{- 13}{15};\frac{19}{15} \right)$

Cách 2:

thuộc suy ra

$\overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC} = ( - 3 - 3t; - 6t - 5)$

$\left| \overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC} \right| = \sqrt{( - 3 - 3t)^{2 +} + ( - 6 - 5t)^{2}}$

$\left| \overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC} \right| = \sqrt{45t^{2} + 78t + 34} = \sqrt{45\left( t + \frac{13}{15} \right)^{2} + \frac{1}{5}}$

$\left| \overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC} \right|$ nhỏ nhất khi $t = - \frac{13}{15}$ . Suy ra $M\left( \frac{- 13}{15};\frac{19}{15} \right)$ .

Ví dụ 4. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có đỉnh A(2; 2), B(1; -3), C(-2; 2). Điểm M thuộc trục tung sao cho $\left| \overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC} \right|$ nhỏ nhất có tung độ là?

Hướng dẫn giải

Gọi G(a; b) là trọng tâm tam giác ABC.

Suy ra $\left\{ \begin{matrix}a = \dfrac{x_{A} + x_{B} + x_{C}}{3} \\b = \dfrac{y_{A} + y_{B} + y_{C}}{3}\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}a = \dfrac{2 + 1 - 2}{3} \\b = \dfrac{2 - 3 + 2}{3}\end{matrix} \right.$

$\Leftrightarrow \left\{ \begin{matrix}a = \frac{1}{3} \\b = \frac{1}{3}\end{matrix} \right.\ \Rightarrow G\left( \frac{1}{3};\frac{1}{3}\right)$ .

Ta có:

$\left| \overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC} \right| = \left| \overrightarrow{MG} + \overrightarrow{GA} + \overrightarrow{MG} + \overrightarrow{GB} + \overrightarrow{MG} + \overrightarrow{GC} \right|$ $= \left| 3\overrightarrow{MG} \right| = 3MG$ .

Suy ra $\left| \overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC} \right|$ nhỏ nhất khi MG nhỏ nhất.

Mặt khác M thuộc trục tung nên MG nhỏ nhất khi M là hình chiếu của G lên trục tung.

Vậy $M\left( 0;\frac{1}{3} \right)$ .

Ví dụ 5: Trong mặt phẳng tọa độ Oxy cho Δ: x - y + 1 = 0 và hai điểm A(2; 1), B(9; 9). Điểm M(a; b) nằm trên đường Δ sao cho MA + MB nhỏ nhất. Tính a + b ta được kết quả là

Hướng dẫn giải

Gọi A’ là điểm đối xứng của A qua đường thẳng Δ.

Hình vẽ minh họa như sau:

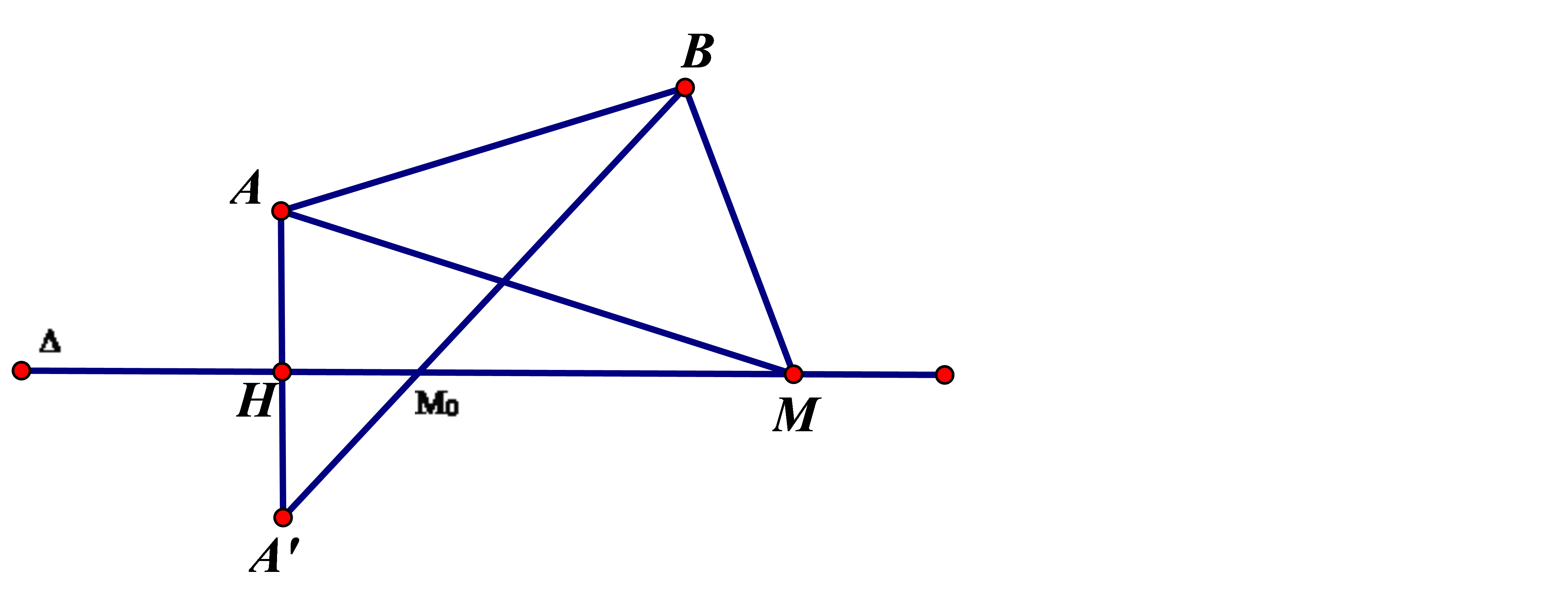
Ta có:

$MA + MB = MA' + MB \geq A'B$

Đẳng thức xảy ra $\Leftrightarrow$ M trùng với M₀ (M₀ là giao điểm của Δ và A’B)

Ta có: $AA'\bot\Delta$ nên $\overrightarrow{n_{AA'}} = \overrightarrow{a_{\Delta}} = (1;1)$

(AA'):x + y - 3 = 0

Gọi $H = AA' \cap \Delta \Rightarrow H(1;2)$

Vì A’ đối xứng với A qua Δ nên H là trung điểm AA’

$\Rightarrow A'(0;3)$

Đường thẳng A’B qua B có VTCP $\overrightarrow{A'B} = (9;3) = 3(3;1) \Rightarrow \overrightarrow{n_{A'B}} = (1; - 3)$

=> A'B: x - 3y + 9 = 0

Tọa độ M₀ thỏa hệ:

$\left\{ \begin{matrix} x - y + 1 = 0 \\ x - 3y + 9 = 0 \end{matrix} \right.\ \Leftrightarrow M_{0}(3;4)$ =>M(3; 4). Vậy a + b = 7.

Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu.

-------------------------------------

Gợi ý tài liệu tham khảo:

Qua bài viết, bạn đã biết cách giải dạng toán tìm M thuộc d để MA + MB đạt giá trị nhỏ nhất bằng phương pháp phản xạ và hình học giải tích. Đây là dạng bài trọng tâm trong chương Phương trình đường thẳng, xuất hiện nhiều trong kiểm tra, đánh giá năng lực và đề thi học kỳ. Hãy luyện thêm bài tập để thành thạo phương pháp và đạt điểm cao môn Toán 10. Chúc bạn học tốt!

Tải về

Chọn file muốn tải về: