Tìm tọa độ hình chiếu, điểm đối xứng qua đường thẳng
Cách tìm tọa độ hình chiếu, đường đối xứng
Việc tìm tọa độ hình chiếu và điểm đối xứng qua đường thẳng là kỹ năng quan trọng trong phương pháp tọa độ mặt phẳng. Bài viết này giúp bạn nắm chắc công thức, cách làm nhanh và các dạng bài Toán 10 thường gặp, hỗ trợ học tốt và giải bài chính xác.
A. Ví dụ minh họa tìm tọa độ hình chiếu, điểm đối xứng
Ví dụ: Trong mặt phẳng 
\(Oxy\) cho điểm \(M(2;\ 1)\) và đường thẳng \(d:x - y + 2 = 0\)
a) Tìm tọa độ hình chiếu \(H\)của \(M\) trên \(d.\)
b) Tìm tọa độ điểm \(M'\) đối xứng với \(M\) qua \(d.\)
Hướng dẫn giải
Hình vẽ minh họa:
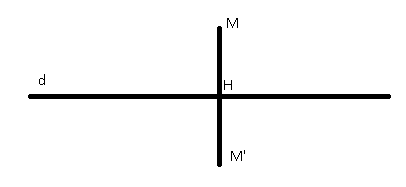
a) Vì HM vuông góc \(d:x - y + 2 =
0\) nên nhận \(\overrightarrow{n} =
(1;1)\)làm vectơ pháp tuyến và HM đi qua \(M(2;\ 1)\) nên phương trình của HM: \(1(x - 2) + 1(y - 1) = 0 \Leftrightarrow x + y - 3
= 0.\)
H là giao điểm của HM và \(d\)nên tọa độ H là nghiệm của hệ phương trình:
\(\left\{ \begin{matrix}
x - y = - 2 \\
x + y = 3
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
x = \frac{1}{2} \\
y = \frac{5}{2}
\end{matrix} \right.\).
Vậy \(H(\frac{1}{2};\frac{5}{3})\)
b) Vì \(M'\) đối xứng với \(M\)qua \(d\) nên H là trung điểm MM’. Do đó:
\(\left\{ \begin{matrix}
x_{M'} = 2x_{H} - x_{M} \\
y_{M'} = 2y_{H} - y_{M}
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
x_{M'} = 2.\frac{1}{2} - 2 \\
y_{M'} = 2.\frac{5}{2} - 1
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
x = - 1 \\
y = 4
\end{matrix} \right.\).
Vậy \(M'( - 1;4).\)
B. Bài tập vận dụng có hướng dẫn chi tiết
Câu 1: Trong mặt phẳng tọa độ \(Oxy\), hình chiếu vuông góc của điểm \(A(2;1)\) lên đường thẳng \(d\): \(2x + y - 7
= 0\) có tọa độ là:
A. \(\left( \frac{14}{5};\frac{7}{5}
\right)\). B. \(\left( - \frac{14}{5};
- \frac{7}{5} \right)\). C. \((3;1)\). D. \(\left( \frac{5}{3};\frac{3}{2}
\right)\).
Câu 2: Cho đường thẳng \(d: - 3x + y - 3 =
0\) và điểm \(N( - 2;4)\). Tọa độ hình chiếu vuông góc của \(N\) trên \(d\) là:
A. \(( - 3; - 6)\). B. \(\left( - \frac{1}{3};\frac{11}{3}
\right)\). C. \(\left(
\frac{2}{5};\frac{21}{5} \right)\). D. \(\left( \frac{1}{10};\frac{33}{10}
\right)\).
Câu 3: Cho điểm \(M(1;2)\) và đường thẳng \(d:2x + y - 5 = 0\). Tọa độ của điểm đối xứng với điểm \(M\) qua \(d\) là:
A. \(\left( \frac{9}{5};\frac{12}{5}
\right)\). B. \(( - 2;6)\). C. \(\left( 0;\frac{3}{2} \right)\). D. \((3; - 5)\).
Đáp án bài tập có trong file tải, mời bạn đọc tải tài liệu tham khảo đầy đủ!
--------------------------------
Qua các ví dụ và công thức đã trình bày, bạn có thể dễ dàng giải được bài toán hình chiếu và điểm đối xứng trong mặt phẳng tọa độ. Hãy lưu lại bài viết để ôn tập và vận dụng hiệu quả trong các bài kiểm tra Toán 10.
