Tổng hợp kiến thức Vectơ trong mặt phẳng tọa độ
Vectơ trong mặt phẳng tọa độ Oxy Toán 10
Trong chương trình Toán 10, chuyên đề Vectơ trong mặt phẳng tọa độ Oxy là nền tảng quan trọng giúp học sinh làm chủ các kiến thức hình học và đại số. Bài viết này sẽ giúp bạn tổng hợp toàn bộ kiến thức về vectơ, từ định nghĩa, quy tắc, công thức tọa độ vectơ cho đến các ví dụ minh họa và bài tập vận dụng. Cùng khám phá chi tiết để nắm vững chuyên đề Vectơ trong mặt phẳng tọa độ – bước đệm quan trọng cho các bài toán tọa độ phức tạp hơn ở lớp 11 và ôn thi THPT Quốc gia.
A. Định nghĩa
Hệ trục tọa độ gồm hai trục vuông góc 
\(Ox\) và \(Oy\) với hai vectơ đơn vị lần lượt là \(\overrightarrow{i},\ \overrightarrow{j}\). Điểm O gọi là gốc tọa độ, \(Ox\) gọi là trục hoành và \(Oy\) gọi là trục tung.
Kí hiệu \(Oxy\) hay \(\left( O;\overrightarrow{i},\overrightarrow{j}
\right)\)
B. Tọa độ điểm, tọa độ vectơ
Trong hệ trục tọa độ \(\left(
O;\overrightarrow{i},\overrightarrow{j} \right)\) nếu \(\overrightarrow{u} = x\overrightarrow{i} +
y\overrightarrow{j}\) thì cặp số \((x;y)\) được gọi là tọa độ của vectơ \(\overrightarrow{u}\), kí hiệu là \(\overrightarrow{u} = (x;y)\) hay \(\overrightarrow{u}(x;y)\).
x được gọi là hoành độ, y được gọi là tung độ của vectơ \(\overrightarrow{u}\)
Trong hệ trục tọa độ \(\left(
O;\overrightarrow{i},\overrightarrow{j} \right)\), tọa độ của vectơ \(\overrightarrow{OM}\) gọi là tọa độ của điểm M, kí hiệu là \(M =
(x;y)\) hay \(M(x;y)\). x được gọi là hoành độ, y được gọi là tung độ của điểm M.
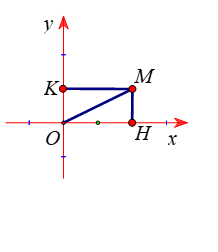
Nhận xét: Gọi H, K lần lượt là hình chiếu của M lên \(Ox\) và \(Oy\) (như hình vẽ phần 1) thì
\(M(x;y)
\Leftrightarrow \overrightarrow{OM} = x\overrightarrow{i} +
y\overrightarrow{j} = \overrightarrow{OH} +
\overrightarrow{OK}\)
Như vậy \(\overrightarrow{OH} =
x\overrightarrow{i},\ \ \overrightarrow{OK} =
y\overrightarrow{j}\) hay \(x =
\overline{OH},\ \ y = \overline{OK}\)
C. Tọa độ trung điểm của đoạn thẳng. Tọa độ trọng tâm tam giác
Cho \(A(x_{A};y_{A}),B(x_{B};y_{B})\) và M là trung điểm AB.
Tọa độ trung điểm \(M\left(
x_{M};y_{M} \right)\) của đoạn thẳng AB là
\(x_{M} = \frac{x_{A} + x_{B}}{2},\ \ y_{M} =
\frac{y_{A} + y_{B}}{2}\)
Cho tam giác \(ABC\) có \(A(x_{A};y_{A}),B(x_{B};y_{B}),\ \ C\left(
x_{C};y_{C} \right)\).
Tọa độ trọng tâm \(G\left( x_{G};y_{G} \right)\) của tam giác \(ABC\) là
\(x_{G} = \frac{x_{A} + x_{B} + x_{C}}{3}\) và \(y_{G} = \frac{y_{A} + y_{B} +
y_{C}}{2}\)
D. Biểu thức tọa độ của các phép toán vectơ
Cho \(\overrightarrow{u} = (x;y)\) ;\(\overrightarrow{u'} =
(x';y')\) và số thực k. Khi đó ta có:
1) \(\overrightarrow{u} =
\overrightarrow{u'} \Leftrightarrow \left\{ \begin{matrix}
x = x' \\
y = y'
\end{matrix} \right.\)
2) \(\overrightarrow{u} \pm
\overrightarrow{v} = (x \pm x';y \pm y')\)
3) \(k.\overrightarrow{u} =
(kx;ky)\)
4) \(\overrightarrow{u'}\) cùng phương \(\overrightarrow{u}\)(\(\overrightarrow{u} \neq
\overrightarrow{0}\)) khi và chỉ khi có số k sao cho \(\left\{ \begin{matrix}
x' = kx \\
y' = ky
\end{matrix} \right.\)
5) Độ dài vectơ \(\left| \overrightarrow{u}
\right| = \sqrt{x^{2} + y^{2}}\)
6) Cho \(A(x_{A};y_{A}),B(x_{B};y_{B})\) thì \(\overrightarrow{AB} = \left( x_{B} - x_{A};y_{B} -
y_{A} \right)\)
\(AB = \left| \overrightarrow{AB} \right|
= \sqrt{(x_{B} - x_{A})^{2} + (y_{B} - y_{A})^{2}}\)
E. Các dạng bài toán thường gặp
Dạng 1. Tìm tọa độ của vectơ và các phép trên hệ trục tọa độ.
Dạng 2. Tìm m để hai vectơ cùng phương.
Dạng 3. Cách tìm tọa độ điểm, tọa độ vectơ trong mặt phẳng Oxy.
Dạng 4. Tìm tọa độ điểm M thuộc mặt phẳng Oxy sao cho ba điểm thẳng hàng.
--------------------------------------
Qua bài viết “Tổng hợp kiến thức Vectơ trong mặt phẳng tọa độ”, bạn đã được hệ thống lại toàn bộ nội dung cốt lõi, công thức tính nhanh và các quy tắc giải bài tập vectơ trong Oxy. Hãy luyện tập thường xuyên với ví dụ minh họa và bài tập Toán 10 để ghi nhớ công thức và áp dụng linh hoạt trong các đề thi. Đừng quên theo dõi các bài viết tiếp theo để cập nhật kiến thức Toán học THPT chuẩn nhất, dễ hiểu và hiệu quả nhất!
