Cách xác định tam giác ABC là tam giác gì từ điều kiện đã cho
Chuyên đề Toán 10: Hệ thức lượng trong tam giác - Có đáp án
Trong chương trình Toán 10, chuyên đề hệ thức lượng trong tam giác là phần kiến thức quan trọng giúp học sinh rèn luyện kỹ năng suy luận và áp dụng công thức vào thực tế. Một dạng bài tiêu biểu là yêu cầu “xác định tam giác ABC là tam giác gì từ điều kiện đã cho”. Dạng toán này đòi hỏi học sinh phải vận dụng linh hoạt các hệ thức lượng, công thức cạnh – góc để xác định được tam giác vuông, cân, đều hay nhọn tù. Bài viết dưới đây sẽ hướng dẫn chi tiết cách phân tích và giải dạng toán này, kèm theo ví dụ minh họa cụ thể giúp bạn nắm chắc kiến thức.
A. Công thức liên hệ giữa cạnh và góc trong tam giác
Cho tam giác ABC có các cạnh như hình vẽ:
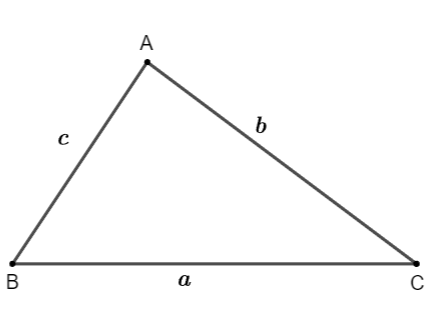
Tổng ba góc của tam giác
\(\widehat{A} +
\widehat{B} + \widehat{C} = 180^{0}\)
Định lý Pythagore
Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
\(\cos C = \frac{a^{2} + b^{2} -
c^{2}}{2ab};cosB = \frac{a^{2} + c^{2} - b^{2}}{2ac};cosA = \frac{b^{2}
+ c^{2} - a^{2}}{2bc}\)
\(\frac{a}{\sin A} = \frac{b}{\sin B} =
\frac{c}{\sin C} = 2R\) (với R là bán kính đường tròn ngoại tiếp tam giác ABC)
Công thức diện tích tam giác
\(S = \frac{1}{2}ab.sinC =
\frac{1}{2}bc.sinA = \frac{1}{2}ac.sinB\)
\(S = \frac{abc}{4r}\) (với r là bán kính đường tròn nội tiếp tam giác ABC)
\(S = \sqrt{p(p - a)(p - b)(p - c)};p =
\frac{a + b + c}{2}\).
B. Bài tập chứng minh dạng tam giác thỏa mãn điều kiện cho trước
Bài tập 1. Chứng minh rằng nếu tam giác ABC thoả mãn điều kiện: \(\frac{\sin A}{\sin B.cosC}\) = 2 thì tam giác ABC là tam giác cân.
Hướng dẫn giải
Hình vẽ minh họa
Ta có:
\(\frac{a}{\sin A} = \frac{b}{\sin B} =
\frac{c}{\sin C} = 2R\)
\(\Rightarrow \sin A = \frac{a}{2R};sinB =
\frac{b}{2R}\)
Lại có: \(\cos C = \frac{a^{2} + b^{2} -
c^{2}}{2ab}\)
Thay vào biểu thức đề bài cho ta được:
\(\frac{\sin A}{\sin B.cosC} = 2\Leftrightarrow \frac{\dfrac{a}{2R}}{\dfrac{b}{2R}.\dfrac{a^{2} + b^{2} -c^{2}}{2ab}} = 2\)
\(\Leftrightarrow
\frac{a}{2R}.\frac{2R.2ab}{b\left( a^{2} + b^{2} - c^{2} \right)} = 2
\Leftrightarrow \frac{a^{2}b}{b\left( a^{2} + b^{2} - c^{2} \right)} =
1\)
\(\Leftrightarrow a^{2} = a^{2} + b^{2} -
c^{2};(b \neq 0)\)
\(\Leftrightarrow b^{2} = c^{2}
\Leftrightarrow b = c\)
Vậy tam giác ABC cân tại A.
Bài tập 2. Tam giác ABC có đặc điểm gì nếu: \(\sin A = \frac{\sin B + 2sinC}{2cosB + \cos
C}\)?
Hướng dẫn giải
Hình vẽ minh họa
\(\sin A = \frac{\sin B + 2\sin C}{2\cos B +\cos C}\ \ \ \ (*)\)
Ta có:
\(\frac{a}{\sin A} = \frac{b}{\sin B} =
\frac{c}{\sin C} = 2R\)
\(\Rightarrow \sin A = \frac{a}{2R};\sin B =\frac{b}{2R};\sin C = \frac{c}{2R}\)
Lại có: \(\cos C = \frac{a^{2} + b^{2} -c^{2}}{2ab};\cos B = \frac{a^{2} + c^{2} - b^{2}}{2ac}\)
Ta có:
(*)\(\Leftrightarrow \dfrac{a}{2R} =\dfrac{\dfrac{b}{2R} + \dfrac{2c}{2R}}{2.\dfrac{a_{\ }^{2}\ + c^{2} -b^{2}}{2ac} + \dfrac{a_{\ }^{2}\ + b^{2} - c^{2}}{2ab}}\)
\(\Leftrightarrow a\left( \frac{a_{\
}^{2}\ + c^{2} - b^{2}}{ac} + \frac{a_{\ }^{2}\ + b^{2} - c^{2}}{2ab}
\right) = b + 2c\)
\(\Leftrightarrow (\frac{a_{\ }^{2}\ +
c^{2} - b^{2}}{c} - 2c) + (\frac{a_{\ }^{2}\ + b^{2} - c^{2}}{2b} - b)
= 0\)
\(\Leftrightarrow \frac{a^{2} - b^{2} -
c^{2}}{c} + \frac{a^{2} - b^{2} - c^{2}}{2b} = 0\)
\(\Leftrightarrow \left( a^{2} - b^{2} -
c^{2} \right).\left\lbrack \frac{1}{c} + \frac{1}{2b} \right\rbrack = 0
\Leftrightarrow a^{2} = b^{2} + c^{2}\)
Suy ra tam giác ABC vuông tại A.
Bài tập 3. Cho tam giác ABC có BC = a, AB = c, AC = b. Tam giác ABC có đặc điểm gì nếu: \(\frac{1 + \cos B}{\sin
B} = \frac{2a + c}{\sqrt{4a^{2} - c^{2}}}\)?
Hướng dẫn giải
Hình vẽ minh họa
Ta có: \(\frac{1 + \cos B}{\sin B} =
\frac{2a + c}{\sqrt{4a^{2} - c^{2}}}\ \ (*)\)
Nhận thấy cả hai vế của (*) đều dương nên bình phương hai vế ta có
\(\frac{(1 + \cos B)^{2}}{\sin^{2}B} =\frac{(2a + c)^{2}}{4a^{2} - c^{2}}\)
\(\Leftrightarrow \frac{(1 + \cos
B)^{2}}{1 - cos^{2}B} = \frac{(2a + c)^{2}}{(2a - c)(2a +
c)}\)
\(\Leftrightarrow \frac{1 + \cos B}{1 -
\cos B} = \frac{2a + c}{2a - c}\)\(\Leftrightarrow \frac{1 + \cos B}{1 -
\cos B} = \frac{2a + c}{2a - c}\)
\(\Leftrightarrow \frac{1 + \cos B}{2} =
\frac{2a + c}{4a}\)\(\Leftrightarrow \cos B =
\frac{c}{2a}\)
\(\Leftrightarrow 2ac\cos B =
c^{2}\)\(\Leftrightarrow a^{2} + c^{2} - b^{2} =
c^{2}\)
\(\Leftrightarrow a = b
\Leftrightarrow\) Tam giác ABC cân tại C.
----------------------------------------------------------------
Qua bài viết, chúng ta đã tìm hiểu phương pháp xác định tam giác ABC là tam giác gì dựa trên điều kiện cho trước, kết hợp sử dụng hệ thức lượng trong tam giác cùng các công thức quen thuộc về cạnh và góc. Đây là nền tảng quan trọng không chỉ phục vụ việc giải bài tập trong sách giáo khoa mà còn giúp bạn tự tin chinh phục các đề thi học kỳ và thi tuyển sinh.
Để học tốt chuyên đề này, học sinh cần:
-
Ghi nhớ các công thức hệ thức lượng trong tam giác.
-
Luyện tập nhiều dạng toán từ cơ bản đến nâng cao.
-
Biết cách phân loại tam giác dựa vào độ dài cạnh và mối quan hệ góc.
Việc học chắc chắn phần kiến thức này không chỉ hỗ trợ trong Toán 10 mà còn là hành trang vững chắc cho những chuyên đề lượng giác và hình học không gian ở các lớp sau.
