Bài tập nâng cao về tích của vectơ với một số có đáp án

Trong chương trình Toán 10, phần tích của vectơ với một số là kiến thức quan trọng giúp học sinh hiểu sâu về độ dài, hướng và mối quan hệ giữa các vectơ. Bài viết Bài tập nâng cao về tích của vectơ với một số có đáp án tổng hợp các dạng bài tập nâng cao, kèm hướng dẫn giải chi tiết và đáp án chính xác, giúp bạn củng cố kiến thức, rèn luyện kỹ năng và làm chủ chuyên đề Vectơ Toán 10 một cách hiệu quả.

Phần I. Bài tập vận dụng cao về tích của vectơ với một số

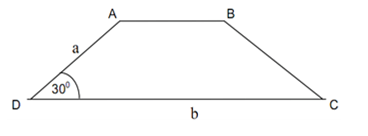
Bài tập 1: Cho hình thang cân ABCD có CD là đáy lớn, \(\widehat{ADC} = 30^{0}\) . Biết DA = a, DC = b, hãy biểu diễn \(\overrightarrow{DB}\) theo hai vectơ \(\overrightarrow{DA}\) và \(\overrightarrow{DC}\).

Bài tập 2 Cho tam giác \(ABC\), trên cạnh \(AC\) lấy điểm \(M\), trên cạnh \(BC\) lấy điểm \(N\) sao cho \(AM = 3MC\), \(NC = 2NB\). Gọi \(O\) là giao điểm của \(AN\) và \(BM\). Tính diện tích tam giác \(ABC\) biết diện tích tam giác \(OBN\) bằng 1.

Bài tập 3: Cho tam giác \(ABC\), gọi \(I\) là điểm trên \(BC\) kéo dài sao cho \(IB = 3IC\) . Gọi \(J,K\) lần lượt là những điểm trên cạnh \(AC,AB\) sao cho \(JA = 2JC;KB = 3KA\) . Khi đó \(\overrightarrow{BC} = m.\overrightarrow{AI} + n.\overrightarrow{JK}\) . Tính tổng \(P = m + n\) ?

Bài tập 4: Cho hình bình hành ABCD, lấy M trên cạnh AB và N trên cạnh CD sao cho \(\overrightarrow{AM} = \frac{1}{3}\overrightarrow{AB},\overrightarrow{DN} = \frac{1}{2}\overrightarrow{DC}\). Gọi I và J là các điểm thỏa mãn \(\overrightarrow{BI} = m\overrightarrow{BC},\overrightarrow{AJ} = n\overrightarrow{AI}\). Khi J là trọng tâm tam giác BMN thì tích m.n bằng bao nhiêu?

Bài tập 5: Cho tam giác ABC, trên cạnh AB lấ\(y\) điểm M, trên cạnh BC lấ\(y\) N sao cho AM=3MB, NC = 2BN. Gọi I là giao điểm của AN với CM. Tính diện tích tam giác ABC biết diện tích tam giác ICN bằng 2.

Bài tập 6: ∆ABC có trọng tâm G và hai điểm M, N thỏa mãn: \(3\overrightarrow{MA} - 2\overrightarrow{CM} = \overrightarrow{0}\), \(\overrightarrow{NA} - 2\overrightarrow{NB} = \overrightarrow{0}\). Chứng minh: \(\overrightarrow{NG} = 5\overrightarrow{GM}\).

Bài tập 7: Cho ∆ABC có M là trung điểm của BC, H là trực tâm, O là tâm đường tròn ngoại tiếp. Tìm \(x\) để \(\overrightarrow{HA} + \overrightarrow{HB} + \overrightarrow{HC} = x\overrightarrow{HO}\).

Bài tập 8: Cho tam giác \(ABC\) có \(AB = 3;\ \ AC = 4\). Gọi \(AD\) là đường phân giác trong của góc \(A\). Biết \(\overrightarrow{AD} = m\overrightarrow{AB} + n\overrightarrow{AC}\). Khi đó tổng \(m + n\) có giá trị là bao nhiêu?

Phần II. Đáp án bài tập vận dụng cao

Bài tập 1.

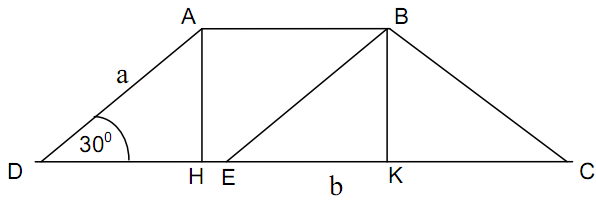
Kẻ BE // AD , E nằm trên cạnh CD. Ta có:

\(\overrightarrow{DB} = \overrightarrow{DA} + \overrightarrow{DE} =\overrightarrow{DA} + \frac{DE}{DC}\overrightarrow{DC} =\overrightarrow{DA} + \frac{DE}{DC}\overrightarrow{DC}\)

\(= \overrightarrow{DA} + \frac{DC -2KC}{DC}\overrightarrow{DC} = \overrightarrow{DA} + \frac{b -a\sqrt{3}}{b}\overrightarrow{DC}\).

Vậy \(\overrightarrow{DB} = \overrightarrow{DA} + \frac{b - a\sqrt{3}}{b}\overrightarrow{DC}.\)

Bài tập 2.

Hình vẽ minh họa:

Ta có: \(\overrightarrow{BO} = x\overrightarrow{BA} + (1 - x)\overrightarrow{BN}\) và \(\overrightarrow{AO} = y\overrightarrow{AM} + (1 - y)\overrightarrow{AB}\).

\(\Rightarrow \overrightarrow{AB} = y\overrightarrow{AM} + (x - y + 1)\overrightarrow{AB} + (x - 1)\overrightarrow{BN}\)

\(\Leftrightarrow (x - y)\overrightarrow{AB} + y\overrightarrow{AM} + (x - 1)\overrightarrow{BN} = \overrightarrow{0}\) (1)

Đặt \(\overrightarrow{CB} = \overrightarrow{a},\overrightarrow{CA} = \overrightarrow{b}\) ta được \(\overrightarrow{AB} = \overrightarrow{a} - \overrightarrow{b};\overrightarrow{AM} = - \frac{3}{4}\overrightarrow{b};\overrightarrow{BN} = - \frac{1}{3}\overrightarrow{a}\)

Thay vào (1) và thu gọn ta được:

\((x - y)\overrightarrow{a} - (x - y)\overrightarrow{b} = \frac{x - 1}{3}\overrightarrow{a} + \frac{3}{4}y\overrightarrow{b}\)

Suy ra \(\left\{ \begin{matrix}x - y = \dfrac{x - 1}{3} \\y - x = \dfrac{3}{4}y\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}x = \dfrac{1}{10} \\y = \dfrac{2}{5}\end{matrix} \right.\).

Với \(x = \frac{1}{10}\) ta được \(\overrightarrow{BO} = \frac{1}{10}\overrightarrow{BA} + \left( 1 - \frac{1}{10} \right)\overrightarrow{BN}\)

\(\Leftrightarrow \overrightarrow{BO} -\overrightarrow{BN} = \frac{1}{10}\left( \overrightarrow{BA} -\overrightarrow{BN} \right)\)

\(\Leftrightarrow \overrightarrow{NO} =\frac{1}{10}\overrightarrow{NA} \Leftrightarrow \frac{NA}{NO} =10\)

Vì \(S_{ONB} = 1 \Leftrightarrow S_{NAB} = 10 \Rightarrow S_{ABC} = 30\).

Không thể hiển thị hết nội dung tại đây — bấm Tải về để lấy toàn bộ tài liệu.

------------------------------------------

FAQ – Bài tập nâng cao về tích của vectơ với một số có đáp án

1. Tích của vectơ với một số là gì?

Tích của vectơ với một số là phép toán nhân một vectơ với một số thực để tạo ra một vectơ mới. Kết quả có thể làm thay đổi độ dài của vectơ và có thể đổi hướng nếu số nhân là số âm, trong khi phương của vectơ vẫn được giữ nguyên.

2. Sau khi nhân vectơ với một số thì những yếu tố nào thay đổi?

Khi thực hiện phép nhân vectơ với một số:

• Độ dài của vectơ thay đổi theo giá trị tuyệt đối của số nhân.
• Hướng của vectơ giữ nguyên nếu số nhân dương và ngược lại nếu số nhân âm.
• Phương của vectơ không thay đổi.

Đây là kiến thức quan trọng cần ghi nhớ khi giải các bài toán hình học vectơ.

3. Những dạng bài tập nâng cao về tích của vectơ với một số thường gặp là gì?

Các dạng bài phổ biến gồm:

• Tính tích của vectơ với một số.
• Chứng minh hai vectơ cùng phương.
• Xác định tọa độ vectơ sau phép nhân.
• Tìm hệ số để hai vectơ bằng nhau.
• Chứng minh đẳng thức vectơ.
• Giải bài toán hình học sử dụng phép nhân vectơ.

4. Làm thế nào để nhận biết hai vectơ là bội của nhau?

Hai vectơ là bội của nhau khi tồn tại một số thực sao cho vectơ này bằng số đó nhân với vectơ kia. Trong hình học tọa độ, điều này thường được kiểm tra thông qua tỉ số giữa các tọa độ tương ứng.

5. Vì sao cần học chuyên đề tích của vectơ với một số?

Đây là kiến thức nền tảng của chương Vectơ trong Toán 10, giúp học sinh giải quyết các bài toán về cùng phương, trung điểm, trọng tâm, chia đoạn thẳng theo tỉ số và chuẩn bị cho các chuyên đề tọa độ trong mặt phẳng.

--------------------------------------------

Qua bài viết này, bạn đã được luyện tập với nhiều bài tập nâng cao về tích của vectơ với một số kèm lời giải chi tiết, giúp củng cố và mở rộng kiến thức trong chuyên đề Vectơ Toán 10. Việc rèn luyện thường xuyên các dạng bài nâng cao sẽ giúp bạn tăng tốc độ làm bài, phát triển tư duy hình học và đạt điểm cao trong các kỳ thi.

👉 Hãy tiếp tục ôn luyện thêm các bài tập vectơ có đáp án chi tiết khác để hoàn thiện kỹ năng và chinh phục mọi dạng bài trong chương trình Toán 10.