Chứng minh đẳng thức vectơ về tích vô hướng Toán 10
Chứng minh đẳng thức vectơ trong Toán 10
Trong chương trình Toán 10, phần tích vô hướng của hai vectơ là kiến thức quan trọng giúp học sinh hiểu sâu về mối quan hệ giữa vectơ và góc tạo bởi chúng. Bài viết Chứng minh đẳng thức vectơ về tích vô hướng Toán 10 sẽ giúp bạn nắm vững cách vận dụng công thức tích vô hướng, thực hiện các bước chứng minh logic, đồng thời củng cố tư duy hình học và đại số thông qua các ví dụ minh họa dễ hiểu. Đây là nội dung nằm trong chuyên đề Tích vô hướng lớp 10, phù hợp cho ôn tập và luyện thi THPT Quốc gia.
A. Phương pháp chứng minh đẳng thức
- Nếu trong đẳng thức chứa bình phương độ dài của đoạn thẳng thì ta chuyển về vectơ nhờ đẳng thức
\(AB^{2} =
{\overrightarrow{AB}}^{2}\) - Sử dụng các tính chất của tích vô hướng, các quy tắc phép toán vectơ
- Sử dụng hằng đẳng thức vectơ về tích vô hướng.
B. Ví dụ minh họa chứng minh đẳng thức vectơ về tích vô hướng
Ví dụ 1: Cho tam giác \(ABC\) . Chứng minh rằng: \(AB^{2} +
\overrightarrow{AB}.\overrightarrow{BC} +
\overrightarrow{AB}.\overrightarrow{CA} = 0\)
Hướng dẫn giải
Hình vẽ minh họa:
Ta có
\(AB^{2} +
\overrightarrow{AB}.\overrightarrow{BC} +
\overrightarrow{AB}.\overrightarrow{CA} = AB^{2} +
\overrightarrow{AB}.(\overrightarrow{BC} +
\overrightarrow{CA})\)
\(= AB^{2} +
\overrightarrow{AB}.\overrightarrow{BA} = AB^{2} +
AB.BA.cos180^{0}\)
\(= AB^{2} - AB^{2} = 0\)
Vậy \(AB^{2} +
\overrightarrow{AB}.\overrightarrow{BC} +
\overrightarrow{AB}.\overrightarrow{CA} = 0\)
Ví dụ 2: Cho tam giác nhọn\(ABC\), \(AH\) là đường cao. Chứng minh rằng:
a) \(\overrightarrow{AB}.\overrightarrow{AH} =
\overrightarrow{AC}.\overrightarrow{AH}\) b) \(\overrightarrow{AB}.\overrightarrow{BC} =
\overrightarrow{HB}.\overrightarrow{BC}\)
Hướng dẫn giải
Hình vẽ minh họa:
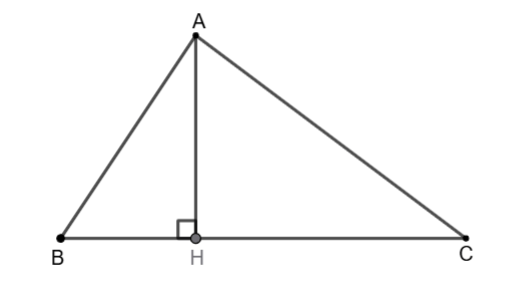
a) Ta có
\(\overrightarrow{AB}.\overrightarrow{AH} =
\overrightarrow{AC}.\overrightarrow{AH}(1) \Leftrightarrow
\overrightarrow{AB}.\overrightarrow{AH} -
\overrightarrow{AC}.\overrightarrow{AH} = 0\)
\(\Leftrightarrow
\overrightarrow{AH}(\overrightarrow{AB} - \overrightarrow{AC}) = 0
\Leftrightarrow \overrightarrow{AH}.\overrightarrow{CB} =
0(2)\)
Vì \(\overrightarrow{AH}\bot\overrightarrow{CB}\) nên \(\overrightarrow{AH}.\overrightarrow{CB}
= 0\). Do đó (2) luôn đúng nên (1) đúng.
Vạy \(\overrightarrow{AB}.\overrightarrow{AH} =
\overrightarrow{AC}.\overrightarrow{AH}\)
b) Ta có: \(\overrightarrow{AB}.\overrightarrow{BC} =
\overrightarrow{HB}.\overrightarrow{BC} \Leftrightarrow
\overrightarrow{BC}(\overrightarrow{AB} - \overrightarrow{HB}) = 0
\Leftrightarrow \overrightarrow{BC}.\overrightarrow{AH} =
0.\)
Vậy \(\overrightarrow{AB}.\overrightarrow{BC} =
\overrightarrow{HB}.\overrightarrow{BC}\)
Ví dụ 3: Cho \(I\) là trung điểm của đoạn thẳng \(AB\) và \(M\) là điểm tùy ý.
Chứng minh rằng : \(\overrightarrow{MA}.\overrightarrow{MB} = IM^{2} -
IA^{2}\).
Hướng dẫn giải
Đẳng thức cần chứng minh được viết lại là \(\overrightarrow{MA}.\overrightarrow{MB} =
{\overrightarrow{IM}}^{2} - {\overrightarrow{IA}}^{2}\)
Để làm xuất hiện \(\overrightarrow{IM},\ \
\overrightarrow{IA}\) ở vế phải, sử dụng quy tắc ba điểm để xen điểm \(I\) vào ta được
\(VT = \left( \overrightarrow{MI} +
\overrightarrow{IA} \right).\left( \overrightarrow{MI} +
\overrightarrow{IB} \right) = \left( \overrightarrow{MI} +
\overrightarrow{IA} \right).\left( \overrightarrow{MI} -
\overrightarrow{IA} \right)\)
\(= {\overrightarrow{IM}}^{2} -
{\overrightarrow{IA}}^{2} = VP\) (điều phải chứng minh).
Ví dụ 4: Chứng minh rằng với mọi tam giác ABC, ta có:
\(S_{ABC} =
\frac{1}{2}\sqrt{{\overrightarrow{AB}}^{2}.{\overrightarrow{AC}}^{2} -
\left( \overrightarrow{AB}.\overrightarrow{AC} \right)^{2}}\)
Hướng dẫn giải
Ta có \(S = \frac{1}{2}AB.AC.sinA
\Rightarrow S^{2} = \frac{1}{4}AB^{2}.AC^{2}\left( 1 - cos^{2}A
\right)\)
Hay \(S^{2} =
\frac{1}{4}AB^{2}.AC^{2}\left\lbrack 1 - \frac{\left(
\overrightarrow{AB}.\overrightarrow{AC} \right)^{2}}{AB^{2}.AC^{2}}
\right\rbrack = \frac{1}{4}\left\lbrack AB^{2}.AC^{2} - \left(
\overrightarrow{AB}.\overrightarrow{AC} \right)
\right\rbrack\)
Vậy \(S_{ABC} =
\frac{1}{2}\sqrt{{\overline{AB}}^{2} \cdot {\overline{AC}}^{2} - \left(
\overline{AB} \cdot \overline{AC} \right)^{2}}\).
C. Bài tập tự rèn luyện có đáp án chi tiết
Bài tập 1: Cho tam giác ABC có trọng tâm G. Chứng minh rằng với mọi điểm M, ta có: \(MA^{2} + MB^{2} + MC^{2} =
3MG^{2} + GA^{2} + GB^{2} + GC^{2}\).
Bài tập 2: Cho bốn điểm \(A,B,C,D\) bất kì. Chứng minh rằng: \(\overrightarrow{DA}.\overrightarrow{BC} +
\overrightarrow{DB}.\overrightarrow{CA} +
\overrightarrow{DC}.\overrightarrow{AB} = 0\)(*).
Từ đó suy ra một cách chứng minh định lí: "Ba đường cao trong tam giác đồng quy".
Bài tập 3: Cho nửa đường tròn đường kính \(AB\). Có \(AC\) và \(BD\) là hai dây thuộc nửa đường tròn cắt nhau tại \(E\). Chứng minh rằng: \(\overrightarrow{AE}.\overrightarrow{AC} +
\overrightarrow{BE}.\overrightarrow{BD} = AB^{2}\).
Bài tập 4: Cho tam giác \(ABC\)có \(BC = a,\ CA = b,\ AB = c\) và \(I\) là tâm đường tròn nội tiếp. Chứng minh rằng \(aIA^{2} + bIB^{2} + cIC^{2} =
abc\).
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu
---------------------------------------------------
Qua bài viết Chứng minh đẳng thức vectơ về tích vô hướng Toán 10, bạn đã nắm được phương pháp chứng minh, công thức cơ bản và cách vận dụng tích vô hướng trong các bài toán vectơ. Việc luyện tập thường xuyên với các bài tập tích vô hướng lớp 10 sẽ giúp bạn tư duy linh hoạt, giải nhanh đề thi và tự tin chinh phục mọi dạng bài trong chương trình Toán 10.
