Công thức tính các số đặc trưng trong Thống kê mẫu số liệu không ghép nhóm
Công thức tính trong mẫu số liệu không ghép nhóm
Trong thống kê, việc xác định các số đặc trưng của mẫu số liệu không ghép nhóm đóng vai trò quan trọng để mô tả và phân tích dữ liệu. Những đại lượng như số trung bình cộng, mốt, trung vị, tứ phân vị… giúp người học nắm bắt xu hướng tập trung, mức độ phân tán và đặc điểm nổi bật của dữ liệu. Ở chương trình Toán 10 – Chuyên đề Công thức mẫu số liệu không ghép nhóm, học sinh sẽ được hệ thống đầy đủ các công thức cần thiết để giải nhanh và chính xác các dạng bài tập thống kê. Bài viết này sẽ giới thiệu chi tiết công thức tính các số đặc trưng trong mẫu số liệu không ghép nhóm, kèm theo hướng dẫn áp dụng và ví dụ minh họa cụ thể.
1. Số trung bình cộng
Kí hiệu: ![]() \(\overline{x}\)
\(\overline{x}\)
Mẫu số liệu ![]() \(x_{1},\ x_{2}\ ,\ ...,\
x_{n}\) thì
\(x_{1},\ x_{2}\ ,\ ...,\
x_{n}\) thì ![]() \(\overline{x} =
\frac{x_{1} + x_{2} + ... + x_{n}}{n}\)
\(\overline{x} =
\frac{x_{1} + x_{2} + ... + x_{n}}{n}\)
Mẫu số liệu cho dưới dạng bảng phân bố tần số - Tần suất
|
Tên dữ liệu |
Tần số |
Tần suất (%) |
|
x1 x2 . xk |
n1 n2 . nk |
f1 f2 . fk |
|
Cộng |
n=n1+…+nk |
100 % |
Trung bình cộng của các số liệu thống kê được tính theo công thức:
![]() \(\boxed{\overline{x} =
\frac{1}{n}(n_{1}x_{1} + n_{2}x_{2} + ... + n_{k}x_{k}) = f_{1}x_{1} +
f_{2}x_{2} + ... + f_{k}x_{k}}\ \ \ (1)\)
\(\boxed{\overline{x} =
\frac{1}{n}(n_{1}x_{1} + n_{2}x_{2} + ... + n_{k}x_{k}) = f_{1}x_{1} +
f_{2}x_{2} + ... + f_{k}x_{k}}\ \ \ (1)\)
Ý nghĩa của số trung bình:
Số trung bình của mẫu số liệu được dùng làm đại diện cho các số liệu của mẫu. Nó là một số đặc trưng quan trọng của mẫu số liệu.
2. Số trung vị
Kí hiệu: ![]() \(M_{e}\)
\(M_{e}\)
Khi các số liệu trong mẫu có sự chênh lệnh rất lớn đối với nhau thì số trung bình khó có thể đại diện cho các số liệu trong mẫu. Có một chỉ số khác thích hợp hơn trong trường hợp này. Đó là số trung vị.
Định nghĩa: Giả sử ta có dãy n số liệu được sắp xếp thành dãy không giảm (hoặc không tăng). Khi đó, số trung vị (của các số liệu thống kê đã cho) kí hiệu là ![]() \(M_{e}\) là:
\(M_{e}\) là:
+ Số đứng giữa dãy nếu số phần tử N lẻ: ![]() \(M_{e} = x_{\frac{N}{2} + 1}\)
\(M_{e} = x_{\frac{N}{2} + 1}\)
+ Trung bình cộng của hai số đứng giữa dãy nếu số phần tử N chẵn: ![]() \(M_{e} = \frac{1}{2}(x_{\frac{N}{2}} +
x_{\frac{N}{2} + 1})\)
\(M_{e} = \frac{1}{2}(x_{\frac{N}{2}} +
x_{\frac{N}{2} + 1})\)
3. Tứ phân vị
Sắp thứ tự mẫu số liệu gồm n số liệu thành một dãy không giảm
- Tìm số trung vị: giá trị này là
 \(Q_{2}\)
\(Q_{2}\) - Tìm trung vị của nữa số liệu bên trái
 \(Q_{2}\)(không gồm
\(Q_{2}\)(không gồm  \(Q_{2}\) nếu n lẻ): giá trị này là
\(Q_{2}\) nếu n lẻ): giá trị này là  \(Q_{1}\)
\(Q_{1}\) - Tìm trung vị của nữa số liệu bên phảii
 \(Q_{2}\)(không gồm
\(Q_{2}\)(không gồm  \(Q_{2}\) nếu n lẻ): giá trị này là
\(Q_{2}\) nếu n lẻ): giá trị này là  \(Q_{3}\)
\(Q_{3}\) - Tứ phân vị của mẫu số liệu là bộ ba giá trị
 \(Q_{1},\ Q_{2},\ Q_{3}.\)
\(Q_{1},\ Q_{2},\ Q_{3}.\)
Chú ý:
 \(Q_{1}\) gọi là tứ phân vị thứ nhất hay tứ phân vị dưới.
\(Q_{1}\) gọi là tứ phân vị thứ nhất hay tứ phân vị dưới. \(Q_{2}\): gọi là tứ phân vị thứ hai (
\(Q_{2}\): gọi là tứ phân vị thứ hai ( \(Q_{2}\) bằng số trung vị)
\(Q_{2}\) bằng số trung vị) \(Q_{3}\) gọi là tứ phân vị thứ bat hay tứ phân vị trên.
\(Q_{3}\) gọi là tứ phân vị thứ bat hay tứ phân vị trên.
Ý nghĩa:
Các điểm ![]() \(Q_{1},\ Q_{2},\
Q_{3}.\)chia mẫu số liệu đã sắp xếp theo thứ tự từ nhỏ đến lớn thành bốn phần có số lượng phần tử bằng nhau. Mỗi phần chứa
\(Q_{1},\ Q_{2},\
Q_{3}.\)chia mẫu số liệu đã sắp xếp theo thứ tự từ nhỏ đến lớn thành bốn phần có số lượng phần tử bằng nhau. Mỗi phần chứa ![]() \(25\%\) giá trị.
\(25\%\) giá trị.
Bộ ba giá trị ![]() \(Q_{1},\ Q_{2},\
Q_{3}.\)trong tứ phân vị phản ánh độ phân tán của mẫu số liệu. Những mỗi giá trị
\(Q_{1},\ Q_{2},\
Q_{3}.\)trong tứ phân vị phản ánh độ phân tán của mẫu số liệu. Những mỗi giá trị ![]() \(Q_{1},\ Q_{2},\
Q_{3}.\)lại đo xu thế trung tâm của phần số liệu tương ứng của mẫu đó.
\(Q_{1},\ Q_{2},\
Q_{3}.\)lại đo xu thế trung tâm của phần số liệu tương ứng của mẫu đó.
Cách tìm tứ phân vị:
Để tìm các tứ phân vị của mẫu số liệu có ![]() \(n\) giá trị, ta làm như sau:
\(n\) giá trị, ta làm như sau:
- Sắp xếp mẫu số liệu theo thứ tự không giảm.
- Tìm trung vị. Giá trị này là
 \(Q_{2}\).
\(Q_{2}\). - Tìm trung vị của nửa số liệu bên trái
 \(Q_{2}\) (không bao gồm
\(Q_{2}\) (không bao gồm  \(Q_{2}\) nếu
\(Q_{2}\) nếu  \(n\) lẻ). Giá trị này là
\(n\) lẻ). Giá trị này là  \(Q_{1}\).
\(Q_{1}\). - Tìm trung vị của nửa số liệu bên phải
 \(Q_{2}\) (không bao gồm
\(Q_{2}\) (không bao gồm  \(Q_{2}\) nếu
\(Q_{2}\) nếu  \(n\) lẻ). Giá trị này là
\(n\) lẻ). Giá trị này là  \(Q_{3}\).
\(Q_{3}\).  \(Q_{1},\ \ Q_{2},\ \ Q_{3}\) được gọi là các tứ phân vị của mẫu số liệu
\(Q_{1},\ \ Q_{2},\ \ Q_{3}\) được gọi là các tứ phân vị của mẫu số liệu
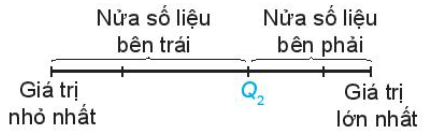
Chú ý. ![]() \(Q_{1}\) được gọi là tứ phân vị thứ nhất hay tứ phân vị dưới,
\(Q_{1}\) được gọi là tứ phân vị thứ nhất hay tứ phân vị dưới, ![]() \(Q_{3}\) được gọi là tứ phân vị thứ ba hay tứ phân vị trên.
\(Q_{3}\) được gọi là tứ phân vị thứ ba hay tứ phân vị trên.
Ý nghĩa. Các điểm ![]() \(Q_{1},\ Q_{2},\
Q_{3}\) chia mẫu số liệu đã sắp xếp theo thứ tự từ nhỏ đến lớn thành bốn phần, mỗi phần đều chứa
\(Q_{1},\ Q_{2},\
Q_{3}\) chia mẫu số liệu đã sắp xếp theo thứ tự từ nhỏ đến lớn thành bốn phần, mỗi phần đều chứa ![]() \(25\%\) giá trị (hình vẽ).
\(25\%\) giá trị (hình vẽ).

4. Mốt
Kí hiệu: ![]() \(M_{0}\)
\(M_{0}\)
Mốt của bảng phân bố tần số là giá trị (xi) có tần số (ni ) lớn nhất và được kí hiệu là ![]() \(M_{0}\).
\(M_{0}\).
Chú ý: Có hai giá trị tần số bằng nhau và lớn hơn tần số các giá trị khác thì ta nói trường hợp này có hai Mốt, kí hiệu ![]() \(M_{0}^{(1)},M_{0}^{(2)}\) .
\(M_{0}^{(1)},M_{0}^{(2)}\) .
5. Tính hợp lí của số liệu thống kê
Sau khi thu thập, tổ chức, phân loại và biểu diễn số bằng bảng hoặc biếu đồ, ta cần phân tích và xử lí các số liệu đó để xem xét tính hợp lí của số liệu thống kê, đặc biệt chỉ ra được những số liệu bất thường (hay còn gọi là dị biệt). Ta có thể sử dụng các số liệu đắc trưng đo xu thế trung tâm cho mẫu số liệu không ghép nhóm để thực hiện diều đó.
6. Chọn đại diện cho các số liệu thống kê
a) Trường hợp các số liệu thông kê cùng loại và số lượng thống kê đủ lớn (n ≥ 30) thì ta ưu tiên chọn số trung bình làm đại diện cho các số liệu thống kê (về quy mô và độ lớn).
b) Trường hợp không tính được giá trị trung bình thì ta chọn số trung vị hoặc mốt làm đại diện cho các số liệu thống kê (về quy mô và độ lớn).
c) Không nên dùng số trung bình để đại diện cho các số liệu thống kê trong các trường hợp sau (có thể dùng số trung vị hoặc mốt):
+ Số các số liệu thống kê quá ít (n ≤ 10).
+ Giữa các số liệu thống kê có sự chênh lệc quá lớn.
+ Đường gấp khúc tần suất không đối xứng, (và nhiều trường hợp khác)
7. Khoảng biến thiên và khoảng tứ phân vị
Khoảng biến thiên, kí hiệu là R, là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất trong mẫu số liệu.
Ý nghĩa. Khoảng biến thiên dùng để đo độ phân tán của mẫu số liệu. Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán.
Nhận xét. Sử dụng khoảng biến thiên có ưu điểm là đơn giản, dễ tính toán song khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và giá trị nhỏ nhất mà bỏ qua thông tin từ tất cả các giá trị khác. Do đó, khoảng biến thiên rất dễ bị ảnh hưởng bởi các giá trị bất thường.
Khoảng tứ phân vị, kí hiệu ![]() \(\Delta_{Q}\), là hiệu số giữa tứ phân vị thứ ba và tứ phân vị thứ nhất, túc là:
\(\Delta_{Q}\), là hiệu số giữa tứ phân vị thứ ba và tứ phân vị thứ nhất, túc là:
![]() \(\Delta_{Q} = Q_{3} - Q_{1}\)
\(\Delta_{Q} = Q_{3} - Q_{1}\)
Ý nghĩa. Khoảng tứ phân vị cũng là một số đo độ phân tán của mẫu số liệu. Khoảng tứ phân vị càng lớn thì mẫu số liệu càng phân tán.
Chú ý. Một số tài liệu gọi khoảng biến thiên là biên độ và khoảng tứ phân vị là độ trải giữa.
8. Phương sai và độ lệch chuẩn
Khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và nhỏ nhất của mẫu số liệu (bỏ qua thông tin của tất cả các giá trị khác), còn khoảng tứ phân vị chỉ sử dụng thông tin của 50% số liệu chính giữa. Có một vài số đặc trưng khác đo độ phân tán sử dụng thông tin của tất cả các giá trị trong mẫu số liệu. Hai trong số đó là phương sai và độ lệch chuẩn.
Cụ thể là với mẫu số liệu ![]() \(x_{1},\
x_{2},...,\ x_{n}\), nếu gọi số trung bình là
\(x_{1},\
x_{2},...,\ x_{n}\), nếu gọi số trung bình là ![]() \(\overline{x}\) thì với mỗi giá trị
\(\overline{x}\) thì với mỗi giá trị ![]() \(x_{i}\), độ lệch của nó so với giá trị trung bình là
\(x_{i}\), độ lệch của nó so với giá trị trung bình là ![]() \(x_{i} -
\overline{x}\).
\(x_{i} -
\overline{x}\).
a) Phương sai: Kí hiệu ![]() \(s_{x}^{2}\)
\(s_{x}^{2}\)
Trường hợp bảng phân bố tần số, tần suất
![]() \(s_{x}^{2} = \frac{1}{n}\left\lbrack
n_{1}(x_{1} - \overline{x})^{2} + n_{2}(x_{2} - \overline{x})^{2} + ...
+ n_{k}(x_{k} - \overline{x})^{2} \right\rbrack\)
\(s_{x}^{2} = \frac{1}{n}\left\lbrack
n_{1}(x_{1} - \overline{x})^{2} + n_{2}(x_{2} - \overline{x})^{2} + ...
+ n_{k}(x_{k} - \overline{x})^{2} \right\rbrack\)
![]() \(= f_{1}(x_{1} - \overline{x})^{2} +
f_{2}(x_{2} - \overline{x})^{2} + ... + f_{k}(x_{k} -
\overline{x})^{2}.\)
\(= f_{1}(x_{1} - \overline{x})^{2} +
f_{2}(x_{2} - \overline{x})^{2} + ... + f_{k}(x_{k} -
\overline{x})^{2}.\)
Ý nghĩa phương sai
Phương sai được sử dụng để đánh giá mức độ phân tán của các số liệu thống kê (so với số trung bình).
Khi hai dãy số liệu thống kê có cùng đơn vị đo và có số trung bình bằng nhau hoặc xấp xỉ nhau, dãy có phương sai càng nhỏ thì mức độ phân tán (so với số trung bình) của các số liệu thống kê càng bé.
b) Độ lệch chuẩn
Khi chú ý đơn vị đo ta thấy phương sai ![]() \(s_{x}^{2}\) có đơn vị đo là bình phương của đơn vị đo được nghiên cứu ( đơn vị đo nghiên cứu là
\(s_{x}^{2}\) có đơn vị đo là bình phương của đơn vị đo được nghiên cứu ( đơn vị đo nghiên cứu là ![]() \(cm\) thì
\(cm\) thì ![]() \(s_{x}^{2}\) là
\(s_{x}^{2}\) là ![]() \(cm^{2}\)), để tránh tình trạng này ta dùng căn bậc hai của phương sai gọi là độ lệch chuẩn.
\(cm^{2}\)), để tránh tình trạng này ta dùng căn bậc hai của phương sai gọi là độ lệch chuẩn.
Độ lệch chuẩn, kí hiệu là ![]() \(s_{x}\)
\(s_{x}\)
![]() \(s_{x} = \sqrt{s_{x}^{2}}\)
\(s_{x} = \sqrt{s_{x}^{2}}\)
Ý nghĩa độ lệch chuẩn: Độ lệch chuẩn cũng dùng đánh giá mức độ phân tán của các số liệu thống kê (so với số trung bình). Khi cần chú ý đến đơn vị đo ta dùng độ lệch chuẩn để đánh giá vì độ lệch chuẩn có cùng đơn vị đó với dấu hiệu X được nghiên cứu.
Chú ý. Người ta còn sử dụng đại lượng để đo độ phân tán của mẫu số liệu:
![]() \({\widehat{s}}^{2} = \frac{\left( x_{1} -
\overline{x} \right)^{2} + \left( x_{2} - \overline{x} \right)^{2} + ...
+ \left( x_{n} - \overline{x} \right)^{2}}{n - 1}\).
\({\widehat{s}}^{2} = \frac{\left( x_{1} -
\overline{x} \right)^{2} + \left( x_{2} - \overline{x} \right)^{2} + ...
+ \left( x_{n} - \overline{x} \right)^{2}}{n - 1}\).
Ý nghĩa. Nếu số liệu càng phân tán thì phương sai và độ lệch chuẩn càng lớn.
------------------------------------------------------------
Qua bài viết, bạn đã được trang bị kiến thức trọng tâm về công thức tính các số đặc trưng trong thống kê mẫu số liệu không ghép nhóm, bao gồm trung bình cộng, mốt, trung vị và tứ phân vị. Đây là nền tảng quan trọng của Toán 10, thường xuyên xuất hiện trong đề kiểm tra và kỳ thi. Việc nắm chắc các công thức này sẽ giúp bạn xử lý số liệu nhanh chóng, chính xác và phát triển kỹ năng phân tích dữ liệu khoa học. Hãy luyện tập thêm nhiều dạng bài tập để củng cố kiến thức và tự tin đạt điểm cao trong môn Toán.









