Độ dài Vectơ Toán 10 – Hướng dẫn giải và bài tập Có lời giải
Cách tính độ dài vectơ Toán 10 chi tiết
Trong chương trình Toán 10, việc tìm hiểu về độ dài vectơ là bước quan trọng giúp học sinh hiểu rõ mối liên hệ giữa đại số và hình học. Nắm vững công thức tính độ dài vectơ, quy tắc xác định và cách áp dụng vào bài tập thực tế sẽ giúp bạn học tốt hơn các chuyên đề tiếp theo như tọa độ vectơ, phương trình đường thẳng và tích vô hướng.
Bài viết này sẽ hướng dẫn bạn cách tính độ dài vectơ Toán 10 chi tiết, kèm bài tập minh họa có lời giải, giúp bạn dễ hiểu – dễ nhớ – dễ áp dụng trong quá trình ôn luyện và làm bài kiểm tra.
A. Độ dài vectơ
Độ dài đoạn thẳng 
\(AB\) gọi là độ dài vectơ \(\overrightarrow{AB}\), kí hiệu \(\left| \overrightarrow{AB}
\right|\).
B. Ví dụ minh họa tính độ dài vectơ
Ví dụ 1: Cho \(\Delta ABC\) vuông tại \(A\) và \(AB = 5,BC = 8.\)
a. Tìm độ dài của vectơ \(\overrightarrow{AC}\).
b. Gọi \(M\) là trung điểm \(BC\). Tìm \(\left| \overrightarrow{AM} \right|\) ?
c. Gọi \(H\) là hình chiếu cỉa \(A\) trên \(BC\). Tìm \(\left| \overrightarrow{AH} \right|\)?
d. Gọi G là trọng tâm của \(\Delta
ABC\). Tìm độ dài \(\overrightarrow{AG}\).
Hướng dẫn giải
Hình vẽ minh họa:
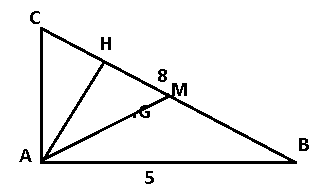
a. Áp dụng định lí Pythagore cho tam giác ABC vuông tại A ta được:
\(\left| \overrightarrow{AC} \right| = AC
= \sqrt{BC^{2} - AB^{2}} = \sqrt{8^{2} - 5^{2}} =
\sqrt{39}.\)
b. Ta có \(\left| \overrightarrow{AM}
\right| = AM = \frac{BC}{2} = 4.\)
c. Ta có \(\frac{1}{AH^{2}} =
\frac{1}{AB^{2}} + \frac{1}{AC^{2}} = \frac{1}{5^{2}} +
\frac{1}{(\sqrt{39})^{2}} = \frac{64}{975}\)
\(\Rightarrow AH =
\frac{5\sqrt{39}}{8}.\)
Vậy \(\left| \overrightarrow{AH} \right| =
AH = \frac{5\sqrt{39}}{8}.\)
d) \(\left| \overrightarrow{AG} \right| =
\frac{2}{3}AM = \frac{2}{3}4 = \frac{8}{3}.\)
Ví dụ 2: Cho tam giác ABC vuông cân tại A, có \(AB = AC = 5\). Tính \(\left| \overrightarrow{BC} \right|\)?
Hướng dẫn giải
Hình vẽ minh họa:
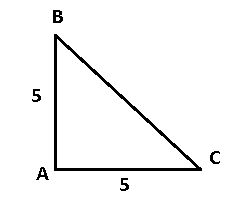
Ta có: \(\left| \overrightarrow{BC} \right|
= BC = \sqrt{AB^{2} + AC^{2}} = \sqrt{5^{2} + 5^{2}} =
5\sqrt{2}.\)
Ví dụ 3: Cho \(\Delta ABC\) đều có cạnh bằng \(a\).
a) Tìm theo \(a\) độ dài của vectơ \(\overrightarrow{AB}\).
b) Gọi \(H\) là trung điểm \(BC\). Tìm \(\left| \overrightarrow{AH} \right|\) ?
c. Gọi G là trọng tâm của \(\Delta
ABC\). Tìm độ dài của \(\overrightarrow{BG}\)?
Hướng dẫn giải
Hình vẽ minh họa:
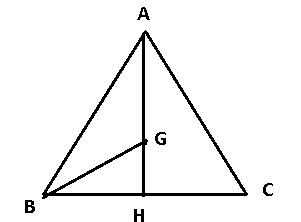
a. Ta có: \(\left| \overrightarrow{AB}
\right| = AB = a.\)
b. Áp dụng định lí Pi-ta-go trong tam giác vuông \(AHC\) ta được:
\(AH = \sqrt{AC^{2} - HC^{2}} =
\sqrt{a^{2} - (\frac{a}{2})^{2}} = \frac{a\sqrt{3}}{2}.\)
\(\left| \overrightarrow{AH} \right| = AH
= \frac{a\sqrt{3}}{2}.\)
c. Vì G là trọng tâm của \(\Delta
ABC\) nên \(GH = \frac{1}{3}AH =
\frac{1}{3}.\frac{a\sqrt{3}}{2} = \frac{a\sqrt{3}}{6}.\)
\(BG = \sqrt{GH^{2} + HB^{2}} =
\sqrt{\left( \frac{a\sqrt{3}}{6} \right)^{2} + \left( \frac{a}{2}
\right)^{2}} = \frac{a\sqrt{3}}{3}.\)
Vậy \(\left| \overrightarrow{BG} \right| =
BG = \frac{a\sqrt{3}}{3}.\)
Ví dụ 4: Cho tam giác \(ABC\) có \(AB = 2\ cm\), \(AC = 1\ cm\), \(\widehat{A} = 60{^\circ}\). Tính \(\left| \overrightarrow{BC} \right|\)?
Hướng dẫn giải
Ta có \(BC^{2} = AB^{2} + AC^{2} -
2AB.AC.cosA\)
\(\Rightarrow BC^{2} = 2^{2} + 1^{2} -
2.2.1.cos60{^\circ} \Rightarrow BC^{2} = 3 \Rightarrow BC =
\sqrt{3}.\)
Vậy \(\left| \overrightarrow{BC} \right| =
BC = \sqrt{3}\ .\)
C. Bài tập tự rèn luyện tính độ dài vectơ có đáp án chi tiết
Bài tập 1: Cho hình vuông \(ABCD\) có tâm \(O\) , có độ dài cạnh \(7\).
a. Tìm \(|\
\overrightarrow{AC}|\)?
b. Tìm độ dài của vectơ \(\overrightarrow{OA}\)
Bài tập 2. Cho hình chữ nhật \(ABCD\) có \(\widehat{BAC} = 60^{0}\) và \(AC = 3a\), tìm độ dài của vectơ \(\overrightarrow{BC}\) .
Bài tập 3: Cho hình thoi \(ABCD\) cạnh \(a\) và \(\widehat{BAD} = 60{^\circ}\). Tìm độ dài của vectơ \(\overrightarrow{AC}\)?
Bài tập 4: Trên mặt phẳng tọa độ Oxy, hãy vẽ các vecto \(\overrightarrow{OA},\
\overrightarrow{MN}\) với A(1; 2), M(0; -1), N(3; 5).
a. Chỉ ra mối quan hệ giữa hai vecto trên.
b. Một vật thể khởi hành từ M và chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu diễn bởi vectơ \(\overrightarrow{v} = \overrightarrow{OA}\). Hỏi vật thể đó có đi qua N hay không? Nếu có thì sau bao lâu vật sẽ tới N?
Bạn muốn xem toàn bộ tài liệu? Hãy nhấn Tải về ngay!
--------------------------------------------------------
Kiến thức về độ dài vectơ Toán 10 là nền tảng quan trọng trong hình học giải tích và các bài toán tọa độ ở bậc THPT. Hy vọng với hướng dẫn chi tiết, ví dụ minh họa và bài tập có lời giải trong bài viết, bạn đã hiểu rõ bản chất, nắm vững công thức tính và biết cách vận dụng linh hoạt vào từng dạng bài.
