Khoảng tứ phân vị là gì? Cách tính trong mẫu số liệu không ghép nhóm
Cách tính khoảng tứ phân vị trong mẫu số liệu không ghép nhóm
Trong thống kê, ngoài việc tìm các số đặc trưng như trung bình, mốt, trung vị, tứ phân vị, thì khoảng tứ phân vị (Interquartile Range – IQR) cũng là một đại lượng quan trọng. Đây là chỉ số phản ánh mức độ phân tán của dữ liệu, giúp nhận biết sự chênh lệch giữa nhóm số liệu cao và thấp. Ở mẫu số liệu không ghép nhóm Toán 10, việc tính khoảng tứ phân vị giúp học sinh hiểu rõ hơn về sự biến động của dữ liệu và ứng dụng vào giải toán thống kê. Bài viết này sẽ giải thích chi tiết khoảng tứ phân vị là gì, công thức và cách tính trong mẫu số liệu không ghép nhóm, kèm theo bài tập minh họa có đáp án để bạn dễ dàng nắm vững kiến thức.
A. Khoảng tứ phân vị là gì?
Khoảng tứ phân vị, kí hiệu 
\(\Delta_{Q}\), là hiệu số giữa tứ phân vị thứ ba và tứ phân vị thứ nhất, túc là:
\(\Delta_{Q} = Q_{3} - Q_{1}\)
Ý nghĩa. Khoảng tứ phân vị cũng là một số đo độ phân tán của mẫu số liệu. Khoảng tứ phân vị càng lớn thì mẫu số liệu càng phân tán.
Chú ý. Một số tài liệu gọi khoảng biến thiên là biên độ và khoảng tứ phân vị là độ trải giữa.
B. Bài tập minh họa tìm khoảng tứ phân vị của mẫu số liệu không ghép nhóm
Ví dụ. Mẫu số liệu sau cho biết số ghế trống tại một rạp chiếu phim trong 9 ngày:
7 8 22 20 15 18 19 13 11.
Tìm khoảng tứ phân vị cho mẫu số liệu này.
Hướng dẫn giải
Trước hết, ta sắp xếp mẫu số liệu theo thứ tự không giảm:
7 8 11 13 15 18 19 20 22.
Mẫu số liệu gồm 9 giá trị nên trung vị là số ở vị trí chính giữa \(Q_{2} = 15\).
Nửa số liệu bên trái là 7, 8, 11, 13 gồm 4 giá trị, hai phần tử chính giữa là 8, 11.
Do đó, \(Q_{1} = (8 + 11):2 =
9,5\).
Nửa số liệu bên phải là 18, 19, 20, 22 gồm 4 giá trị, hai phần tử chính giữa là 19, 20.
Do đó, \(Q_{3} = (19 + 20):2 =
19,5\).
Vậy khoảng tứ phân vị cho mẫu số liệu là: \(\Delta_{Q} = 19,5 - 9,5 = 10\).
Ví dụ: Hãy khoảng tứ phân vị của các mẫu số liệu sau:
a) \(10;\ 13;\ 15;\ 2;\ 10;\ 19;\ 2;\ 5;\
7.\)
b) \(15;\ 19;\ 10;\ 5;\ 9;\ 10;\ 1;\ 2;\
5;\ 15.\)
Hướng dẫn giải
a) Sắp xếp mẫu số liệu theo thứ tự không giảm, ta được:
\(2;\ 2;\ 5;\ 7;\ 10;\ 10;\ 13;\ 15;\
19.\)
Cỡ mẫu là \(n = 9\) là số lẻ nên giá trị tứ phân vị thứ hai là: \(Q_{2} =
10\)
Tứ phân vị thứ nhất là trung vị của mẫu: \(2;\ 2;\ 5;\ 7\).
Do đó \(Q_{1} = \frac{2 + 5}{2} =
3,5\)
Tứ phân vị thứ ba là trung vị của mẫu: \(\
10;\ 13;\ 15;\ 19.\)
Do đó \(Q_{3} = \frac{13 + 15}{2} =
14\)
Khoảng tứ phân vị của mẫu là: \(\Delta Q =
Q_{3} - Q_{1} = 14 - 3,5 = 10,5\).
b) Sắp xếp mẫu số liệu theo thứ tự không giảm, ta được:
\(1;\ 2;\ 5;\ 5;\ 9;\ 10;\ 10;\ 15;\ 15;\
19.\)
Cỡ mẫu là \(n = 10\) là số chẵn nên giá trị tứ phân vị thứ hai là: \(Q_{2} =
\frac{9 + 10}{2} = 9,5\)
Tứ phân vị thứ nhất là trung vị của mẫu: \(1;\ 2;\ 5;\ 5;\ 9.\)
Do đó \(Q_{1} = 5\)
Tứ phân vị thứ ba là trung vị của mẫu: \(10;\ 10;\ 15;\ 15;\ 19.\)
Do đó \(Q_{3} = 15\)
Khoảng tứ phân vị của mẫu là: \(\Delta Q =
Q_{3} - Q_{1} = 15 - 5 = 10\).
Ví dụ: Mẫu số liệu sau đây cho biết cân nặng của 10 trẻ sơ sinh (đơn vị kg):
\(\begin{matrix}
2,977\ \ \ \ \ \ 3,155\ \ \ \ \ \ \ 3,920\ \ \ \ \ \ 3,412\ \ \ \ \ \
4,236 \\
2,593\ \ \ \ \ \ 3,270\ \ \ \ \ \ 3,813\ \ \ \ \ \ \ \ 4,042\ \ \ \ \
3,387
\end{matrix}\)
Hãy tính khoảng tứ phân vị cho mẫu số liệu này.
Hướng dẫn giải
Trước hết, ta sẽ sắp xếp mẫu số liệu theo thứ tự không giảm:
\(2,593\ \ \ \ \ \ \ \ \ \ \ \ 2,977\ \ \
\ \ \ \ 3,155\ \ \ \ \ \ \ \ \ \ \ 3,270\ \ \ \ \ \ \ \ \ 3,387\ \ \ \ \
\ \ \ \\)
\(3,412\ \ \ \ \ \ \ \ \ \ \ \ 3,813\ \ \
\ \ \ 3,920\ \ \ \ \ \ \ 4,042\ \ \ \ \ \ \ \ \ \ 4,236\)
Ta có: \(Q_{2} = 3,3995\); \(Q_{1} = 3,155\); \(Q_{3} = 3,920\)
C. Bài tập tự rèn luyện có hướng dẫn chi tiết
Bài tập 1: Từ mẫu số liệu về thuế thuốc lá của \(55\) thành phố tại một quốc gia, người Khoảng tứ phân vị là \(\Delta_{Q} = Q_{3} -
Q_{1} = 0,765\). ta tính được:
Giá trị nhỏ nhất bằng \(2,3\), \(Q_{1} = 38,\ \ Q_{2} = 70,\ Q_{3} = 100\) ; giá trị lớn nhất bằng \(205\). (Giả sử không có số liệu nào có giá trị bằng nhau)
a) Tỉ lệ thành phố có thuế thuốc lá lớn hơn \(38\) là bao nhiêu?
b) Tìm khoảng tứ phân vị của mẫu số liệu.
Bài tập 2: Biểu đồ đoạn thẳng ở Hình 3 biểu diễn tốc độ tăng trưởng GDP của Việt Nam giai đoạn 2012 – 2019.
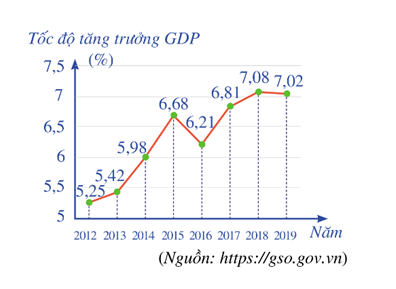
a) Viết mẫu số liệu thống kê tốc độ tăng trưởng GDP nhận được từ biểu đồ ở hình vẽ.
b) Tìm khoảng tứ phân vị của mẫu số liệu đó.
Bạn muốn xem toàn bộ tài liệu? Hãy nhấn Tải về ngay!
---------------------------------------------------------
Qua bài viết, bạn đã được tìm hiểu về khái niệm khoảng tứ phân vị, công thức áp dụng cũng như cách tính cụ thể trong mẫu số liệu không ghép nhóm Toán 10. Đây là một chỉ số quan trọng trong thống kê, giúp đánh giá mức độ phân tán và loại bỏ ảnh hưởng của những số liệu bất thường. Việc nắm chắc phương pháp tính khoảng tứ phân vị sẽ giúp bạn học tốt hơn môn Toán, đặc biệt là ở chuyên đề thống kê, đồng thời tự tin xử lý các dạng bài tập. Hãy luyện thêm nhiều bài tập tìm khoảng tứ phân vị có đáp án để củng cố và vận dụng hiệu quả kiến thức đã học.
