Quy tắc Tính tổng và hiệu của hai Vectơ
Lý thuyết tổng hiệu vectơ Toán 10
Trong chương trình Toán 10, việc nắm vững quy tắc tính tổng và hiệu của hai vectơ là kiến thức nền tảng quan trọng trong phần hình học vectơ. Kiến thức này không chỉ giúp học sinh hiểu rõ bản chất phép cộng – trừ vectơ, mà còn hỗ trợ trực tiếp cho các chuyên đề sau như tọa độ vectơ, phương trình đường thẳng và ứng dụng trong hình học phẳng.
Bài viết dưới đây sẽ cung cấp lý thuyết, công thức tính tổng và hiệu của hai vectơ, kèm hình minh họa và ví dụ giải chi tiết, giúp bạn dễ hiểu – dễ nhớ – dễ vận dụng trong bài tập và kỳ thi Toán THPT.
1. Tổng của hai vectơ
Định nghĩa: Phép cộng hai vectơ 
\(\overrightarrow{a}\) và \(\overrightarrow{b}\) là vectơ \(\overrightarrow{a} + \overrightarrow{b}\), được xác định tùy theo vị trí của hai vectơ. Có 3 trường hợp như sau:
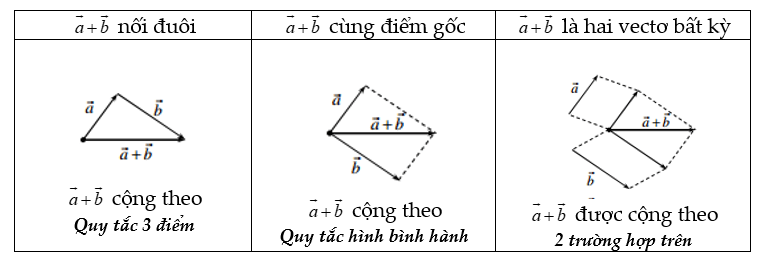
Quy tắc ba điểm
Với ba điểm bất kỳ \(A,\ B,\ C\) ta có \(\overrightarrow{AB} = \overrightarrow{AC} +
\overrightarrow{CB}\)
Quy tắc hình bình hành
Cho \(ABCD\) là hình bình hành khi đó ta có \(\left\lbrack \begin{matrix}
\overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{AD} \\
\overrightarrow{DB} = \overrightarrow{DA} + \overrightarrow{DG}
\end{matrix} \right.\)và \(\left\lbrack \begin{matrix}
\overrightarrow{AB} = \overrightarrow{DC} \\
\overrightarrow{AD} = \overrightarrow{BC}
\end{matrix} \right.\)
Tính chất
- Giao hoán: \(\overrightarrow{a} +
\overrightarrow{b} = \overrightarrow{b} +
\overrightarrow{a}\)
- Kết hợp: \(\overrightarrow{a} + \left(
\overrightarrow{b} + \overrightarrow{c} \right) = \left(
\overrightarrow{a} + \overrightarrow{c} \right) +
\overrightarrow{b}\)
- Cộng với vectơ đối: \(\overrightarrow{a}
+ \left( - \overrightarrow{a} \right) = \overrightarrow{0}\)
- Cộng với vectơ không: \(\overrightarrow{a} + \overrightarrow{0} =
\overrightarrow{0} + \overrightarrow{a} =
\overrightarrow{a}\)
2. Hiệu của hai vectơ
Vectơ đối của vectơ \(\overrightarrow{a}\) kí hiệu là \(- \overrightarrow{a}\). Đặc biệt \(\ \overrightarrow{a} + \left( - \overrightarrow{a}
\right) = \overrightarrow{0}\)
Định nghĩa: Hiệu hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) là vectơ \(\overrightarrow{a} - \overrightarrow{b} =
\overrightarrow{a} + \left( - \overrightarrow{b} \right)\)
Tính chất:
- \(\forall\overrightarrow{a}:\
\overrightarrow{a} - \overrightarrow{0} =
\overrightarrow{a}\)
- \(\forall\overrightarrow{a}:\
\overrightarrow{a} - \overrightarrow{a} =
\overrightarrow{0}\)
- \(\overrightarrow{AB} = -
\overrightarrow{BA}\)
Quy tắc tam giác đối với hiệu hai vectơ
Với ba điểm bất kì \(A,\ B,\ C\) ta có \(\overrightarrow{AB} = \overrightarrow{CB} -
\overrightarrow{CA}\)
3. Trung điểm của đoạn thẳng và trọng tâm tam giác
- Điểm I là trung điểm của đoạn \(AB
\Leftrightarrow \overrightarrow{IA} + \overrightarrow{IB} =
\overrightarrow{0}\)
- Điểm G là trọng tâm \(\Delta ABC
\Leftrightarrow \overrightarrow{GA} + \overrightarrow{GB} +
\overrightarrow{GC} = \overrightarrow{0}\)
-----------------------------------
Qua bài viết này, bạn đã được hệ thống hóa toàn bộ lý thuyết và công thức về quy tắc tính tổng và hiệu của hai vectơ Toán 10, kèm ví dụ minh họa cụ thể. Chúc bạn học tốt và đạt điểm cao trong các bài kiểm tra và kỳ thi sắp tới!
