Rút gọn biểu thức lượng giác Toán 10
Cách biến đổi và rút gọn biểu thức lượng giác Toán 10 có đáp án
Trong chương trình Toán 10, phần rút gọn biểu thức lượng giác là nội dung quan trọng giúp học sinh vận dụng thành thạo các công thức lượng giác cơ bản và biến đổi biểu thức nhanh, chính xác. Bài viết Rút gọn biểu thức lượng giác Toán 10 sẽ hướng dẫn chi tiết phương pháp rút gọn, kèm theo các bài tập minh họa, ví dụ có lời giải giúp các em hiểu sâu và nắm chắc giá trị lượng giác của một góc từ 0 đến 180 độ.
A. Cách rút gọn biểu thức lượng giác
Phương pháp giải toán:
Dùng các công thức cơ bản
\(\tan\alpha =
\frac{\sin\alpha}{\cos\alpha}(\alpha \neq 90^{0})\)- \(\cot\alpha =
\frac{\cos\alpha}{\sin\alpha}(\alpha \neq 0^{0};180^{0})\)
- \(\tan\alpha.cot\alpha = 1(\alpha \neq
0^{0};90^{0};180^{0})\)
- \(sin^{2}\alpha + cos^{2}\alpha =
1\)
- \(1 + tan^{2}\alpha =
\frac{1}{cos^{2}\alpha}(\alpha \neq 90^{0})\)
- \(1 + cot^{2}\alpha =
\frac{1}{sin^{2}\alpha}(\alpha \neq 0^{0};180^{0})\)
Dùng các công thức cung liên quan đặc biệt
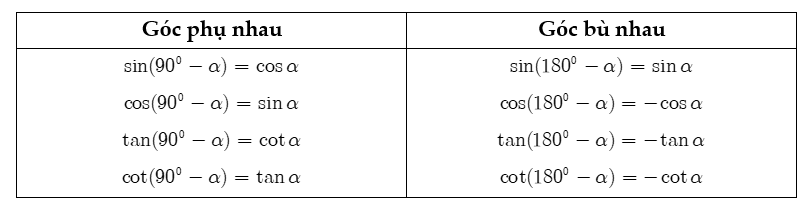
Biến đổi đại số
B. Ví dụ minh họa rút gọn biểu thức lượng giác
Ví dụ 1: Rút gọn biểu thức: \(A = (1 +
\cos\alpha)cot^{2}\alpha(1 - \cos\alpha).\)
Hướng dẫn giải
Ta có:
\(A = (1 + \cos\alpha)(1 -
\cos\alpha)cot^{2}\alpha = (1 - cos^{2}\alpha)cot^{2}\alpha\)
\(A =
sin^{2}\alpha.\frac{cos^{2}\alpha}{sin^{2}\alpha} =
cos^{2}\alpha.\)
Ví dụ 2: Rút gọn biểu thức: \(B =
\frac{sin^{3}\alpha + cos^{3}\alpha}{\sin\alpha + \cos\alpha} +
\frac{sin^{3}\alpha - cos^{3}\alpha}{\sin\alpha -
\cos\alpha}.\)
Hướng dẫn giải
Ta có:
\(sin^{3}\alpha + cos^{3}\alpha =
(sin\alpha + \cos\alpha)(sin^{2}\alpha - \sin\alpha\cos\alpha +
cos^{2}\alpha)\)
\(= (sin\alpha + \cos\alpha)(1 -
\sin\alpha\cos\alpha)\)
Suy ra \(\frac{sin^{3}\alpha +
cos^{3}\alpha}{\sin\alpha + \cos\alpha} = \frac{(sin\alpha +
\cos\alpha)(1 - \sin\alpha\cos\alpha)}{(sin\alpha + \cos\alpha)} = 1 -
\sin\alpha\cos\alpha\)
Tương tự: \(\frac{sin^{3}\alpha -
cos^{3}\alpha}{\sin\alpha - \cos\alpha} = \frac{(sin\alpha -
\cos\alpha)(1 + \sin\alpha\cos\alpha)}{(sin\alpha - \cos\alpha)} = 1 +
\sin\alpha\cos\alpha\)
Do đó \(B = (1 - \sin\alpha\cos\alpha) + (1
+ \sin\alpha\cos\alpha) = 2\)
Vậy \(B = 2.\)
Ví dụ 3: Đơn giản các biểu thức:
a) \(E = cos^{2}a +
cos^{2}a.cot^{2}a\) b) \(F = sin^{2}a +
sin^{2}a.tan^{2}a\)
c) \(G = \frac{2cos^{2}a - 1}{\sin a + \cos
a}\) d) \(H = \sqrt{sin^{2}a.(1 + \cot
a) + cos^{2}a.(1 + \tan a)}\)
Hướng dẫn giải
a) Ta có:
\(E = cos^{2}a + cos^{2}a.cot^{2}a =
cos^{2}a.(1 + cot^{2}a)\)
\(E = cos^{2}a.\frac{1}{sin^{2}a} =
cot^{2}a\).
b) Ta có:
\(F = sin^{2}a + sin^{2}a.tan^{2}a =
sin^{2}a.(1 + tan^{2}a)\)
\(F = sin^{2}a.\frac{1}{cos^{2}a} =
tan^{2}a\).
c) Ta có:
\(G = \frac{2cos^{2}a - 1}{\sin a + \cos
a} = \frac{2cos^{2}a - cos^{2}a - sin^{2}a}{\sin a + \cos
a}\)
\(G = \frac{cos^{2}a - sin^{2}a}{\sin a +
\cos a} = \frac{(cosa + \sin a).(cosa - \sin a)}{\sin a + \cos
a}\)
\(G = \cos a - \sin a\).
d) Ta có:
\(H = \sqrt{sin^{2}a.\left( 1 + \frac{\cos
a}{\sin a} \right) + cos^{2}a.\left( 1 + \frac{\sin a}{\cos a}
\right)}\)
\(H = \sqrt{sin^{2}a + \sin a.cosa +
cos^{2}a + \sin a.cosa}\)
\(H = \sqrt{(sina + \cos a)^{2}}
\Rightarrow H = \left| \sin a + \cos a \right|\)
Bạn muốn xem toàn bộ tài liệu? Hãy nhấn Tải về ngay
--------------------------------------------------------
Qua bài viết Rút gọn biểu thức lượng giác Toán 10, hy vọng các em đã nắm được cách sử dụng công thức lượng giác cơ bản và phương pháp rút gọn nhanh để xử lý các dạng bài tập. Hãy ôn luyện thường xuyên để củng cố kiến thức về giá trị lượng giác của góc từ 0 đến 180 độ, giúp tự tin chinh phục các đề thi và bài kiểm tra Toán 10.
