Tìm độ dài của tổng của hai hay nhiều vectơ Toán 10
Cách tìm độ dài của tổng vectơ
Tìm độ dài của tổng của hai hay nhiều vectơ là dạng bài tập quan trọng trong chương trình Toán 10 – chuyên đề Vectơ, giúp học sinh hiểu rõ mối liên hệ giữa các vectơ và ứng dụng của quy tắc hình bình hành trong hình học. Bài viết dưới đây sẽ hướng dẫn chi tiết cách xác định độ dài của tổng các vectơ, kèm theo ví dụ minh họa và đáp án chi tiết, giúp bạn nắm vững kiến thức và vận dụng hiệu quả trong các bài kiểm tra và kỳ thi THPT.
A. Phương pháp giải
Dùng quy tắc ba điểm và quy tắc hình bình hành.
Quy tắc ba điểm
Cho A, B ,C tùy ý, ta có : 
\(\overrightarrow{AB} + \overrightarrow{BC} =
\overrightarrow{AC}\)
Quy tắc hình bình hành
Nếu \(ABCD\) là hình bình hành thì \(\overrightarrow{AB} + \overrightarrow{AD} =
\overrightarrow{AC}\)
Quy tắc về hiệu vectơ
Cho O , A , B tùy ý ta có : \(\overrightarrow{OB}\ - \ \overrightarrow{OA}\ =
\ \overrightarrow{AB}\)
Chú ý: Ta có thể mở rộng quy tắc ba điểm cho n điểm \(A_{1},\ A_{2},\ ...,\ A_{n}\) thì:
\(\overrightarrow{A_{1}A_{2}} +
\overrightarrow{A_{2}A_{3}} + ... + \overrightarrow{A_{n - 1}A_{n}} =
\overrightarrow{A_{1}A_{n}}\)
B. Ví dụ minh họa tìm độ dài của hai hay nhiều vectơ
Ví dụ 1: Cho hình vuông \(ABCD\) tâm \(O\) có cạnh bằng \(3\).
a) Tìm \(\left| \overrightarrow{AD} +
\overrightarrow{AB} \right|\) b) Tìm \(\left| \overrightarrow{AB} + \overrightarrow{OD}
\right|\)
Hướng dẫn giải
Hình vẽ minh họa:
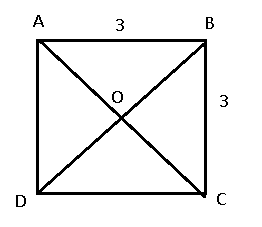
a. Theo quy tắc đường chéo hình bình hành, ta có:
\(\left| \overrightarrow{AD} +
\overrightarrow{AB} \right| = \left| \overrightarrow{AC} \right| = AC =
AB\sqrt{2} = 3\sqrt{2}\).
b. Ta có:
\(\overrightarrow{AB} +
\overrightarrow{OD} = \overrightarrow{AB} + \overrightarrow{BO} =
\overrightarrow{AO}\)
\(\Rightarrow \left| \overrightarrow{AB} +
\overrightarrow{OD} \right| = \left| \overrightarrow{AO} \right| = OA =
\frac{1}{2}AC = \frac{3\sqrt{2}}{2}\)
Ví dụ 2: Cho hình chữ nhật \(ABCD\) có cạnh bằng \(AB = a;\ AD =
a\sqrt{2}.\). Tìm độ dài của các vectơ:
a) \(\overrightarrow{DC} +
\overrightarrow{BD} + \overrightarrow{AB}\) b) \(\overrightarrow{AB} +
\overrightarrow{AC}\)
Hướng dẫn giải
a) Ta có:
\(\overrightarrow{DC} + \overrightarrow{BD}
+ \overrightarrow{AB} = \overrightarrow{AB} + \overrightarrow{BD} +
\overrightarrow{DC} = \overrightarrow{AC}\)
\(\left| \overrightarrow{DC} +
\overrightarrow{BD} + \overrightarrow{AB} \right| = \left|
\overrightarrow{AC} \right| = AC = \sqrt{a^{2} + (a\sqrt{2})^{2}} =
a\sqrt{3}\)
b) Dựng hình bình hành \(ABEC\), khi đó ta có:
\(\overrightarrow{AB} + \overrightarrow{AC}
= \overrightarrow{AE}\)
\(\Rightarrow \left| \overrightarrow{AB} +
\overrightarrow{AC} \right| = \left| \overrightarrow{AE} \right| =
AE.\)
Gọi \(I\) là trung điểm của \(CB,\) khi đó:
\(AE
= 2AI = 2\sqrt{AB^{2} + BI^{2}} = 2\sqrt{a^{2} +
(\frac{a\sqrt{3}}{2})^{2}} = a\sqrt{7}.\)
Vậy \(\left| \overrightarrow{AB} +
\overrightarrow{AC} \right| = a\sqrt{7}.\)
Ví dụ 3: Cho lục giác đều\(ABCDEF\) và \(O\) là tâm của nó. Tìm độ dài của
a) \(\overrightarrow{AB} +
\overrightarrow{OE}\). b) \(\overrightarrow{AB} + \overrightarrow{CD} +
\overrightarrow{EF}\)
Hướng dẫn giải
Hình vẽ minh họa:
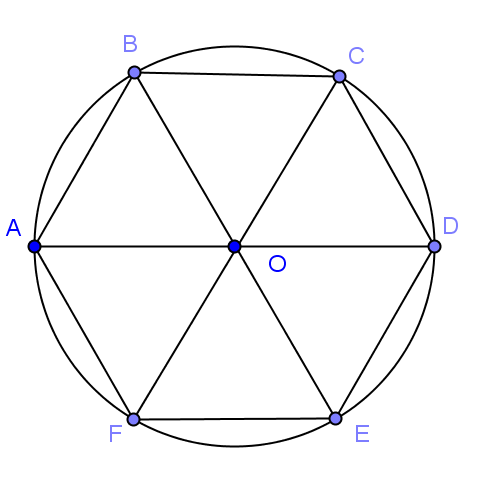
a) Ta có:
\(\overrightarrow{AB} + \overrightarrow{OE}
= \overrightarrow{FO} + \overrightarrow{OE} =
\overrightarrow{FE}.\)
\(\left| \overrightarrow{AB} +
\overrightarrow{OE} \right| = \left| \overrightarrow{FE} \right| =
1.\)
b) Ta có
\(\overrightarrow{AB} +
\overrightarrow{CD} + \overrightarrow{EF} = \overrightarrow{AB} +
\overrightarrow{BO} + \overrightarrow{OA} =
\overrightarrow{0}\)
\(\Rightarrow \left| \overrightarrow{AB} +
\overrightarrow{CD} + \overrightarrow{EF} \right| = 0.\)
Ví dụ 4: Cho tam giác đều \(ABC\) cạnh \(5\). Tìm \(\left| \overrightarrow{AB} + \overrightarrow{AC}
\right|\)?
Hướng dẫn giải
Hình vẽ minh họa:
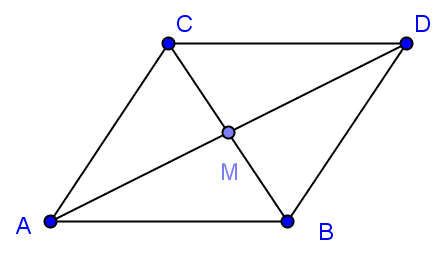
Dựng hình bình hành \(ABDC\) và gọi \(M\) là trung điểm của \(BC\).
Ta có
\(\overrightarrow{AB} +
\overrightarrow{AC} = \overrightarrow{AD}\)
\(\Rightarrow \left| \overrightarrow{AB} +
\overrightarrow{AC} \right| = \left| \overrightarrow{AD} \right| = AD =
2AM.\)
Tam giác \(ABC\) đều nên \(AM\bot BC.\)
\(AM = \sqrt{AB^{2} - BM^{2}} =
\sqrt{5^{2} - \left( \frac{5}{2} \right)^{2}} =
\frac{5\sqrt{3}}{2}.\)
Vậy \(\left| \overrightarrow{AB} +
\overrightarrow{AC} \right| = 2AM = 2.\frac{5\sqrt{3}}{2} =
5\sqrt{3}.\).
C. Bài tập tự rèn luyện tính độ dài tổng các vectơ có đáp án
Bài tập 1: Cho hình thoi \(ABCD\) với cạnh có độ dài bằng \(3\) và \(\widehat{BAD} = 120^{0}\). Tính độ dài của các vectơ:
a) \(\overrightarrow{CB} +
\overrightarrow{CD}\) b) \(\overrightarrow{DB} + \overrightarrow{CD} +
\overrightarrow{BA}\)
Bài tập 2: Cho hình thang \(ABCD\) có \(AB\) song song với \(CD\). Cho \(AB =
2a;CD = a\). Gọi \(O\) là trung điểm của \(AD\). Tìm \(\left| \overrightarrow{OB} + \overrightarrow{OC}
\right|\)?
Bài tập 3. Cho tam giác \(ABC\) đều cạnh \(a\). Khi đó \(\left| \overrightarrow{AB} + \overrightarrow{AC}
\right|\) bằng:
A. \(\left| \overrightarrow{AB} +
\overrightarrow{AC} \right| = a\sqrt{3}.\) B. \(\left| \overrightarrow{AB} + \overrightarrow{AC}
\right| = \frac{a\sqrt{3}}{2}.\)
C. \(\left| \overrightarrow{AB} +
\overrightarrow{AC} \right| = 2a.\) D. Một đáp án khác.
Bài tập 4. Cho tam giác vuông cân \(ABC\) tại \(A\) có \(AB =
a\). Tính \(\left| \overrightarrow{AB}
+ \overrightarrow{AC} \right|.\)
A. \(\left| \overrightarrow{AB} +
\overrightarrow{AC} \right| = a\sqrt{2}.\) B. \(\left| \overrightarrow{AB} + \overrightarrow{AC}
\right| = \frac{a\sqrt{2}}{2}.\)
C. \(\left| \overrightarrow{AB} +
\overrightarrow{AC} \right| = 2a.\) D. \(\left| \overrightarrow{AB} + \overrightarrow{AC}
\right| = a.\)
Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!
-----------------------------------------------------------
Qua bài viết này, bạn đã nắm vững cách tìm độ dài của tổng của hai hay nhiều vectơ Toán 10 bằng các công thức và phương pháp hình học cơ bản. Việc hiểu rõ quy tắc cộng vectơ không chỉ giúp giải nhanh các dạng bài tập trong chuyên đề Vectơ Toán 10, mà còn là nền tảng quan trọng cho các chương kiến thức cao hơn như hình học không gian hay lượng giác.
👉 Hãy luyện tập thêm nhiều bài tập vectơ có đáp án chi tiết để củng cố kỹ năng và đạt kết quả tốt nhất trong các kỳ kiểm tra, thi học kỳ và thi THPT Quốc gia.
