Tìm tổng của hai vectơ và tổng của nhiều vectơ
Cách xác định tổng của hai vectơ, tổng của nhiều vectơ
Trong chương trình Toán 10, phần vectơ là một chuyên đề quan trọng giúp học sinh hiểu rõ mối liên hệ giữa hình học và đại số. Trong đó, việc tìm tổng của hai vectơ và tổng của nhiều vectơ đóng vai trò nền tảng để học tốt các nội dung tiếp theo như chứng minh đẳng thức vectơ, quy tắc hình bình hành và tọa độ vectơ.
Bài viết dưới đây sẽ hướng dẫn chi tiết cách xác định tổng của hai vectơ, tổng của nhiều vectơ, cùng các ví dụ minh họa và bài tập có lời giải giúp bạn dễ hiểu – dễ nhớ – dễ áp dụng trong bài thi và luyện tập.
A. Phương pháp giải bài toán
Áp dụng quy tắc 3 điểm, hình bình hành và tính chất
Quy tắc ba điểm
Với ba điểm bất kỳ 
\(A,\ B,\ C\) ta có \(\overrightarrow{AB} = \overrightarrow{AC}
+ \overrightarrow{CB}\)
Quy tắc hình bình hành
Cho \(ABCD\) là hình bình hành khi đó ta có \(\left\lbrack \begin{matrix}
\overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{AD} \\
\overrightarrow{DB} = \overrightarrow{DA} + \overrightarrow{DG}
\end{matrix} \right.\)và \(\left\lbrack \begin{matrix}
\overrightarrow{AB} = \overrightarrow{DC} \\
\overrightarrow{AD} = \overrightarrow{BC}
\end{matrix} \right.\).
Tính chất
- Giao hoán: \(\overrightarrow{a} +
\overrightarrow{b} = \overrightarrow{b} +
\overrightarrow{a}\)
- Kết hợp: \(\overrightarrow{a} + \left(
\overrightarrow{b} + \overrightarrow{c} \right) = \left(
\overrightarrow{a} + \overrightarrow{c} \right) +
\overrightarrow{b}\)
- Cộng với vectơ đối: \(\overrightarrow{a}
+ \left( - \overrightarrow{a} \right) = \overrightarrow{0}\)
- Cộng với vectơ không: \(\overrightarrow{a} + \overrightarrow{0} =
\overrightarrow{0} + \overrightarrow{a} =
\overrightarrow{a}\)
B. Ví dụ minh họa Tìm tổng của hai hay nhiều vectơ
Ví dụ 1: a) Cho bốn điểm \(A,B,C,D\) tùy ý. Tìm tổng của các vectơ: \(\overrightarrow{u} = \overrightarrow{DC} +
\overrightarrow{AB} + \overrightarrow{BD}\)
b) Cho các điểm \(M,N,P,Q,R\) tùy ý. Tìm tổng của các vectơ:
\(\overrightarrow{v} =
\overrightarrow{MN} + \overrightarrow{PQ} + \overrightarrow{R N} +
\overrightarrow{NP} + \overrightarrow{QR}\)
Hướng dẫn giải
a) Ta có:
\(\overrightarrow{u} = \overrightarrow{DC}
+ \overrightarrow{AB} + \overrightarrow{BD} = \overrightarrow{DC} +
\overrightarrow{AD} = \overrightarrow{AD} + \overrightarrow{DC} =
\overrightarrow{AC}\)
b) Ta có:
\(\overrightarrow{v} = \overrightarrow{MN}
+ \overrightarrow{PQ} + \overrightarrow{R N} + \overrightarrow{NP} +
\overrightarrow{QR}\)
\(= \left( \overrightarrow{MN} +
\overrightarrow{NP} + \overrightarrow{PQ} + \overrightarrow{QR} +
\overrightarrow{RN} \right) = \overrightarrow{MN}\)
Ví dụ 2: Cho tứ giác \(ABCD\). Chứng minh rằng:
a) \(\overrightarrow{AB} +
\overrightarrow{BC} + \overrightarrow{CD} + \overrightarrow{DA} =
\overrightarrow{0}.\) b) \(\overrightarrow{AB} +
\overrightarrow{CD} = \overrightarrow{AD} +
\overrightarrow{CB}\)
Hướng dẫn giải
a) Ta có
\(\overrightarrow{AB} +
\overrightarrow{BC} + \overrightarrow{CD} +
\overrightarrow{DA}\)
\(= (\overrightarrow{AB} +
\overrightarrow{BC}) + (\overrightarrow{CD} +
\overrightarrow{DA})\)
\(= \overrightarrow{AC} +
\overrightarrow{CA} = \overrightarrow{AA} =
\overrightarrow{0}.\)
b) Ta có
\(\overrightarrow{AB} + \overrightarrow{CD}
= \overrightarrow{AD} + \overrightarrow{DB} + \overrightarrow{CB} +
\overrightarrow{BD}\)
\(= \overrightarrow{AD} +
\overrightarrow{CB} + \overrightarrow{DB} +
\overrightarrow{BD}\)
\(= \overrightarrow{AD} +
\overrightarrow{CB} + \overrightarrow{DD} = \overrightarrow{AD} +
\overrightarrow{CB} + \overrightarrow{0}\)
\(= \overrightarrow{AD} +
\overrightarrow{CB}.\)
Ví dụ 3: Cho 6 điểm \(A,B,C,D,E,F\). Chứng minh rằng:
a) \(\overrightarrow{AB} +
\overrightarrow{CD} + \overrightarrow{FA} + \overrightarrow{BC} +
\overrightarrow{EF} + \overrightarrow{DE} =
\overrightarrow{0}\).
b) \(\overrightarrow{AD} +
\overrightarrow{BE} + \overrightarrow{CF} = \overrightarrow{AE} +
\overrightarrow{BF} + \overrightarrow{CD}\)
Hướng dẫn giải
a) Ta có:
\(\overrightarrow{AB} +
\overrightarrow{CD} + \overrightarrow{FA} + \overrightarrow{BC} +
\overrightarrow{EF} + \overrightarrow{DE}\)
\(= \overrightarrow{AB} +
\overrightarrow{BC} + \overrightarrow{CD} + \overrightarrow{DE} +
\overrightarrow{EF} + \overrightarrow{FA} =
\overrightarrow{0}\)
b) Ta có:
\(\overrightarrow{AD} + \overrightarrow{BE}
+ \overrightarrow{CF}\) \(=
\overrightarrow{AE} + \overrightarrow{ED} + \overrightarrow{BF} +
\overrightarrow{FE} + \overrightarrow{CD} +
\overrightarrow{DF}\)
\(= \overrightarrow{AE} +
\overrightarrow{BF} + \overrightarrow{CD} + \overrightarrow{FE} +
\overrightarrow{ED} + \overrightarrow{DF}\)
\(= \overrightarrow{AE} +
\overrightarrow{BF} + \overrightarrow{CD} + \overrightarrow{FD} +
\overrightarrow{DF}\)
\(= \overrightarrow{AE} +
\overrightarrow{BF} + \overrightarrow{CD} + \overrightarrow{0} =
\overrightarrow{AE} + \overrightarrow{BF} +
\overrightarrow{CD}.\)
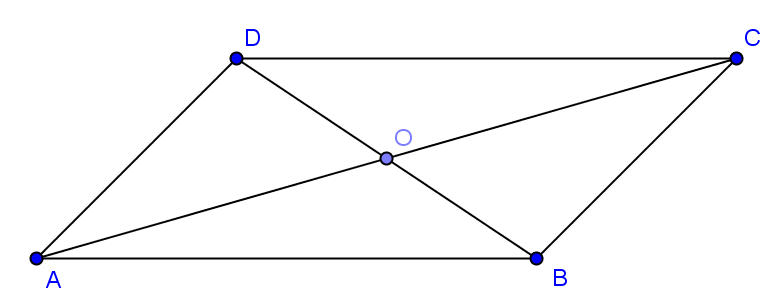
Ví dụ 4: Cho hình bình hành \(ABCD\)tâm \(O\). Chứng minh rằng
a) \(\overrightarrow{AB} +
\overrightarrow{CD} = \overrightarrow{0}\)
b) \(\overrightarrow{DO} +
\overrightarrow{AO} = \overrightarrow{AB}\)
c) \(\overrightarrow{OA} +
\overrightarrow{OB} + \overrightarrow{OC} + \overrightarrow{OD} =
\overrightarrow{0}\)
d) Với \(M\) là điểm bất kì, hãy chứng minh: \(\overrightarrow{MA} +
\overrightarrow{MC} = \overrightarrow{MB} +
\overrightarrow{MD}.\)
e) Với \(E\) là điểm bất kì, hãy chứng minh: \(\overrightarrow{AB} +
\overrightarrow{CE} + \overrightarrow{AD} =
\overrightarrow{AE}.\)
Hướng dẫn giải
Hình vẽ minh họa:
a) Ta có: \(\overrightarrow{CD} =
\overrightarrow{BA}\).
Do đó: \(\overrightarrow{AB} + \overrightarrow{CD} =
\overrightarrow{AB} + \overrightarrow{BA} = \overrightarrow{AA} =
\overrightarrow{0}.\)
Vậy \(\overrightarrow{AB} +
\overrightarrow{CD} = \overrightarrow{0}\)
b) Ta có: \(\overrightarrow{DO} =
\overrightarrow{OB}\).
Do đó \(\overrightarrow{DO} + \overrightarrow{AO} =
\overrightarrow{OB} + \overrightarrow{AO} = \overrightarrow{AO} +
\overrightarrow{OB} = \overrightarrow{AB}.\)
Vậy \(\overrightarrow{DO} +
\overrightarrow{AO} = \overrightarrow{AB}\)
c) Ta có: Ví \(O\) là trung điểm của \(AC\) và \(BD\) nên \(\overrightarrow{OA} + \overrightarrow{OC} =
\overrightarrow{0};\ \ \ \overrightarrow{OB} + \overrightarrow{OD} =
\overrightarrow{0}.\)
Do đó: \(\overrightarrow{OA} +\overrightarrow{OB} + \overrightarrow{OC} + \overrightarrow{OD}\)
\(= \left(\overrightarrow{OA} + \overrightarrow{OC} \right) + \left(\overrightarrow{OB} + \overrightarrow{OD} \right)\)\(= \overrightarrow{0} +\overrightarrow{0} = \overrightarrow{0}.\)
d) Ta có
\(\overrightarrow{MA} + \overrightarrow{MC}
= \overrightarrow{MB} + \overrightarrow{BA} + \overrightarrow{MD} +
\overrightarrow{DC}\)
\(= \overrightarrow{MB} +
\overrightarrow{MD} + \overrightarrow{BA} + \overrightarrow{DC} =
\overrightarrow{MB} + \overrightarrow{MD} + \overrightarrow{BA} +
\overrightarrow{BA}\)
\(= \overrightarrow{MB} +
\overrightarrow{MD} + \overrightarrow{0} = \overrightarrow{MB} +
\overrightarrow{MD}.\)
Vậy \(\overrightarrow{MA} +
\overrightarrow{MC} = \overrightarrow{MB} +
\overrightarrow{MD}.\)
e) Ta có: \(\overrightarrow{AB} +
\overrightarrow{AD} = \overrightarrow{AC}.\)
Do đó \(\overrightarrow{AB} +
\overrightarrow{CE} + \overrightarrow{AD} = \overrightarrow{AB} +
\overrightarrow{AD} + \overrightarrow{CE} = \overrightarrow{AC} +
\overrightarrow{CE} = \overrightarrow{AE}.\)
Vậy \(\overrightarrow{AB} +
\overrightarrow{CE} + \overrightarrow{AD} =
\overrightarrow{AE}.\)
B. Bài tập tự rèn luyện tính độ dài của tổng các vectơ
Bài tập 1: Cho bốn điểm \(A,\ B,\ C,\
D\) bất kì. Chứng minh rằng: nếu \(\overrightarrow{AB} = \overrightarrow{CD}\) thì \(\overrightarrow{AC} =
\overrightarrow{BD}\).
Bài tập 2. Cho lục giác đều\(ABCDEF\) và \(O\) là tâm của nó. Chứng minh rằng
a) \(\overrightarrow{OA} +
\overrightarrow{OB} + \overrightarrow{OC} + \overrightarrow{OD} +
\overrightarrow{OE} + \overrightarrow{OF} =
\overrightarrow{0}\).
b) \(\overrightarrow{AB} +
\overrightarrow{CD} + \overrightarrow{FE} =
\overrightarrow{AD}.\)
c) \(\overrightarrow{OA} +
\overrightarrow{OC} + \overrightarrow{OB} =
\overrightarrow{EB}.\)
Bài tập 3. Cho tam giác \(ABC\). Gọi \(M\), \(N\), \(P\) lần lượt là trung điểm của \(BC\), \(CA\), \(AB\). Chứng minh rằng:
a) \(\overrightarrow{PB} +
\overrightarrow{MC} = \overrightarrow{AN}\)
b)\(\overrightarrow{BM} +
\overrightarrow{CN} + \overrightarrow{AP} =
\overrightarrow{0}\).
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu.
----------------------------------------------------------
Kiến thức về tổng của hai vectơ và tổng của nhiều vectơ giúp học sinh hiểu sâu hơn về phép cộng vectơ, đồng thời hỗ trợ mạnh mẽ trong chứng minh đẳng thức vectơ và các dạng bài toán hình học phẳng.
👉 Qua bài viết này, bạn đã nắm được công thức, quy tắc tính và phương pháp giải chi tiết để vận dụng thành thạo trong mọi dạng bài.
