Tìm tổng hoặc hiệu của hai vectơ hay nhiều vectơ
Chuyên đề Toán 10: Tính tổng hoặc hiệu vectơ có đáp án
Trong chương trình Toán 10, việc tìm tổng hoặc hiệu của hai vectơ hay nhiều vectơ là kiến thức cơ bản nhưng đóng vai trò quan trọng trong việc chứng minh các đẳng thức vectơ và giải các bài toán hình học. Bài viết dưới đây sẽ hướng dẫn chi tiết quy tắc cộng, trừ vectơ, cách biểu diễn và vận dụng vào các bài tập minh họa có lời giải, giúp bạn nắm vững nền tảng và áp dụng hiệu quả trong học tập.
A. Phương pháp giải toán
- Áp dùng định nghĩa: Tìm vectơ đối, tính tổng
- Áp dụng quy tắc 3 điểm, hình bình hành và tính chất
B. Ví dụ minh họa tính tổng, hiệu các vectơ
Ví dụ 1: Tìm tổng của các vectơ
a) Cho ba điểm 
\(B,C,O\) tùy ý. Tìm tổng của vectơ \(\overrightarrow{u} =
\overrightarrow{OC} - \overrightarrow{OB}\)
b) Cho bốn điểm \(A,B,C,D\) tùy ý Tìm tổng của vectơ \(\overrightarrow{v} =
\overrightarrow{AB} + \overrightarrow{CD} -
\overrightarrow{AD}\)
c) Cho các điểm \(M,N,P,Q,R\) tùy ý Tìm tổng của vectơ \(\overrightarrow{a} =
\overrightarrow{MN} - \overrightarrow{QP} + \overrightarrow{RN} -
\overrightarrow{PN} + \overrightarrow{QR}\)
Hướng dẫn giải
a) Áp dụng quy tắc ba điểm với phép trừ vectơ ta được
\(\overrightarrow{u} = \overrightarrow{OC}
- \overrightarrow{OB} = \overrightarrow{BC}\)
b) Ta có: \(\overrightarrow{AB} +
\overrightarrow{CD} - \overrightarrow{AD}\)
\(= \overrightarrow{AB} -
\overrightarrow{AD} + \overrightarrow{CD} = \overrightarrow{DB} +
\overrightarrow{CD} = \overrightarrow{CB}\).
c) Ta có: \(\overrightarrow{a} =
\overrightarrow{MN} - \overrightarrow{QP} + \overrightarrow{RN} -
\overrightarrow{PN} + \overrightarrow{QR} = \overrightarrow{MN} +
\overrightarrow{NP} + \overrightarrow{PQ} + \overrightarrow{QR} +
\overrightarrow{RN} = \overrightarrow{MN}.\).
Ví dụ 2: Cho các điểm phân biệt\(A,\ B,\
C,\ D\). Chứng mình rằng:
a) \(\overrightarrow{AB} +
\overrightarrow{CD} = \overrightarrow{AD} +
\overrightarrow{CB}\) b) \(\overrightarrow{AB} -
\overrightarrow{AD} = \overrightarrow{DC} -
\overrightarrow{BC}\)
Hướng dẫn giải
a) Cách 1: Phần tổng hai vectơ
Cách 2: Ta có:
\(\begin{matrix}
\overrightarrow{AB} + \overrightarrow{CD} = \overrightarrow{AD} +
\overrightarrow{CB}\ \ \ \ (1) \\
\Leftrightarrow \overrightarrow{AB} - \overrightarrow{AD} =
\overrightarrow{CB} - \overrightarrow{CD} \Leftrightarrow
\overrightarrow{DB} = \overrightarrow{DB}\ \ (2)
\end{matrix}\)
Cách 3: Ta có
\(\begin{matrix}
\overrightarrow{AB} + \overrightarrow{CD} = \overrightarrow{OB} -
\overrightarrow{OA} + \overrightarrow{OD} - \overrightarrow{OC},\
\forall O. \\
= \overrightarrow{OD} - \overrightarrow{OA} + \overrightarrow{OB} -
\overrightarrow{OC} = \overrightarrow{AD} + \overrightarrow{CB}
\end{matrix}\)
Vì (2) luôn đúng với mọi \(A,\ B,\ C,\
D\) nên (1) đúng.
Vậy \(\overrightarrow{AB} +
\overrightarrow{CD} = \overrightarrow{AD} +
\overrightarrow{CB}\)
b) Ta có: \(\overrightarrow{AB} -
\overrightarrow{AD} = \overrightarrow{DB},\ \overrightarrow{DC} -
\overrightarrow{BC} = \overrightarrow{DC} + \overrightarrow{CB} =
\overrightarrow{DB}\).
Vậy: \(\overrightarrow{AB} -
\overrightarrow{AD} = \overrightarrow{DC} -
\overrightarrow{BC}\).
Ví dụ 3: Cho hình bình hành \(ABCD\) có tâm \(O\). Chứng minh rằng:
a) \(\overrightarrow{CO} -
\overrightarrow{OB} = \overrightarrow{CD}\) b) \(\overrightarrow{AB} -
\overrightarrow{AC} = \overrightarrow{DA}\)
c) \(\overrightarrow{AB} -
\overrightarrow{BC} = \overrightarrow{DB}\) d) \(\overrightarrow{DA} -
\overrightarrow{DB} = \overrightarrow{OD} -
\overrightarrow{OC}\)
e) \(\overrightarrow{DA} -
\overrightarrow{DB} + \overrightarrow{DC} =
\overrightarrow{0}\)
f) \(M\) là một điểm tùy ý. Hãy chứng minh \(\overrightarrow{MA} -
\overrightarrow{MB} = \overrightarrow{AB} - \overrightarrow{AC} +
\overrightarrow{BD}\).
Hướng dẫn giải
Hình vẽ minh họa:
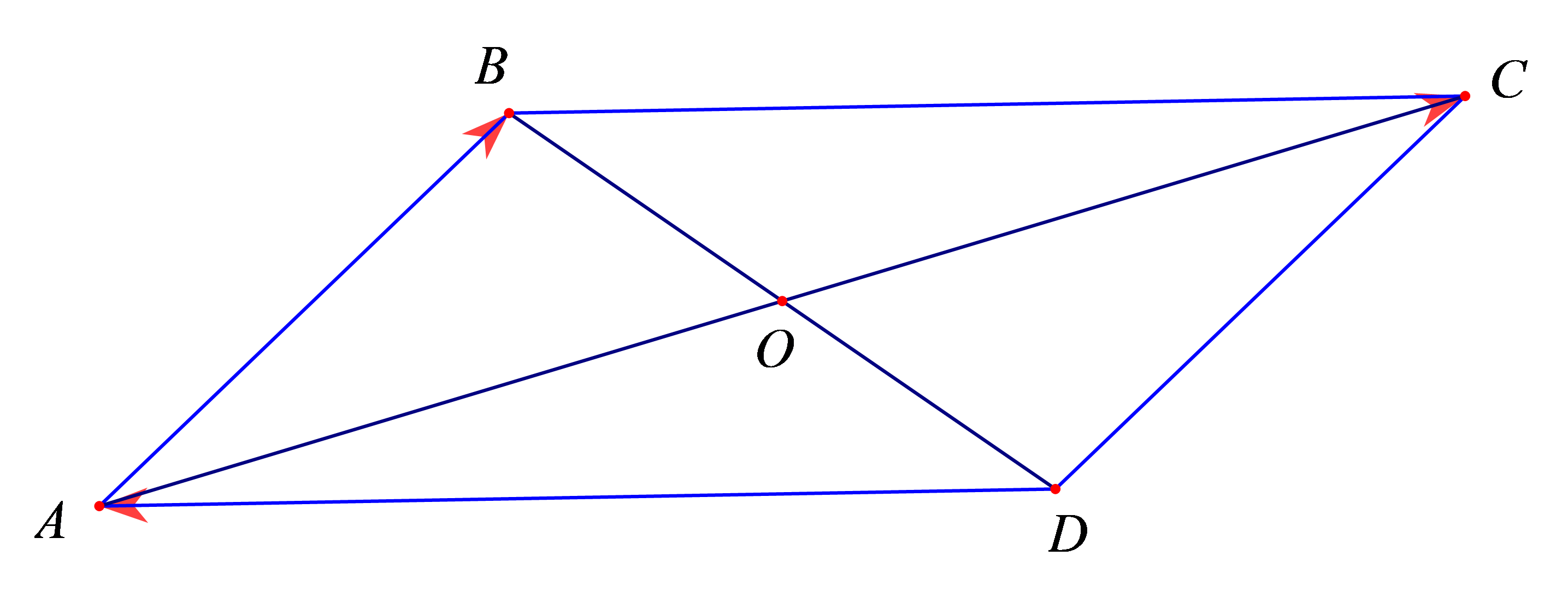
a) Ta có: \(\overrightarrow{CO} -
\overrightarrow{OB} = \overrightarrow{OA} - \overrightarrow{OB} =
\overrightarrow{BA}\)
Do \(ABCD\) là hình bình hành nên \(\overrightarrow{BA} =
\overrightarrow{CD}\) . Vậy \(\overrightarrow{CO} - \overrightarrow{OB} =
\overrightarrow{CD}\).
b) Ta có \(\overrightarrow{AB} -
\overrightarrow{AC} = \overrightarrow{CB}\).
Do \(ABCD\) là hình bình hành nên \(\overrightarrow{CB} =
\overrightarrow{DA}\) nên \(\overrightarrow{AB} - \overrightarrow{AC} =
\overrightarrow{DA}\).
c) Vì \(ABCD\) là hình bình hành nên \(\overrightarrow{BC} =
\overrightarrow{AD}\). Do đó \(\overrightarrow{AB} - \overrightarrow{BC} =
\overrightarrow{AB} - \overrightarrow{AD} =
\overrightarrow{DB}.\)
d) Ta có: \(\overrightarrow{DA} -
\overrightarrow{DB} = \overrightarrow{BA};\overrightarrow{OD} -
\overrightarrow{OC} = \overrightarrow{CD}\)
Vì \(ABCD\) là hình bình hành nên \(\overrightarrow{BA} =
\overrightarrow{CD}\). Suy ra \(\overrightarrow{DA} - \overrightarrow{DB} =
\overrightarrow{OD} - \overrightarrow{OC}\)
e) Ta có: \(\overrightarrow{DA} -
\overrightarrow{DB} + \overrightarrow{DC} = \overrightarrow{BA} +
\overrightarrow{DC} = \overrightarrow{BA} + \overrightarrow{AB} =
\overrightarrow{0}\)
f) Ta có:
\(\overrightarrow{MA} -
\overrightarrow{MB} = \overrightarrow{BA}\)
\(\overrightarrow{AB} -
\overrightarrow{AC} + \overrightarrow{BD} = \overrightarrow{CB} +
\overrightarrow{BD} = \overrightarrow{CD}\)
Vì \(ABCD\) là hình bình hành nên \(\overrightarrow{BA} =
\overrightarrow{CD}\).
Vậy \(\overrightarrow{MA} -
\overrightarrow{MB} = \overrightarrow{AB} - \overrightarrow{AC} +
\overrightarrow{BD}\).
C. Bài tập tự rèn luyện có đáp án tham khảo chi tiết
Bài tập 1. Cho năm điểm \(A,\ B,\ C,\ D,\
E\). Chứng minh rằng:
a) \(\overrightarrow{AB} +
\overrightarrow{CD} + \overrightarrow{EA} = \overrightarrow{CB} +
\overrightarrow{ED}\) b) \(\overrightarrow{AC} +
\overrightarrow{CD} - \overrightarrow{EC} = \overrightarrow{AE} -
\overrightarrow{DB} + \overrightarrow{CB}\)
Bài tập 2: Cho hình bình hành \(ABCD\) tâm \(O\). M là một điểm bất kì trong mặt phẳng. Chứng minh rằng:
a) \(\overrightarrow{BA} +
\overrightarrow{DA} + \overrightarrow{AC} =
\overrightarrow{0}\) b) \(\overrightarrow{OA} +
\overrightarrow{OB} + \overrightarrow{OC} + \overrightarrow{OD} =
\overrightarrow{0}\)
c) \(\overrightarrow{MA} +
\overrightarrow{MC} = \overrightarrow{MB} + \overrightarrow{MD}\) .
Bài tập 3. Cho tam giác \(ABC\). Gọi M, N, P lần lượt là trung điểm của \(BC,\ \
CA,\ \ AB\). Chứng minh rằng:
a) \(\overrightarrow{BM} +
\overrightarrow{CN} + \overrightarrow{AP} =
\overrightarrow{0}\) b) \(\overrightarrow{AP} +
\overrightarrow{AN} - \overrightarrow{AC} + \overrightarrow{BM} =
\overrightarrow{0}\)
Bạn muốn xem toàn bộ tài liệu? Hãy nhấn Tải về ngay!
-----------------------------------------------
Như vậy, qua bài viết này, bạn đã hiểu rõ cách tìm tổng hoặc hiệu của hai vectơ hay nhiều vectơ cùng phương pháp chứng minh đẳng thức vectơ một cách logic và dễ nhớ. Kiến thức này không chỉ quan trọng trong chuyên đề Vectơ Toán 10, mà còn là bước đệm vững chắc cho các chương trình học nâng cao.
