Tính độ dài cạnh còn lại của tam giác khi biết hai cạnh và góc xen giữa
Giải bài tập hệ thức lượng trong tam giác có đáp án
Trong chương trình Toán 10, chuyên đề Hệ thức lượng trong tam giác là phần kiến thức quan trọng giúp học sinh hiểu rõ mối quan hệ giữa các cạnh và góc trong tam giác. Bài viết Tính độ dài cạnh còn lại của tam giác khi biết hai cạnh và góc xen giữa sẽ hướng dẫn chi tiết cách áp dụng định lý cos để tìm cạnh còn lại, kèm ví dụ minh họa và lời giải chi tiết. Đây là tài liệu hữu ích giúp học sinh nắm vững phương pháp giải nhanh và chính xác các bài toán liên quan đến hệ thức lượng trong tam giác.
A. Phương pháp giải
Dùng định lí Cosin
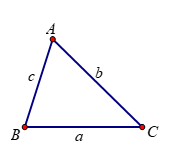
Trong tam giác 
\(ABC\) với \(BC = a,\ \ AC = b\) và \(AB = c\).
|
|
 |
B. Ví dụ minh họa tính độ dài cạnh tam giác khi biết hai cạnh và góc xen giữa
Ví dụ 1: Cho tam giác ABC có \(AB = 2,\ AC = 5\\) và \(\cos A = \frac{4}{5}\). Tính cạnh \(BC\).
Hướng dẫn giải
Ta có:
\(BC^{2} = AB^{2} + AC^{2} -
2AB.AC.cosA\)
\(= 2^{2} + 5^{2} - 2.5.\frac{4}{5} = 21
\Rightarrow BC = \sqrt{21}\)
Ví dụ 2: Cho tam giác \(ABC\) có \(BC = 2\), \(AC = 2\sqrt{2}\), \(\cos(A + B) = - \frac{\sqrt{2}}{2}\). Độ dài cạnh \(AB\) bằng bao nhiêu?
Hướng dẫn giải
Do \(\cos(A + B) = - \frac{\sqrt{2}}{2}\Rightarrow \cos C = \frac{\sqrt{2}}{2}\).
Áp dụng định lý Cosin trong tam giác có:
\(AB^{2} = BC^{2} + AC^{2} -2BC.AC.\cos C\)
\(= 2^{2} + \left( 2\sqrt{2} \right)^{2} -
2.2.2\sqrt{2}.\frac{\sqrt{2}}{2} = 4\) \(\Rightarrow AB = 2\).
Ví dụ 3: Cho tam giác \(ABC\) có ba góc nhọn và có \(AB = 3\), \(BC = 3\sqrt{3}\), \(\sin B = \frac{1}{\sqrt{3}}\). Tìm độ dài cạnh \(AC\) (chính xác đến hàng phần trăm).
Hướng dẫn giải
Ta có \(\cos B > 0\) (vì \(B\) nhọn), do đó:
\(\cos B = \sqrt{1 - \sin^{2}A} = \sqrt{1 -\left( \frac{1}{\sqrt{3}} \right)^{2}} = \frac{\sqrt{6}}{3}\)
Áp dụng định lý côsin trong tam giác có:
\(AC^{2} = AB^{2} + BC^{2} -2AB.BC.\cos B\)
\(AC^{2} = 3^{2} + \left( 3\sqrt{3}
\right)^{2} - 2.3.3\sqrt{3}.\frac{\sqrt{6}}{3} = 36 -
18\sqrt{2}\)
\(\Rightarrow AC \simeq 3,25\).
Ví dụ 4: Tam giác \(ABC\) có \(a = 8\), \(c = 3\), \(\widehat{B} = 60^{0}\). Tính độ dài cạnh \(b\).
Hướng dẫn giải
Ta có:
\(b^{2} = a^{2} + c^{2} - 2ac\cos B = 8^{2}+ 3^{2} - 2.8.3\cos60^{0}\) \(=
49\)
\(\Rightarrow b = 7\).
Ví dụ 5: Trong tam giác \(ABC\) có \(AB = 2\ cm\), \(AC = 1\ cm\), \(\widehat{A} = 60^{0}\). Tính độ dài cạnh \(BC\)
Hướng dẫn giải
Ta có:
\(BC^{2} = AB^{2} + AC^{2} -2AB.AC.\cos A\)
\(\Rightarrow BC^{2} = 2^{2} + 1^{2} -2.2.1.\cos60^{0}\)
\(\Rightarrow BC^{2} = 3\)
Vậy \(BC = \sqrt{3}\ cm\).
C. Bài tập tự rèn luyện có đáp án chi tiết
Bài tập 1: Cho tam giác ABC có \(\widehat{C} = 30^{0}\), cạnh \(a = 8\), cạnh \(b
= 6\). Tính cạnh \(\ c\) ( làm tròn đến hàng phần trăm).
Bài tập 2: Cho hình thoi \(ABCD\) cạnh bằng 1cm và có \(\widehat{BAD} = 60{^\circ}\). Tính độ dài cạnh \(AC\).
Bài tập 3. Cho \(\Delta ABC\) có hai trung tuyến \(BM = 6;\) \(CN = 9\) và hợp với nhau một góc \(120^0\) Tính các cạnh \(\Delta ABC.\)
Bài tập 4: Cho \(\Delta ABC\) có \(\cos A = \frac{5}{9}.\) Điểm \(D\) thuộc cạnh \(BC\) sao cho \(\widehat{ABC} = \widehat{DAC},\) \(DA = 6,\) \(BD =
\frac{16}{3}.\) Tính chu vi \(\Delta
ABC.\)
Bạn muốn xem toàn bộ tài liệu? Hãy nhấn Tải về ngay!
------------------------------------------------
Hy vọng qua bài viết Tính độ dài cạnh còn lại của tam giác khi biết hai cạnh và góc xen giữa, các em đã nắm được cách vận dụng định lý cos trong hệ thức lượng Toán 10 một cách hiệu quả. Hãy luyện tập thêm các bài tập hệ thức lượng trong tam giác có đáp án khác để củng cố kỹ năng và đạt điểm cao trong các kỳ kiểm tra sắp tới!
