Tính tứ phân vị của mẫu số liệu không ghép nhóm: Công thức và ví dụ
Cách tính tứ phân vị trong mẫu số liệu không ghép nhóm
Trong thống kê, tứ phân vị (Quartiles) là công cụ quan trọng giúp chia mẫu số liệu thành bốn phần bằng nhau, từ đó hỗ trợ việc phân tích và đánh giá dữ liệu một cách chính xác hơn. Ở chương trình Toán 10 – Chuyên đề Mẫu số liệu không ghép nhóm, việc tính tứ phân vị không chỉ giúp học sinh nắm vững kiến thức thống kê cơ bản mà còn rèn luyện kỹ năng xử lý số liệu khoa học. Bài viết này sẽ hướng dẫn bạn cách tính tứ phân vị của mẫu số liệu không ghép nhóm, trình bày công thức cụ thể và ví dụ minh họa chi tiết để dễ dàng ôn tập và vận dụng vào bài tập.
A. Cách tính tứ phân vị của mẫu số liệu không ghép nhóm
Để tìm các tứ phân vị của mẫu số liệu có 
\(n\) giá trị, ta làm như sau:
- Sắp xếp mẫu số liệu theo thứ tự không giảm.
- Tìm trung vị. Giá trị này là \(Q_{2}\).
- Tìm trung vị của nửa số liệu bên trái \(Q_{2}\) (không bao gồm \(Q_{2}\) nếu \(n\) lẻ). Giá trị này là \(Q_{1}\).
- Tìm trung vị của nửa số liệu bên phải \(Q_{2}\) (không bao gồm \(Q_{2}\) nếu \(n\) lẻ). Giá trị này là \(Q_{3}\).
- \(Q_{1},\ \ Q_{2},\ \ Q_{3}\) được gọi là các tứ phân vị của mẫu số liệu.
Chú ý. \(Q_{1}\) được gọi là tứ phân vị thứ nhất hay tứ phân vị dưới, \(Q_{3}\) được gọi là tứ phân vị thứ ba hay tứ phân vị trên.
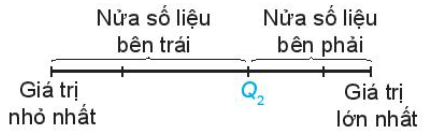
Ý nghĩa. Các điểm \(Q_{1},\ Q_{2},\
Q_{3}\) chia mẫu số liệu đã sắp xếp theo thứ tự từ nhỏ đến lớn thành bốn phần, mỗi phần đều chứa \(25\%\) giá trị (hình vẽ)
B. Bài tập minh họa tính tứ phân vị của mẫu số liệu không ghép nhóm
Ví dụ 1: Tìm tứ phân vị và mốt của các mẫu số liệu sau:
a) \(23;\ 41;\ 71;\ 29;\ 48;\ 45;\ 72;\
41\)
b) \(12;\ 32;\ 93;\ 78;\ 24;\ 12;\ 54;\
66;\ 78.\) .
Hướng dẫn giải
a) Cỡ mẫu là n = 8.
Sắp xếp các số liệu theo thứ tự không giảm ta được:
23; 29; 41; 41; 45; 48; 71; 72.
Vì cỡ mẫu là số chẵn nên tứ phân vị thứ hai là \(Q_{2} = \frac{41 + 45}{2} = 43\)
Tứ phân vị thứ nhất là trung vị của mẫu: 23; 29; 41; 41. Do đó, \(Q_{1} = \frac{29 + 41}{2} = 35\)
Tứ phân vị thứ ba là trung vị của mẫu: 45; 48; 71; 72. Do đó, \(Q_{2} = \frac{48 + 71}{2} = 59,5\)
Giá trị 41 có tần số lớn nhất (là 2), nên mốt của mẫu là Mo = 41.
b) Cỡ mẫu là n = 9.
Sắp xếp các số liệu theo thứ tự không giảm, ta được:
12; 12; 24; 32; 54; 66; 78; 78; 93.
Vì cỡ mẫu là số lẻ nên tứ phân vị thứ hai là \(Q_{2} = 54\)
Tứ phân vị thứ nhất là trung vị của mẫu: 12; 12; 24; 32. Do đó, \(Q_{1} = \frac{12 + 24}{2} = 18\)
Tứ phân vị thứ ba là trung vị của mẫu: 66; 78; 78; 93. Do đó, \(Q_{3} = \frac{78 + 78}{2} = 78\)
Các giá trị 12 và 78 đều có tần số lớn nhất nên mốt của mẫu là 12 và 78.
Ví dụ 2: Hãy tìm tứ phân vị và mốt của các mẫu số liệu sau:
a.
|
Giá trị |
23 |
25 |
28 |
31 |
33 |
37 |
|
Tần số |
6 |
8 |
10 |
6 |
4 |
3 |
b.
|
Giá trị |
0 |
2 |
4 |
5 |
|
Tần số tương đối |
0,6 |
0,2 |
0,1 |
0,1 |
Hướng dẫn giải
a) Bảng số liệu là bảng tần số. Cỡ mẫu là n = 6 + 8 + 10 + 6 + 4 + 3 = 37.
Giá trị 28 có tần số lớn nhất nên mốt của mẫu là Mo = 28.
Sắp xếp mẫu số liệu theo thứ tự không giảm, ta được:
23; 23; 23; 23; 23; 23; 25; 25; 25; 25; 25; 25;
25; 25; 28; 28; 28; 28; 28; 28; 28; 28; 28; 28;
31; 31; 31; 31; 31; 31; 33; 33; 33; 33; 37; 37; 37.
Vì cỡ mẫu là số lẻ nên tứ phân vị thứ hai là Q2 = 28.
Tứ phân vị thứ nhất là trung vị của mẫu:
23; 23; 23; 23; 23; 23; 25; 25; 25;
25; 25; 25; 25; 25; 28; 28; 28; 28.
Do đó Q1 = 25.
Tứ phân vị thứ ba là trung vị của mẫu:
28; 28; 28; 28; 28; 31; 31; 31; 31;
31; 31; 33; 33; 33; 33; 37; 37; 37.
Do đó Q3 = 31.
b) Bảng số liệu là bảng tần số tương đối.
Tần số tương đối là tỉ số của tần số với cỡ mẫu, do đó, giá trị có tần số tương đối lớn nhất thì có tần số lớn nhất, vậy giá trị 0 có tần số lớn nhất nên mốt của mẫu số liệu là Mo = 0.
Giả sử cỡ mẫu là n = 10, khi đó:
Tần số của giá trị 0 là 0,6 . 10 = 6.
Tần số của giá trị 2 là 0,2 . 10 = 2.
Tần số của giá trị 4 là 0,1 . 10 = 1.
Tần số của giá trị 5 là 0,1 . 10 = 1.
Sắp xếp các số liệu theo thứ tự không giảm, ta được:
0; 0; 0; 0; 0; 0; 2; 2; 4; 5.
Vì cỡ mẫu là số chẵn nên tứ phân vị thứ hai là Q2 = 0.
Tứ phân vị thứ nhất là trung vị của mẫu: 0; 0; 0; 0; 0. Do đó Q1 = 0.
Tứ phân vị thứ ba là trung vị của mẫu: 0; 2; 2; 4; 5. Do đó Q3 = 2.
Ví dụ 3: An lấy ra ngẫu nhiên \(3\) quả bóng từ một hộp có chứa nhiều bóng xanh và bóng đỏ. An đếm xem có bao nhiêu bóng đỏ trong \(3\) bóng lấy ra rồi trả bóng lại hộp. An lặp lại phép thử trên \(100\) lần và ghi lại kết quả ở bảng sau:
|
Số bóng đỏ |
0 |
1 |
2 |
3 |
|
Số lần |
10 |
30 |
40 |
20 |
Hãy tìm số trung bình, tứ phân vị và mốt của bảng kết quả trên.
Hướng dẫn giải
Cỡ mẫu là \(n = 100\).
Số trung bình là: \(\overline{x} = \frac{10.0 + 30.1 + 40.2
+ 20.3}{100} = 1,7\)
Số lần lấy được 2 bóng đỏ là nhiều nhất (40 lần) nên mốt của mẫu số liệu là Mo = 2.
Sắp xếp các số liệu theo thứ tự không giảm, ta được:
\(\begin{matrix}
0;\ 0;\ 0;\ 0;\ 0;\ 0;\ 0;\ 0;\ 0;\ 0;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\
1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1; \\
\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 2;\ 2;\
2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ \\
2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\
2;\ 2;\ 2;\ 2;\ 2;\ \\
2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 3;\ 3;\ 3;\ 3;\ 3;\ 3;\ 3;\ 3;\ 3;\ 3;\
3;\ 3;\ 3;\ 3;\ 3;\ 3;\ 3;\ 3;\ 3;\ 3.
\end{matrix}\)
Vì cỡ mẫu là số chẵn nên tứ phân vị thứ hai là \(Q_{2} = \frac{2 + 2}{2} = 2\).
Tứ phân vị thứ nhất là trung vị của mẫu:
\(\begin{matrix}
0;\ 0;\ 0;\ 0;\ 0;\ 0;\ 0;\ 0;\ 0;\ 0;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;
\\
\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 1; \\
\ 1;\ 1;\ 1;\ 1;\ 1;\ 1;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2.
\end{matrix}\)
Do đó \(Q_{1} = 1\)
Tứ phân vị thứ ba là trung vị của mẫu:
\(\begin{matrix}
2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ \\
2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2;\ 2; \\
\ 2;\ 2;\ 3;\ 3;\ 3;\ 3;\ 3;\ 3;\ 3;\ 3;\ 3;\ 3;\ 3;\ 3;\ 3;\ 3;\ 3;\
3;\ 3;\ 3;\ 3;\ 3.
\end{matrix}\)
Do đó \(Q_{3} = 2\)
Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!
-----------------------------------------------------------------
Như vậy, qua bài viết, bạn đã được tìm hiểu trọn vẹn về cách tính tứ phân vị trong mẫu số liệu không ghép nhóm, bao gồm định nghĩa, công thức áp dụng và ví dụ minh họa rõ ràng. Đây là nội dung quan trọng trong Toán 10, thường xuyên xuất hiện trong các đề kiểm tra, thi học kỳ cũng như đề thi tuyển sinh. Việc nắm chắc phương pháp tính tứ phân vị sẽ giúp bạn phân tích dữ liệu chính xác, xử lý tốt các dạng toán thống kê và tự tin hơn trong học tập. Hãy luyện tập thêm nhiều bài tập để củng cố kiến thức và phát triển kỹ năng phân tích số liệu.
