Xét sự đồng biến, nghịch biến của hàm số Toán 10
Xác định sự đồng biến, nghịch biến của hàm số
Việc xét sự đồng biến và nghịch biến của hàm số là kỹ năng quan trọng trong chương trình Toán 10, giúp học sinh hiểu rõ xu hướng biến thiên của hàm số và rèn luyện tư duy giải toán. Bài viết dưới đây tổng hợp lý thuyết trọng tâm, phương pháp làm bài và hệ thống bài tập Toán 10 có đáp án chi tiết, dễ hiểu.
A. Cách xét sự đồng biến, nghịch biến của hàm số
Phương pháp 1: Tìm tập xác định 
\(D\) của hàm số. Với mọi \(x_{1},x_{2} \in D\), \(x_{1} \neq x_{2}\).
- Tính \(f\left( x_{1} \right) - f\left(
x_{2} \right)\).
- Nếu \(x_{1} < x_{2} \Rightarrow f(x_{1})
< f(x_{2})\) thì hàm số đã cho đồng biến (tăng).
- Nếu \(x_{1} < x_{2} \Rightarrow f(x_{1})
> f(x_{2})\) thì hàm số đã cho nghịch biến (giảm).
Phương pháp 2: Tìm tập xác định \(D\) của hàm số.
- Với mọi \(x_{1},x_{2} \in D\), \(x_{1} \neq x_{2}\). Lập tỉ số \(\frac{f\left( x_{1} \right) - f\left( x_{2}
\right)}{x_{1} - x_{2}}\).
- Nếu \(\frac{f\left( x_{1} \right) - f\left(
x_{2} \right)}{x_{1} - x_{2}} > 0\) thì hàm số đã cho đồng biến (tăng).
- Nếu \(\frac{f\left( x_{1} \right) - f\left(
x_{2} \right)}{x_{1} - x_{2}} < 0\) thì hàm số đã cho nghịch biến (giảm).
B. Bài tập minh họa về sự đồng biến nghịch biến của hàm số
Ví dụ 1: Cho hàm số \(f(x) = x +
1.\)
a) So sánh \(f(1)\) và \(f(2)\).
b) Chứng minh rằng nếu \(x_{1};x_{2}\mathbb{\in R}\) sao cho \(x_{1} < x_{2}\) thì \(f\left( x_{1} \right) < f\left( x_{2}
\right)\).
Hướng dẫn giải
a) Ta có: \(f(x) = x + 1\)
Khi đó: \(\left\{ \begin{matrix}
f(1) = 1 + 1 = 2 \\
f(2) = 2 + 1 = 3
\end{matrix} \right.\)
Vì \(2 < 3\) nên \(f(1) < f(2)\). Vậy \(f(1) < f(2)\).
b) Ta có: \(f\left( x_{1} \right) =
x_{1}\ + 1;f\left( x_{2} \right) = x_{2}\ + 1\)
Vì \(x_{1} < x_{2}\) nên \(x_{1} + 1 < x_{2} + 1\) (liên hệ giữa thứ tự và phép cộng)
Do đó: \(f\left( x_{1} \right) < f\left(
x_{2} \right)\) với mọi \(x_{1};x_{2}\mathbb{\in R}\)
Ví dụ 2: Cho hàm số \(y = f(x)\) có đồ thị như hình vẽ:
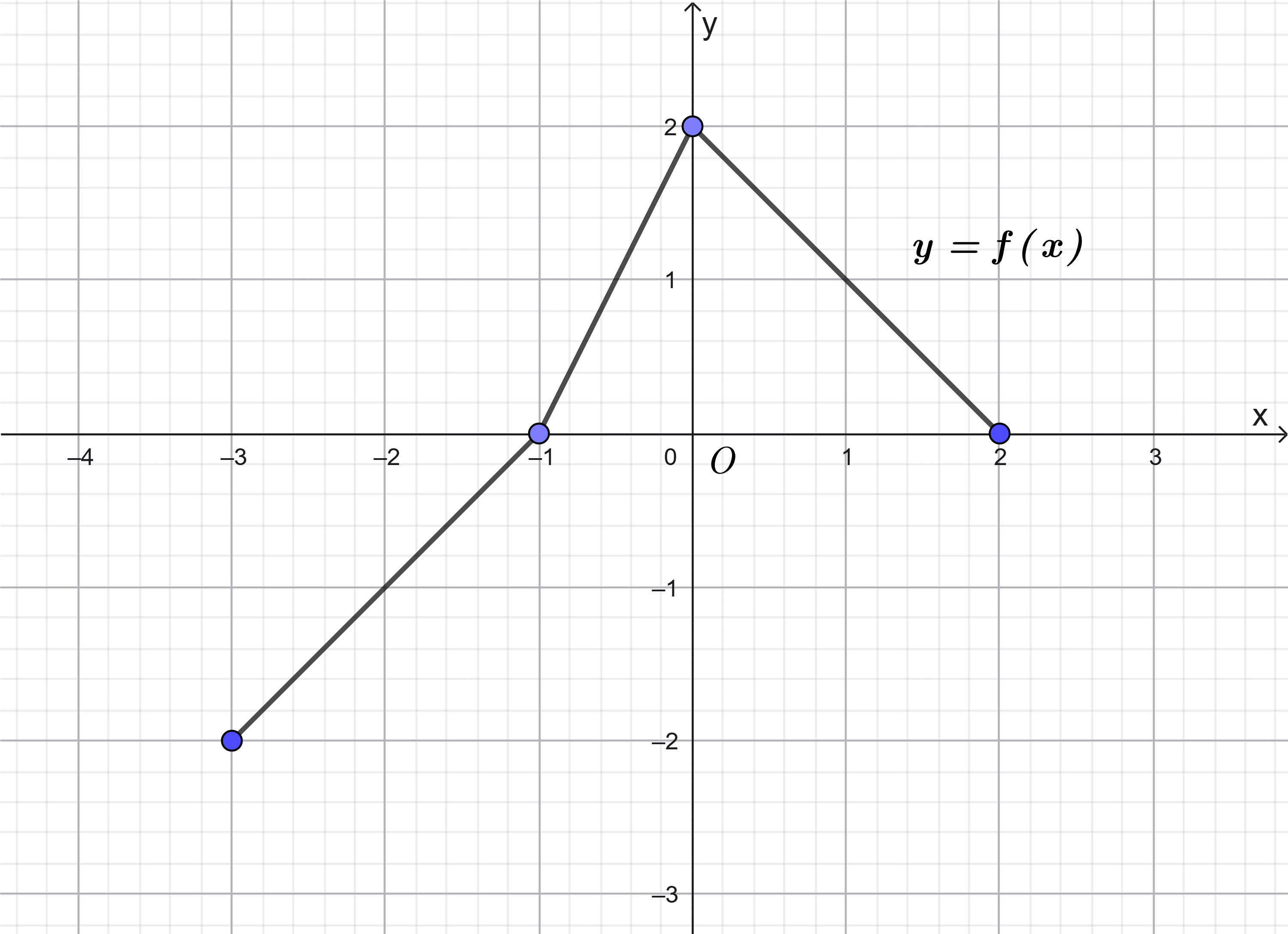
Chỉ ra khoảng đồng biến và khoảng nghịch biến của hàm số \(y = f(x)\).
Hướng dẫn giải
Quan sát đồ thị hàm số y = f(x) ở hình vẽ, ta thấy:
+ Đồ thị hàm số “đi lên” (theo chiều từ trái qua phải) trong các khoảng (– 3; – 1) và (– 1; 0) nên hàm số đã cho đồng biến trên các khoảng (– 3; –1) và (–1; 0).
+ Đồ thị hàm số “đi xuống” (theo chiều từ trái qua phải) trong khoảng (0; 2) nên hàm số đã cho nghịch biến trên khoảng (0; 2).
Ví dụ 3: Vẽ đồ thị hàm số \(y = |x -
1|.\) Từ đồ thị, hãy tìm khoảng đồng biến, khoảng nghịch biến và tập giá trị của hàm số.
Hướng dẫn giải
Ta có: \(y = |x - 1| = \left\{
\begin{matrix}
x - 1\ \ \ khi\ \ \ x \geq 1 \\
1 - x\ \ \ khi\ \ \ x < 1
\end{matrix} \right.\)
Với \(x \geq 1\)thì đồ thị hàm số \(y = x - 1\) là đường thẳng đi qua hai điểm (1;0), (2;1) và nằm bên phải đường thẳng x = 1.
Với \(x < 1\) thì đồ thị hàm số \(y = 1 - x\) là đường thẳng đi qua hai điểm (0;1), (-1;2) và nằm bên trái đường thẳng x = 1.
Đồ thị hàm số \(y = |x - 1|\) như hình dưới đây:
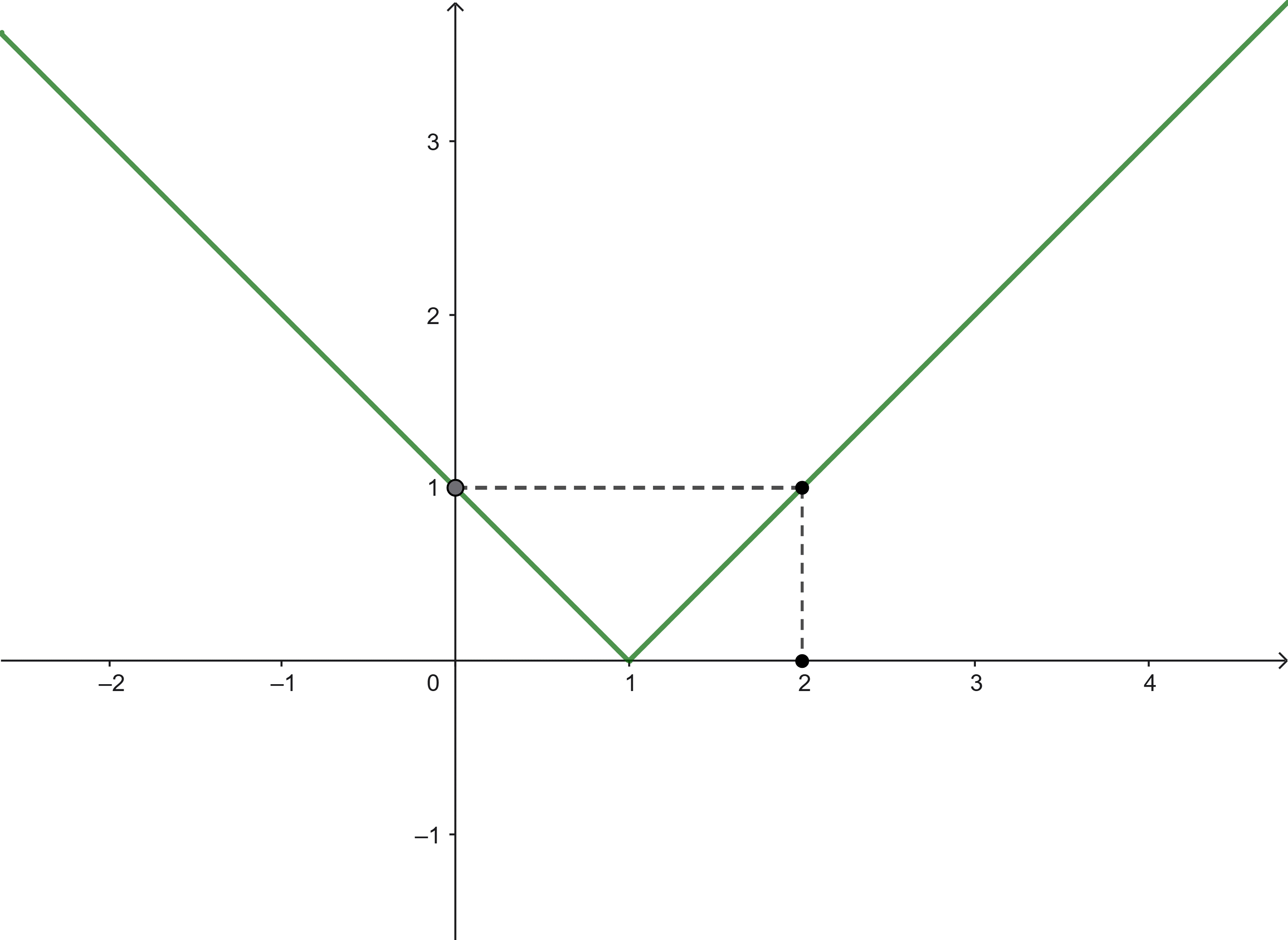
Từ đồ thị ta suy ra:
Hàm số đồng biến trên khoảng \((1; +
\infty)\\); nghịch biến trên khoảng \(\ \ ( - \infty;1)\)
Tập giá trị của hàm số là \(\lbrack 0; +
\infty)\\)
C. Bài tập vận dụng có hướng dẫn chi tiết
Bài tập 1. Cho hàm số \(y = f(x)\) có đồ thị hình vẽ dưới đây:
Quan sát đồ thị, hãy hãy cho biết phát biểu nào đúng
a) Hàm số \(y = f(x)\) đồng biến trên khoảng \(( - 2; - 1)\\)
b) Hàm số \(y = f(x)\) đồng biến trên khoảng \(( - 2;2)\\)
c) Hàm số \(y = f(x)\) nghịch biến trên khoảng \((0; + \infty)\\).
Bài tập 2. Xét tính đồng biến và nghịch biến của hàm số \(f(x) = x^{2} - 7\) trên khoảng \(( - \infty;0)\) và trên khoảng \((0; + \infty)\).
Bài tập 3: Xét tính đồng biến và nghịch biến của hàm số \(f(x) = \frac{x}{x - 1}\) trên khoảng \(( - \infty;1)\) và trên khoảng \((1; + \infty)\).
Không thể hiển thị hết nội dung tại đây — bấm Tải về để lấy toàn bộ tài liệu.
-------------------------------------
Hy vọng với lý thuyết, phương pháp và các bài tập kèm đáp án, bạn đã nắm vững cách xét hàm số đồng biến – nghịch biến trong Toán 10. Hãy luyện tập thêm để tăng tốc độ và độ chính xác khi giải các bài liên quan.
