Cách dùng kí hiệu Đoạn, Khoảng, Nửa khoảng để viết các tập hợp Toán lớp 10
Cách viết tập hợp bằng đoạn khoảng trong Toán 10
Trong chuyên đề Tập hợp Toán 10, một nội dung quan trọng là cách sử dụng kí hiệu Đoạn, Khoảng và Nửa khoảng để biểu diễn các tập hợp số. Việc nắm chắc kiến thức này không chỉ giúp học sinh viết tập hợp một cách ngắn gọn, chính xác mà còn rèn luyện tư duy toán học logic, phục vụ tốt cho các bài tập giải phương trình, bất phương trình và nhiều ứng dụng khác.
Bài viết sẽ hướng dẫn chi tiết cách dùng kí hiệu Đoạn, Khoảng, Nửa khoảng để viết các tập hợp Toán lớp 10, kèm theo bài tập minh họa và đáp án chi tiết. Qua đó, học sinh dễ dàng hiểu bản chất, áp dụng thành thạo và đạt kết quả cao trong học tập.
A. Các tập hợp số đã học
- Tập hợp số tự nhiên
\(\mathbb{N =}\{
0;1;2;3;\ldots\}\). - Tập hợp số nguyên \(\mathbb{Z =}\{\ldots; -
3; - 2; - 1;0;1;2;3;\ldots\}\).
- Tập hợp số hữu tỉ \(\mathbb{Q}\) gồm các số viết được dưới dạng \(\frac{m}{n}\), với \(m,n\mathbb{\in Z}\) và \(n \neq 0\).
- Tập hợp số thực \(\mathbb{R}\) gổm các số hữu tỉ và các số vô tỉ.
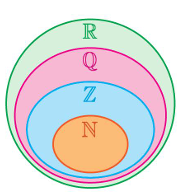
Mối quan hệ giữa các tập hợp này là: \(\mathbb{N \subset Z \subset Q \subset R}\) (tham khảo hình vẽ)
B. Biểu diễn một số tập hợp thường gặp trên trục số
Chú ý:
+) Kí hiệu \(+ \infty\) đọc là "dương vô cực" hoặc "dương vô cùng"; kí hiệu \(- \infty\) đọc là "âm vô cực" hoặc "âm vô cùng".
+) \(a\) và \(b\) gọi là hai đẩu mút của đoạn, khoảng, nửa khoảng.
B. Bài tập ví dụ minh họa cách viết và biểu diễn tập hợp
Ví dụ 1: Dùng kí hiệu đoạn, khoảng, nửa khoảng để viết các tập hợp sau và biểu diễn các tập hợp đó trên trục số:
a) \(A = \{ x\mathbb{\in R} \mid - 2 \leq x
< 5\}\); b) \(B = \{ x\mathbb{\in R}
\mid x > \sqrt{2}\}\); c) \(C = \{
x\mathbb{\in R} \mid 1 - x \geq 0\}\).
Hướng dẫn giải
a) \(A = \{ x\mathbb{\in R} \mid - 2 \leq x
< 5\} = \lbrack - 2;5)\).
Biểu diễn trên trục số:
b) \(B = \{ x\mathbb{\in R} \mid x >
\sqrt{2}\} = \left( \sqrt{2}; + \infty \right)\).
Biểu diễn trên trục số:
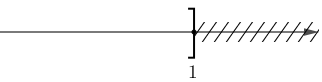
c) Ta có \(1 - x \geq 0 \Leftrightarrow x
\leq 1\). Do đó \(C = \{ x\mathbb{\in
R} \mid 1 - x \geq 0\} = ( - \infty;1\rbrack\).
Biểu diễn trên trục số:
Ví dụ 2: Dùng kí hiệu đoạn, khoảng, nửa khoảng để viết các tập hợp sau và biểu diễn các tập hợp đó trên trục số:
a) \(A = \{ x\mathbb{\in R} \mid 0 < x
\leq 3\}\); b) \(B = \{ x\mathbb{\in R}
\mid x \leq - 2\}\);
c) \(C = \{ x\mathbb{\in R} \mid 1 - 2x
< 0\}\); d) \(A = \{ x\mathbb{\in R}
\mid 1 \leq x \leq 4\}\).
Hướng dẫn giải
a) \(A = \{ x\mathbb{\in R} \mid 0 < x
\leq 3\} = (0;3\rbrack\).
Biểu diễn trên trục số:
b) \(B = \{ x\mathbb{\in R} \mid x \leq -
2\} = ( - \infty; - 2\rbrack\).
Biểu diễn trên trục số:
c) Ta có \(1 - 2x < 0 \Leftrightarrow x
> \frac{1}{2}\).
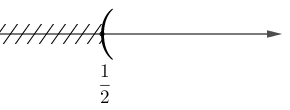
Do đó \(C = \{
x\mathbb{\in R} \mid 1 - 2x < 0\} = \left( \frac{1}{2}; + \infty
\right)\).
Biểu diễn trên trục số:
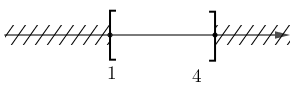
d) \(A = \{ x\mathbb{\in R} \mid 1 \leq x
\leq 4\} = \lbrack 1;4\rbrack\).
Biểu diễn trên trục số:
C. Bài tập tự rèn luyện có đáp án chi tiết
Bài tập 1: Dùng ki hiệu \(\subset\) để mô tả quan hệ của hai tập hợp khác nhau trong các tập hợp sau: \(( - 1;3);\lbrack - 1;3);\lbrack -
1;3\rbrack\).
Bài tập 2: Dùng ki hiệu \(\subset\) để mô tả quan hệ của ba tập hợp khác nhau trong các tập hợp sau: \(( - 1;3);( - 1;3\rbrack;\lbrack - 1;3);\lbrack -
1;3\rbrack\).
Bài tập 3: Cho tập hợp \(A = \lbrack
2;5)\) và tập hợp \(B = (m;m +
8)\). Có bao nhiêu giá trị nguyên của \(m\) để \(A\) là tập con của \(B\)?
Bài tập 4: Cho hai tập hợp \(A = \lbrack
1;5)\) và \(B = \lbrack m;m + 1\rbrack\). Có bao nhiêu giá trị nguyên của \(m\) để \(B\) là tập con của \(A\)?
Bạn muốn xem toàn bộ tài liệu? Hãy nhấn Tải về ngay!
---------------------------------------------------------
Việc thành thạo cách dùng kí hiệu Đoạn, Khoảng, Nửa khoảng để viết các tập hợp là nền tảng quan trọng để học sinh giải quyết tốt các dạng toán về bất phương trình, hàm số và biểu diễn tập hợp trên trục số. Khi nắm vững kiến thức này, học sinh sẽ tự tin hơn trong quá trình làm bài, đồng thời hạn chế tối đa sai sót trong biểu diễn kết quả.
Để học hiệu quả, ngoài việc ghi nhớ định nghĩa, học sinh cần luyện tập nhiều bài tập biểu diễn tập hợp bằng kí hiệu khoảng – đoạn – nửa khoảng kèm đáp án. Đây là phương pháp học tập khoa học, giúp củng cố kiến thức nhanh chóng và áp dụng dễ dàng vào các dạng bài nâng cao trong Toán 10 và các lớp sau.
