Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12 Toán 12 Chuyên đề Toán 12
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Bài tập Toán 12: Bài toán tương giao với hàm hợp, hàm ẩn

Ôn thi THPT Quốc Gia môn Toán

VnDoc.com xin gửi tới bạn đọc bài viết Trắc nghiệm Toán 12: Bài tập toán 12 Tương giao đồ thị hàm ẩn. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây nhé!

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 22 câu
  • Điểm số bài kiểm tra: 22 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Vận dụng cao
    Chọn đáp án đúng

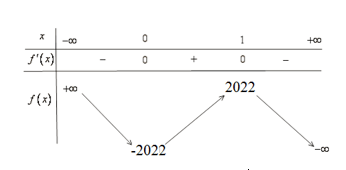
    Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên.

    Số nghiệm thực của phương trình \left| f\left( x^{4} - 2x^{2} \right) \right| = 2 là

    Hướng dẫn:

    Phương trình \left| f\left( x^{4} - 2x^{2} ight) ight| = 2 \Leftrightarrow \left\lbrack \begin{matrix} f\left( x^{4} - 2x^{2} ight) = 2 \\ f\left( x^{4} - 2x^{2} ight) = - 2 \\ \end{matrix}. ight.

    * Phương trình f\left( x^{4} - 2x^{2} ight) = 2

    \Leftrightarrow \left\lbrack \begin{matrix} x^{4} - 2x^{2} = b,( - 1 < b < 0) \\ \begin{matrix} x^{4} - 2x^{2} = c,(0 < c < 1) \\ x^{4} - 2x^{2} = d,(2 < d < 3) \\ \end{matrix} \\ \end{matrix} ight..

    * Phương trình f\left( x^{4} - 2x^{2} ight) = - 2 \Leftrightarrow x^{4} - 2x^{2} = a,( - 2 < a < - 1).

    Đồ thị hàm số y = x^{4} - 2x^{2} như hình vẽ sau:

    Dựa vào đồ thị trên ta có:

    - Phương trình x^{4} - 2x^{2} = a,( - 2 < a < - 1) không có nghiệm thực.

    - Phương trình x^{4} - 2x^{2} = b,( - 1 < b < 0) có 4 nghiệm thực phân biệt.

    - Phương trình x^{4} - 2x^{2} = c,(0 < c < 1) có 2 nghiệm thực phân biệt.

    - Phương trình x^{4} - 2x^{2} = d,(2 < d < 3) có 2 nghiệm thực phân biệt.

    Vậy phương trình \left| f\left( x^{4} - 2x^{2} ight) ight| = 2 có 8 nghiệm thực phân biệt.

    Nhận xét: Khi bài toán chứa dấu giá trị tuyệt đối ta đi phá dấu giá trị tuyệt đối bằng phép biến đổi tương đương \left| f(x) ight| = A \Leftrightarrow \left\lbrack \begin{matrix} f(x) = A \\ f(x) = - A \\ \end{matrix} ight. .

  • Câu 2: Vận dụng cao
    Tìm các giá trị nguyên m thỏa mãn yêu cầu

    Cho hàm y = f(x) là hàm đa thức bậc bốn. Biết rằng f(0) = 0, f( - 3) = f\left( \frac{3}{2} \right) = - \frac{19}{4} và đồ thị hàm số y = f'(x) có dạng như hình vẽ.

    Xét hàm số g(x) = \left| 4f(x) + 2x^{2} \right| - 2m^{2} + 1 với m là tham số thực. Có tất cả bao nhiêu giá trị nguyên m \in ( - 50;50) để phương trình g(x) = 1 có đúng hai nghiệm thực?

    Hướng dẫn:

    Ta có \left| 4f(x) + 2x^{2} ight| - 2m^{2} + 1 = 1

    \Leftrightarrow \left| 4f(x) + 2x^{2} ight| = 2m^{2}(1)

    Xét hàm số h(x) = 4f(x) + 2x^{2}, ta có h'(x) = 4\left\lbrack f'(x) - ( - x) ightbrack.

    Dựa vào đồ thị hàm số f'(x) và đường thẳng y = - x.

    Ta thấy: h'(x) = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = - 3 \\ x = 0 \\ x = \frac{3}{2} \\ \end{matrix} ight.

    và h( - 3) = 4f( - 3) + 2( - 3)^{2} = - 1, h(0) = 0, h\left( \frac{3}{2} ight) = 4f\left( \frac{3}{2} ight) + 2\left( \frac{3}{2} ight)^{2} = - \frac{29}{2}.

    Do đó ta có bảng biến thiên hàm số h(x) như sau

    Từ đó suy ra bảng biến thiên của hàm số \left| h(x) ight|như sau

    Do đó để phương trình (1)có đúng hai nghiệm thực thì 2m^{2} > \frac{29}{2} \Leftrightarrow \left\lbrack \begin{matrix} m > \frac{\sqrt{29}}{2} \\ m < - \frac{\sqrt{29}}{2} \\ \end{matrix} ight..

    Mà m là số nguyên thuộc ( - 50;50) nên \left\lbrack \begin{matrix} 3 \leq m \leq 49 \\ - 49 \leq m \leq - 3 \\ \end{matrix} ight..

    Vậy có 94 số nguyên m thỏa mãn.

  • Câu 3: Vận dụng cao
    Chọn đáp án chính xác

    Cho hàm số f(x) liên tục trên \lbrack 2;4brack và có bảng biến thiên như hình vẽ bên. Có bao nhiêu giá trị nguyên của m để phương trình x + 2\sqrt{x^{2} - 2x} = m.f(x) có nghiệm thuộc đoạn \lbrack 2;4brack?

    Hướng dẫn:

    Dựa vào bảng biến thiên ta có\underset{\lbrack 2;4brack}{Min}f(x) = f(4) = 2 và \underset{\lbrack 2;4brack}{Max}f(x) = f(2) = 4

    Hàm số g(x) = x + 2\sqrt{x^{2} - 2x} liên tục và đồng biến trên \lbrack 2;4brack

    Suy ra \underset{\lbrack 2;4brack}{Min}g(x) = g(2) = 2 và \underset{\lbrack 2;4brack}{Max}g(x) = g(4) = 4 + 4\sqrt{2}

    Ta có x + 2\sqrt{x^{2} - 2x} = m.f(x) \Leftrightarrow \frac{x + 2\sqrt{x^{2} - 2x}}{f(x)} = m \Leftrightarrow \frac{g(x)}{f(x)} = m

    Xét hàm số h(x) = \frac{g(x)}{f(x)} liên tục trên \lbrack 2;4brack

    Vì g(x) nhỏ nhất và f(x) lớn nhất đồng thời xảy ra tại x = 2 nên \underset{\lbrack 2;4brack}{Min}h(x) = \frac{\underset{\lbrack 2;4brack}{Min}g(x)}{\underset{\lbrack 2;4brack}{Max}f(x)} = \frac{g(2)}{f(2)} = h(2) = \frac{1}{2}

    Vì g(x) lớn nhất và f(x) nhỏ nhất đồng thời xảy ra tại x = 4 nên \underset{\lbrack 2;4brack}{Max}h(x) = \frac{\underset{\lbrack 2;4brack}{Max}g(x)}{\underset{\lbrack 2;4brack}{Min}f(x)} = \frac{g(4)}{f(4)} = h(4) = 2 + 2\sqrt{2}

    Từ đó suy ra phương trình h(x) = m có nghiệm khi và chỉ khi \frac{1}{2} \leq m \leq 2 + 2\sqrt{2}.

    Vậy có 4 giá trị nguyên của m để phương trình có nghiệm.

  • Câu 4: Vận dụng cao
    Tính giá trị biểu thức

    Gọi m_{0} là số thực sao cho phương trình \left| x^{3} - 12x \right| = m_{0} có ba nghiệm dương phân biệt x_{1}; x_{2}; x_{3} thỏa mãn x_{1} + x_{2} + x_{3} = 1 + 4\sqrt{3}. Biết rằng m_{0} có dạng a\sqrt{3} + b với a; b là các số hữu tỷ. Tính 4a^{2} + 8b:

    Hướng dẫn:

    Vẽ đồ thị hàm số y = \left| x^{3} - 12x ight|

    Do đó với mọi m \in (0\ ;\ 16) thì phương trình đã cho luôn có ba nghiệm dương phân biệt x_{1}; x_{2}; x_{3} \left( x_{1} < x_{2} < x_{3} ight) thỏa mãn: \left\{ \begin{matrix} - x_{1}^{3} + 12x_{1} = m_{0} \\ - x_{2}^{3} + 12x_{2} = m_{0} \\ x_{3}^{3} - 12x_{3} = m_{0} \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} \left( - x_{1} ight)^{3} - 12\left( - x_{1} ight) - m_{0} = 0 \\ \left( - x_{2} ight)^{3} - 12\left( - x_{2} ight) - m_{0} = 0 \\ x_{3}^{3} - 12x_{3} - m_{0} = 0 \\ \end{matrix} ight.

    \Rightarrow - x_{1}; - x_{2}; x_{3} là ba nghiệm của phương trình x^{3} - 12x - m_{0} = 0

    \Rightarrow - x_{1} - x_{2} + x_{3} = 0 \Rightarrow x_{3} = x_{1} + x_{2}

    Mà x_{1} + x_{2} + x_{3} = 1 + 4\sqrt{3} \Rightarrow x_{3} = \frac{1 + 4\sqrt{3}}{2}

    \Rightarrow m_{0} = \left( \frac{1 + 4\sqrt{3}}{2} ight)^{3} - 12\left( \frac{1 + 4\sqrt{3}}{2} ight) = \frac{3\sqrt{3}}{2} + \frac{97}{8}

    \Rightarrow a = \frac{3}{2}; b = \frac{97}{8} \Rightarrow 4a^{2} + 8b = 106.

  • Câu 5: Vận dụng cao
    Định m để bất phương trình nghiệm đúng với mọi x

    Cho hàm số f(x). Hàm số y = f'(x) có đồ thị như hình sau.

    Tìm tất cả các giá trị thực của tham số m để bất phương trình 2f\left( \sin x - 2 \right) - \frac{2sin^{3}x}{3} + \sin x > m + \frac{5cos2x}{4} nghiệm đúng với mọi x \in \left( - \frac{\pi}{2};\frac{\pi}{2} \right).

    Hướng dẫn:

    Ta có

    2f\left( \sin x - 2 ight) - \frac{2sin^{3}x}{3} + \sin x > m + \frac{5cos2x}{4}

    \Leftrightarrow m < 2f\left( \sin x - 2 ight) - \frac{2sin^{3}x}{3} + \sin x - \frac{5\left( 1 - 2sin^{2}x ight)}{4}

    Đặt t = \sin x - 2 (với x \in \left( - \frac{\pi}{2};\frac{\pi}{2} ight) thì t \in ( - 3; - 1)

    Khi đó bất phương trình được viết lại thành:

    m < 2f(t) - \frac{2(t + 2)^{3}}{3} + (t + 2) - \frac{5\left\lbrack 1 - 2(t + 2)^{2} ightbrack}{4}.

    Hay m < 2f(t) - \frac{2}{3}t^{3} - \frac{3}{2}t^{2} + 3t + \frac{65}{12}(*).

    Xét hàm số g(t) = 2f(t) - \frac{2}{3}t^{3} - \frac{3}{2}t^{2} + 3t + \frac{65}{12} trên đoạn \lbrack - 3; - 1brack.

    Ta có g'(t) = 2f'(t) - 2t^{2} - 3t + 3.

    Do đó g'(t) = 0 \Leftrightarrow f'(t) = t^{2} + \frac{3}{2}t - \frac{3}{2}.

    Dựa vào sự tương giao của đồ thị hàm số y = f'(t) và parabol y = t^{2} + \frac{3}{2}t - \frac{3}{2} trên đoạn \lbrack - 3; - 1brack thì g'(t) = 0 \Leftrightarrow t \in \left\{ - 3; - 1 ight\}.

    Suy ra bảng biến thiên của hàm số g(t) trên đoạn \lbrack - 3; - 1brack như sau:

    Bất phương trình đã cho nghiệm đúng với mọi x \in \left( - \frac{\pi}{2};\frac{\pi}{2} ight) khi và chỉ khi bất phương trình (*) nghiệm đúng với mọi t \in ( - 3; - 1). Điều đó tương đương với m \leq g( - 1) = 2f( - 1) + \frac{19}{12} dựa vào tính liên tục của hàm số g(t).

  • Câu 6: Vận dụng cao
    Tìm m để phương trình có 3 nghiệm thực phân biệt

    Cho hàm số y = f(x) có bảng biến thiên như hình vẽ:

    Có bao nhiêu giá trị nguyên của tham số m để phương trình 6f\left( x^{2} - 4x \right) = m có ít nhất ba nghiệm thực phân biệt thuộc khoảng (0\ ;\ + \infty)?

    Hướng dẫn:

    Ta đặt: g(x) = f\left( x^{2} - 4x ight).

    g'(x) = (2x - 4)f'\left( x^{2} - 4x ight)

    = 2(x - 2)\left( x^{2} - 4x + 4 ight)\left( x^{2} - 4x + 2 ight)\left( x^{2} - 4x ight) (dựa vào bảng biến thiên) = 2(x - 2)^{3}\left( x^{2} - 4x + 2 ight)x(x - 4).

    Mặt khác:

    g(0) = f(0) = - 3;

    g\left( 2 - \sqrt{2} ight) = g\left( 2 + \sqrt{2} ight) = f( - 2) = 2;

    g(2) = f( - 4) = - 2;

    g(4) = f(0) = - 3.

    Ta có bảng biến thiên:

    Từ bảng biến thiên ta được: yêu cầu bài toán tương đương - 3 < \frac{m}{6} \leq 2

    \Leftrightarrow - 18 < m \leq 12. Vậy có tất cả 30 giá trị của tham số m thỏa mãn yêu cầu bài toán.

  • Câu 7: Thông hiểu
    Chọn dáp án đúng

    Cho hàm số y = f(x) liên tục trên \mathbb{R} thỏa mãn f( - 1) = 5,f( - 3) = 0 và có bảng xét dấu đạo hàm như sau:

    Số giá trị nguyên dương của tham số m để phương trình 3f(2 - x) + \sqrt{x^{2} + 4} - x = m có nghiệm trong khoảng (3;5) là

    Hướng dẫn:

    Đặt g(x) = 3f(2 - x) + \sqrt{x^{2} + 4} - x với x \in (3;5).

    Ta có: g'(x) = - 3f'(2 - x) + \frac{x}{\sqrt{x^{2} + 4}} - 1.

    Với x \in (3;5):

    Ta có: 2 - x \in ( - 3; - 1) nên f'(2 - x) > 0 suy ra - 3f'(2 - x) < 0.

    Ta có: \frac{x}{\sqrt{x^{2} + 4}} < \frac{x}{x} = 1

    Suy ra g'(x) = - 3f'(2 - x) + \frac{x}{\sqrt{x^{2} + 4}} - 1 < 0,\forall x \in (3;5) nên hàm số nghịch biến trên (3;5).

    Suy ra \min_{(3;5)}g(x) = g(5) = 3f( - 3) + \sqrt{5^{2} + 4} - 5 = \sqrt{29} - 5;

    \max_{(3;5)}g(x) = g(3) = 3f( - 1) + \sqrt{3^{2} + 4} - 3 = 12 + \sqrt{13}.

    Để phương trình 3f(2 - x) + \sqrt{x^{2} + 4} - x = m có nghiệm thì \sqrt{29} - 5 \leq m \leq 12 + \sqrt{13} mà m nguyên dương nên m \in \left\{ 1,2,...,15 ight\} tức là có 15 giá trị.

  • Câu 8: Vận dụng cao
    Tìm m để phương trình có 3 nghiệm thực phân biệt

    Cho hàm số f(x) = log_{3}x + 3^{x} - 3^{\frac{1}{x}}. Tổng bình phương các giá trị của tham số m để phương trình f\left( \frac{1}{4|x - m| + 3} \right) + f\left( x^{2} - 4x + 7 \right) = 0 có đúng 3 nghiệm thực phân biệt bằng

    Hướng dẫn:

    Ta có f'(x) = \frac{1}{xln3} + 3^{x} \cdot ln3 + \frac{1}{x^{2}} \cdot 3^{\frac{1}{x}} \cdot ln3 > 0,\forall x > 0

    \Rightarrow Hàm số y = f(x) đồng biến trên (0; + \infty)(1).

    Mặt khác f\left( \frac{1}{x} ight) = log_{3}\frac{1}{x} + 3^{\frac{1}{x}} - 3^{x} = - \left( log_{3}x - 3^{\frac{1}{x}} + 3^{x} ight) = - f(x), khi đó

    f\left( \frac{1}{4|x - m| + 3} ight) + f\left( x^{2} - 4x + 7 ight) = 0

    \Leftrightarrow - f(4|x - m| + 3) + f\left( x^{2} - 4x + 7 ight) = 0

    \Leftrightarrow f\left( 4|x - m| + 3 ight) = f\left( x^{2} - 4x + 7 ight)\ \ (2).

    Từ (1),(2) \Rightarrow 4|x - m| + 3 = x^{2} - 4x + 7

    \Leftrightarrow \left\lbrack \begin{matrix} 4m = - x^{2} + 8x - 4 \\ 4m = x^{2} + 4 \\ \end{matrix} ight..

    Ta có đồ thị sau:

    Theo yêu cầu bài toán tương đương \left\lbrack \begin{matrix} 4m = 4 \\ 4m = 8 \\ 4m = 12 \\ \end{matrix} \Leftrightarrow \left\lbrack \begin{matrix} m = 1 \\ m = 2 \\ m = 3 \\ \end{matrix} ight.\ ight.. Vậy 1^{2} + 2^{2} + 3^{2} = 14.

  • Câu 9: Vận dụng cao
    Tìm số nghiệm thực phân biệt của phương trình

     Cho hàm số bậc bay = f(x)có đồ thị là đường cong trong hình vẽ bên. Số nghiệm thực phân biệt của phương trình f\left( \left| \sqrt{4 - x^{2}} - \left| x^{2} - 1 \right| \right| \right) = \frac{1}{2023} là

    Hướng dẫn:

    Ta có:

    y = g(x) = f\left( \left| \sqrt{4 - x^{2}} - \left| x^{2} - 1 ight| ight| ight) với g(x) = \frac{1}{2023}

    Ta đặt: t = \sqrt{4 - x^{2}},\forall x \in \lbrack - 2;2brack thì suy ra y = g(t) = f\left( \left| t - \left| t^{2} - 3 ight| ight| ight),\forall t \in \lbrack 0;2brack

    Suy ra: h(t) = t - \left| t^{2} - 3 ight| = \left\{ \begin{matrix} t^{2} + t - 3,t \in \left\lbrack 0;\sqrt{3} ightbrack \\ - t^{2} + t + 3,t \in \left\lbrack \sqrt{3};2 ightbrack \\ \end{matrix} ight..

    Từ đó ta có BBT của hàm số h(t) như hình vẽ bên:

    Đặt u = \left| t - \left| t^{2} - 3 ight| ight|thì ta cũng có BBT của unhư sau:

    Nhìn vào đồ thị y = f(x)trên ta có được:

     

    Như vậy ta suy ra f(x) = \frac{2}{3}x(x - 1)(x - 2).

    Mà hàm số đó có cực trị bằng - \frac{4\sqrt{3}}{9} tại x = x_{0}

    Suy ra f\left( x_{0} ight) = \frac{- 4\sqrt{3}}{9} \Rightarrow x_{0} = \frac{3 + \sqrt{3}}{3}

    Như vậy: f(3) = 4,f\left( \sqrt{3} ight) = - 0,2,f\left( \frac{3 + \sqrt{3}}{3} ight) = \frac{- 4\sqrt{3}}{9}

    Từ đó, ta phác họa được đồ thị y = f(u) với u = \left| t - \left| t^{2} - 3 ight| ight| như sau:

    Dựa vào hình vẽ trên, ta kết luận phương trình g(x) = \frac{1}{2023}có tất cả 10 nghiệm phân biệt

  • Câu 10: Vận dụng cao
    Tính giá trị biểu thức

    Trong số các cặp số thực (a;b) để bất phương trình (x - 1)(x - a)\left( x^{2} + x + b \right) \geq 0 nghiệm đúng với mọi x\mathbb{\in R}, tích ab nhỏ nhất bằng

    Hướng dẫn:

    Đặt f(x) = (x - 1)(x - a)\left( x^{2} + x + b ight) và g(x) = (x - a)\left( x^{2} + x + b ight)

    Giả sử x = 1 không phải là nghiệm của phương trình g(x) = (x - a)\left( x^{2} + x + b ight) = 0 thì hàm số f(x) = (x - 1)(x - a)\left( x^{2} + x + b ight) sẽ đổi dấu khi qua điểm x = 1, nghĩa là(x - 1)(x - a)\left( x^{2} + x + b ight) \geq 0 không nghiệm đúng với mọi x\mathbb{\in R}.

    Do đó yêu cầu bài toán được thỏa mãn thì một điều kiện cần làg(x) = (x - a)\left( x^{2} + x + b ight) = 0 có nghiệm x = 1 suy ra hoặc \left\{ \begin{matrix} a = 1 \\ x^{2} + x + b \geq 0,\ \forall x\mathbb{\in R} \\ \end{matrix} ight. hoặc là phương trình x^{2} + x + b = 0 có hai nghiệm x = 1 và x = a

    Trường hợp 1: \left\{ \begin{matrix} a = 1 \\ x^{2} + x + b \geq 0,\forall x \in R \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} a = 1 \\ 1 > 0 \\ \Delta = 1 - 4b \leq 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} a = 1 \\ b \geq \frac{1}{4} \\ \end{matrix} ight.

    Trường hợp 2: phương trình x^{2} + x + b = 0 có hai nghiệm x = 1 và x = a

    Ta thay x = 1vào phương trình x^{2} + x + b = 0 có 1^{2} + 1 + b = 0 \Rightarrow b = - 2.

    Với b = - 2 có phương trình x^{2} + x + b = 0 \Leftrightarrow x^{2} + x - 2 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = - 2 \\ \end{matrix} ight.

    Vì x = a cũng là nghiệm của phương trình nên a = - 2.

    Trong trường hợp 1: \left\{ \begin{matrix} a = 1 \\ b \geq \frac{1}{4} \\ \end{matrix} ight.\ \Rightarrow ab \geq \frac{1}{4} suy ra tích ab nhỏ nhất khi ab = \frac{1}{4}

    Và với a = 1,b = \frac{1}{4}, tích ab = \frac{1}{4} thì bất phương trình đã cho tương đương với (x - 1)(x - 1)\left( x^{2} + x + \frac{1}{4} ight) \geq 0 \Leftrightarrow (x - 1)^{2}\left( x + \frac{1}{2} ight)^{2} \geq 0 thỏa mãn với mọi x\mathbb{\in R} (nhận)

    Trong trường hợp 2: Tích ab = 4 > \frac{1}{4}

    Vậy tích ab nhỏ nhất khi ab = \frac{1}{4}.

  • Câu 11: Vận dụng cao
    Chọn đáp án chính xác

    Cho hàm số f(x) liên tục trên \mathbb{R} và có đồ thị như hình vẽ.

    Có bao nhiêu giá trị nguyên của tham số m để phương trình f\left( \left| \frac{3sinx - \cos x - 1}{2cosx - \sin x + 4} \right| + 2 \right) = f\left( \sqrt{(m + 2)^{2} + 4} \right) có nghiệm?

    Hướng dẫn:

    Ta có: - 1 \leq \sin x \leq 1,\ \ - 1 \leq \cos x \leq 1 nên suy ra 2cosx - \sin x + 4 > 0,\ \ \forall x\mathbb{\in R}.

    Đặt t = \frac{3sinx - \cos x - 1}{2cosx - \sin x + 4} \Rightarrow t(2cosx - \sin x + 4) = 3sinx - \cos x - 1

    \Leftrightarrow (2t + 1)cosx - (t + 3)sinx = - (4t + 1).

    Phương trình trên có nghiệm khi

    (2t + 1)^{2} + (t + 3)^{2} \geq (4t + 1)^{2}

    \Leftrightarrow \frac{- 9}{11} \leq t \leq 1 \Rightarrow 2 \leq |t| + 2 \leq 3.

    Nhìn vào hình trên ta thấy hàm số f(x) luôn đồng biến trên \lbrack 2\ ;\ 3brack nên phương trình f\left( \left| \frac{3sinx - \cos x - 1}{2cosx - \sin x + 4} ight| + 2 ight) = f\left( \sqrt{(m + 2)^{2} + 4} ight) hay phương trình f\left( |t| + 2 ight) = f\left( \sqrt{(m + 2)^{2} + 4} ight) có nghiệm khi và chỉ khi phương trình |t| + 2 = \sqrt{(m + 2)^{2} + 4} có nghiệm t thỏa mãn điều kiện 2 \leq |t| + 2 \leq 3

    \Leftrightarrow 2 \leq \sqrt{(m + 2)^{2} + 4} \leq 3 \Rightarrow m^{2} + 4m - 1 \leq 0 \Leftrightarrow - 2 - \sqrt{5} \leq m \leq - 2 + \sqrt{5}

    Mà m\mathbb{\in Z} nên có tất cả 5 giá trị m thỏa mãn.

  • Câu 12: Vận dụng cao
    Xác định số nghiệm thực của phương trình

    Cho hàm số f(x) có đồ thị là đường cong như hình vẽ bên dưới.

    Số nghiệm thực phân biệt của phương trình f\left( x^{3}f(x) \right) + 1 = 0 là

    Hướng dẫn:

    Dựa vào đồ thị, ta thấy f\left( x^{3}f(x) ight) + 1 = 0

    \Leftrightarrow f\left( x^{3}f(x) ight) = - 1

    \Leftrightarrow \left\lbrack \begin{matrix} x^{3}f(x) = a \in ( - 6; - 5)(1) \\ x^{3}f(x) = b \in ( - 3; - 2)(2) \\ x^{3}f(x) = 0(3) \\ \end{matrix} ight.

    + Phương trình (3) tương đương \left\lbrack \begin{matrix} x = 0 \\ f(x) = 0 \\ \end{matrix} ight.

    \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = x_{1},\left( - 6 < x_{1} < a < - 5 ight) \\ \end{matrix} ight.

    + Các hàm số g(x) = \frac{a}{x^{3}} và h(x) = \frac{b}{x^{3}} đồng biến trên các khoảng ( - \infty;0) và (0; + \infty), và nhận xét rằng x = 0 không phải là nghiệm của phương trình (1) nên: (1) \Leftrightarrow \left\lbrack \begin{matrix} f(x) = g(x) \\ f(x) = h(x) \\ \end{matrix} ight..

    + Trên khoảng ( - \infty;0), ta có \left\{ \begin{matrix} \lim_{x ightarrow - \infty}f(x) = + \infty;\lim_{x ightarrow 0^{-}}f(x) = - 1 \\ \lim_{x ightarrow - \infty}g(x) = \lim_{x ightarrow - \infty}h(x) = 0 \\ \lim_{x ightarrow 0^{-}}g(x) = \lim_{x ightarrow 0^{-}}h(x) = + \infty \\ \end{matrix} ight.

    nên các phương trình f(x) = g(x) và f(x) = h(x) có nghiệm duy nhất.

    + Trên khoảng (0; + \infty), ta có \left\{ \begin{matrix} \lim_{x ightarrow + \infty}f(x) = - \infty;\lim_{x ightarrow 0^{+}}f(x) = - 1 \\ \lim_{x ightarrow + \infty}g(x) = \lim_{x ightarrow + \infty}h(x) = 0 \\ \lim_{x ightarrow 0^{+}}g(x) = \lim_{x ightarrow 0^{+}}h(x) = - \infty \\ \end{matrix} ight.

    nên các phương trình f(x) = g(x) và f(x) = h(x) có nghiệm duy nhất.

    Do đó, phương trình f\left( x^{3}f(x) ight) + 1 = 0 có 6 nghiệm phân biệt.

  • Câu 13: Thông hiểu
    Tìm m để bất phương trình nghiệm đúng với mọi m

    Cho hàm số y = f(x). Hàm số y = f'(x) có đồ thị như hình bên. Biết f( - 1) = 1;f\left( - \frac{1}{e} \right) = 2. Tìm tất cả các giá trị của m để bất phương trình f(x) < \ln( - x) + m nghiệm đúng với mọi x \in \left( - 1;\frac{- 1}{e} \right).

    Hướng dẫn:

    Ta có f(x) < \ln( - x) + m \Leftrightarrow m > f(x) - \ln( - x).

    Xét hàm số g(x) = f(x) - \ln( - x) trên \left( - 1; - \frac{1}{e} ight).

    Có g'(x) = f'(x) - \frac{1}{x}.

    Trên \left( - 1; - \frac{1}{e} ight) có f'(x) > 0 và \frac{1}{x} < 0 nên g'(x) > 0,\forall x \in \left( - 1; - \frac{1}{e} ight)

    \Rightarrow Hàm số g(x) đồng biến trên \left( - 1; - \frac{1}{e} ight).

    Vậy nên f(x) < \ln( - x) + m nghiệm đúng với mọi x \in \left( - 1; - \frac{1}{e} ight)

    \Leftrightarrow m \geq g(x),\forall x \in \left( - 1; - \frac{1}{e} ight)

    \Leftrightarrow m \geq g\left( - \frac{1}{e} ight)

    \Leftrightarrow m \geq 3.

  • Câu 14: Vận dụng cao
    Chọn phương án thích hợp

    Cho hàm số y = f(x) liên tục trên \mathbb{R} và có đồ thị như hình vẽ. Số nghiệm trên khoảng ( - \pi;4\pi) của phương trình f\left( 2|cos2x| \right) = 1 là

    Hướng dẫn:

    Đặt t = 2|cos2x|.

    Vì x \in ( - \pi;4\pi) nên t \in \lbrack 0;2brack

    Phương trình trở thành: f(t) = 1.

    Từ đồ thị hàm số ta suy ra phương trình f(t) = 1 có các nghiệm thuộc \lbrack 0;2brack là \left\lbrack \begin{matrix} t = 1 \\ t = 2 \\ \end{matrix} ight..

    Với t = 1 \Leftrightarrow |cos2x| = \frac{1}{2} \Leftrightarrow \left\lbrack \begin{matrix} cos2x = \frac{1}{2} \\ cos2x = \frac{- 1}{2} \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} x = \frac{\pm \pi}{6} + k\pi \\ x = \frac{\pm \pi}{3} + k\pi \\ \end{matrix} ight.

    Vì x \in ( - \pi;2\pi) \Rightarrow \left\lbrack \begin{matrix} - \pi < \frac{\pi}{6} + k\pi < 4\pi \\ - \pi < \frac{- \pi}{6} + k\pi < 4\pi \\ - \pi < \frac{\pi}{3} + k\pi < 4\pi \\ - \pi < \frac{- \pi}{3} + k\pi < 4\pi \\ \end{matrix} ight. \Leftrightarrow \left\lbrack \begin{matrix} \frac{- 7}{6} < k < \frac{23}{6} \\ \frac{- 5}{6} < k < \frac{25}{6} \\ \frac{- 4}{3} < k < \frac{11}{3} \\ \frac{- 2}{3} < k < \frac{13}{3} \\ \end{matrix} ight.

    \Rightarrowphương trình có 20 nghiệm thuộc khoảng ( - \pi;4\pi).

    Với t = 2 \Leftrightarrow \left\lbrack \begin{matrix} cos2x = 1 \\ cos2x = - 1 \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} x = k\pi \\ x = \frac{\pi}{2} + k\pi \\ \end{matrix} ight.

    Vì x \in ( - \pi;2\pi) \Rightarrow \left\lbrack \begin{matrix} - \pi < k\pi < 4\pi \\ - \pi < \frac{\pi}{2} + k\pi < 4\pi \\ \end{matrix} ight. \Leftrightarrow \left\lbrack \begin{matrix} - 1 < k < 4 \\ \frac{- 3}{2} < k < \frac{7}{2} \\ \end{matrix} ight.

    \Rightarrowphương trình có 9nghiệm thuộc khoảng ( - \pi;4\pi).

    Vậy phương trình đã cho có tất cả 29 nghiệm.

  • Câu 15: Vận dụng cao
    Tìm số giá trị nguyên của tham số m

    Cho hàm số f(x) liên tục trên \mathbb{R} và có đồ thị như hình vẽ. Số giá trị nguyên của tham số m để phương trình f^{2}\left( \cos x \right) + (m - 2022)f\left( \cos x \right) + m - 2023 = 0 có đúng 6 nghiệm phân biệt thuộc đoạn \lbrack 0;2\pi\rbrack là

    Hướng dẫn:

    Ta có f^{2}\left( \cos x ight) + (m - 2022)f\left( \cos x ight) + m - 2023 = 0

    \Leftrightarrow \left\lbrack \begin{matrix} f\left( \cos x ight) = - 1 \\ f\left( \cos x ight) = 2023 - m \\ \end{matrix} ight. (1)

    * Với f\left( \cos x ight) = - 1

    Dựa vào đồ thị ta có f\left( \cos x ight) = - 1

    \Leftrightarrow \left\lbrack \begin{matrix} \cos x = 0 \\ \cos x = x_{1};\left( x_{1} > 1 ight)(VN) \\ \end{matrix} ight.

    \Leftrightarrow x = \frac{\pi}{2} + k\pi

    Vì x \in \lbrack 0;2\pibrack \Rightarrow x \in \left\{ \frac{\pi}{2};\frac{3\pi}{2} ight\}

    * Với f\left( \cos x ight) = 2023 - m

    Đặt t = \cos x\ \ \left( t \in \lbrack - 1;1brack ight)

    Với t \in ( - 1;1brack thì phương trình t = \cos x có hai nghiệm phân biệt thuộc \lbrack 0;2\pibrack.

    Với t = - 1 thì phương trình t = \cos x có một nghiệm thuộc \lbrack 0;2\pibrack

    Phương trình trở thành f(t) = 2023 - m

    Để phương trình (1) có tất cả 6 nghiệm phân biệt thì phương trình f\left( \cos x ight) = 2023 - m có 4 nghiệm phân biệt, hay phương trình f(t) = 2023 - m có hai nghiệm t \in ( - 1;1brack

    Dựa vào đồ thị ta có để phương trình f(t) = 2023 - m có hai nghiệm t \in ( - 1;1brack thì - 1 < 2023 - m \leq 1 \Leftrightarrow 2022 \leq m < 2024

    Vì m nguyên nên m \in \left\{ 2022;2023 ight\}

    Vậy có 2 giá trị nguyên của m thỏa mãn.

  • Câu 16: Thông hiểu
    Tìm điều kiện tham số m để bất phương trình nghiệm đúng

    Cho hàm số y = f(x), hàm số y = f'(x) liên tục trên \mathbb{R} và có đồ thị như hình vẽ bên. Bất phương trình f(x) > x^{2} - 2x + m (m là tham số thực) nghiệm đúng với mọi x \in (1;2) khi và chỉ khi

    Hướng dẫn:

    Minh họa đồ thị như hình vẽ dưới đây:

    Ta có: f(x) > x^{2} - 2x + m\left( \forall x \in (1;2) ight)

    \Leftrightarrow f(x) - x^{2} + 2x > m\left( \forall x \in (1;2) ight)(*).

    Gọi g(x) = f(x) - \left( x^{2} - 2x ight)

    \Rightarrow g'(x) = f'(x) - (2x - 2)

    Theo đồ thị ta thấy f'(x) < (2x - 2)\left( \forall x \in \lbrack 1;2brack ight) \Rightarrow g'(x) < 0\left( \forall x \in \lbrack 1;2brack ight).

    Vậy hàm số y = g(x) liên tục và nghịch biến trên \lbrack 1;2brack

    Do đó (*) \Leftrightarrow m \leq \min_{\lbrack 1;2brack}g(x) = g(2) = f(2).

  • Câu 17: Thông hiểu
    Định m để bất phương trình nghiệm đúng với mọi x

    Cho hàm số y = f(x) liên tục trên \mathbb{R} và thỏa mãn f( - 1) = 1,\ \ f\left( - \frac{1}{e} \right) = 2. Hàm số f'(x) có đồ thị như hình vẽ. Bất phương trình f(x) < \ln( - x) + x^{2} + m nghiệm đúng với mọi x \in \left( - 1; - \frac{1}{e} \right) khi và chỉ khi

    Hướng dẫn:

    Điều kiện: - x > 0 \Leftrightarrow x < 0

    Bất phương trình đã cho tương đương với f(x) - \ln( - x) - x^{2} < m (*).

    Xét hàm số g(x) = f(x) - \ln( - x) - x^{2} trên \left( - 1; - \frac{1}{e} ight).

    Ta có g'(x) = f'(x) - \frac{1}{x} - 2x. Với x \in \left( - 1; - \frac{1}{e} ight) thì f'(x) > 0; - \frac{1}{x} - 2x > 0 nên g'(x) > 0.

    Do đó hàm số g(x) đồng biến trên \left( - 1; - \frac{1}{e} ight).

    Suy ra (*) nghiệm đúng với mọi x \in \left( - 1; - \frac{1}{e} ight) khi và chỉ khi m \geq g\left( - \frac{1}{e} ight) = f\left( - \frac{1}{e} ight) - \ln\frac{1}{e} - \frac{1}{e^{2}} = 3 - \frac{1}{e^{2}}.

  • Câu 18: Vận dụng cao
    Tìm điều kiện cần và đủ của tham số m theo yêu cầu

    Cho hàm số y = f(x). Đồ thị hàm số y = f'(x) như hình vẽ. Cho bất phương trình 3f(x) \geq x^{3} - 3x + m (m là tham số thực). Điều kiện cần và đủ để bất phương trình 3f(x) \geq x^{3} - 3x + m đúng với mọi x \in \left\lbrack - \sqrt{3};\sqrt{3} \right\rbrack là

    Hướng dẫn:

    Ta có 3f(x) \geq x^{3} - 3x + m \Leftrightarrow 3f(x) - x^{3} + 3x \geq m

    Đặt g(x) = 3f(x) - x^{3} + 3x. Tính g'(x) = 3f'(x) - 3x^{2} + 3

    Có g'(x) = 0 \Leftrightarrow f'(x) = x^{2} - 1

    Nghiệm của phương trình g'(x) = 0 là hoành độ giao điểm của đồ thị hàm số y = f'(x) và parabol y = x^{2} - 1

    Dựa vào đồ thị hàm số ta có: f'(x) = x^{2} - 1 \Leftrightarrow \left\lbrack \begin{matrix} x = - \sqrt{3} \\ x = 0 \\ x = \sqrt{3} \\ \end{matrix} ight.

    BBT

    Để bất phương trình nghiệm đúng với mọi x \in \left\lbrack - \sqrt{3};\sqrt{3} ightbrack thì m \leq \min_{\left\lbrack - \sqrt{3};\sqrt{3} ightbrack}g(x) = g\left( \sqrt{3} ight) = 3f\left( \sqrt{3} ight).

  • Câu 19: Thông hiểu
    Tính tổng các phần tử tập S

    Cho hàm số y = f(x) liên tục trên \mathbb{R} và có đồ thị như hình vẽ bên dưới. Gọi S là tập hợp tất cả giá trị nguyên của tham số m để phương trình f\left( \sin x \right) - m + 2 = 2sinx có nghiệm thuộc khoảng (0;\pi). Tổng các phần tử của S bằng

    Hướng dẫn:

    Đặt t = \sin x, với \ \ x \in (0;\pi) \Rightarrow t \in (0;1brack.

    Ta được phương trình: f(t) - 2t = m - 2 \Leftrightarrow f(t) = 2t + m - 2 (1)

    Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số y = f(t) và đường thẳng y = 2t + m - 2\ \ \ \ (r).

    Gọi (p):y = 2x + 1 song song với đường thẳng (\Delta):y = 2t và đi qua điểm A(0;1).

    Gọi q:y = 2x - 3 song song với đường thẳng (\Delta):y = 2t và đi qua điểm B(1; - 1).

    Để phương trình f\left( \sin x ight) - m + 2 = 2sinx có nghiệm thuộc khoảng (0;\pi) thì phương trình (1) phải có nghiệm t \in (0;1brack, suy ra đường thẳng r nằm trong miền nằm giữa hai đường thẳng q và p( có thể trùng lên q và bỏ p)

    \Rightarrow - 3 \leq m - 2 < 1 \Leftrightarrow - 1 \leq m < 3 \Rightarrow m \in \left\{ - 1;0;1;2 ight\} \Rightarrow S = \left\{ - 1;0;1;2 ight\}.

    Do đó tổng các phần tử là: - 1 + 0 + 1 + 2 = 2.

  • Câu 20: Vận dụng cao
    Xác định tất cả giá trị nguyên tham số m thỏa mãn điều kiện

    Cho hàm số f(x) = x^{3} + x + 2. Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình f\left( \sqrt[3]{f^{3}(x) + f(x) + m} \right) = - x^{3} - x + 2 có nghiệm x \in \lbrack - 1;2\rbrack?

    Hướng dẫn:

    Xét hàm số f(t) = t^{3} + t + 2, ta có f'(t) = 3t^{2} + 1 > 0,\forall t\mathbb{\in R}.

    Do đó hàm số f đồng biến trên \mathbb{R}.

    Ta có f\left( \sqrt[3]{f^{3}(x) + f(x) + m} ight) = f( - x)

    \Leftrightarrow - x = \sqrt[3]{f^{3}(x) + f(x) + m} \Leftrightarrow f^{3}(x) + f(x) + x^{3} + m = 0\ \ \ \ \ \ (1)

    Xét h(x) = f^{3}(x) + f(x) + x^{3} + m trên đoạn \lbrack - 1;2brack.

    Ta có h'(x) = 3f'(x) \cdot f^{2}(x) + f'(x) + 3x^{2}

    = f'(x)\left\lbrack 3f^{2}(x) + 1 ightbrack + 3x^{2}.

    Ta có f'(x) = 3x^{2} + 1 > 0,\forall x \in \lbrack - 1;2brack \Rightarrow h'(x) > 0,\forall x \in \lbrack - 1;2brack.

    Hàm số h(x) đồng biến trên \lbrack - 1;2brack nên \min_{\lbrack - 1;2brack}h(x) = h( - 1) = m - 1,\max_{\lbrack - 1;2brack}h(x) = h(2) = m +1748.

    Phương trình (1) có nghiệm khi và chỉ khi

    \begin{matrix} \mathop {\min }\limits_{[ - 1;2]} h\left( x ight) \cdot \mathop {\max }\limits_{[ - 1;2]} h\left( x ight) \leqslant 0 \Leftrightarrow h\left( { - 1} ight) \cdot h\left( 2 ight) \hfill \\ \Leftrightarrow \left( {m - 1} ight)\left( {1748 + m} ight) \leqslant 0 \hfill \\ \Leftrightarrow - 1748 \leqslant m \leqslant 1. \hfill \\ \end{matrix}

    Do m nguyên nên tập các giá trị m thỏa mãn là S = \{ - 1748; - 1747;\ldots;0;1\}.

    Vậy có tất cả 1750 giá trị nguyên của m thỏa mãn.

  • Câu 21: Vận dụng cao
    Chọn đáp án đúng

    Cho hàm số y = f(x) có bảng biến thiên như sau:

    Số nghiệm của phương trình \left| f(x + 2021) - 2022 \right| = 2023 là

    Hướng dẫn:

    Ta có :

    \left| f(x + 2021) - 2022 ight| = 2023

    \Leftrightarrow \left\lbrack \begin{matrix} f(x + 2021) - 2022 = - 2023 \\ f(x + 2021) - 2022 = 2023 \\ \end{matrix} ight.

    \Leftrightarrow \left\lbrack \begin{matrix} f(x + 2021) = - 1 \\ f(x + 2021) = 4045 \\ \end{matrix} ight..

    Từ bảng biến thiên suy ra:

    +) Phương trình: f(x + 2021) = - 1 có 3 nghiệm.

    +) Phương trình: f(x + 2021) = 4045 có 1 nghiệm.

    Vậy phương trình đã cho có 4 nghiệm.

  • Câu 22: Vận dụng
    Tìm tập hợp tham số m thỏa mãn điều kiện

    Cho hàm số y = f(x) liên tục trên \mathbb{R} và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f\left( \sin x \right) = m có nghiệm thuộc khoảng (0;\pi) là

    Hướng dẫn:

    Đặt t = \sin x \Rightarrow \forall x \in (0;\pi) \Rightarrow t \in (0;1brack

    Vậy phương trình trở thành f(t) = m.

    Dựa và đồ thị hàm số suy ra m \in \lbrack - 1;1).

0/22
22 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (23%):
    2/3
  • Thông hiểu (5%):
    2/3
  • Vận dụng (73%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
1
15 Bài viết đã được lưu

Tham khảo thêm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này
🖼️

Chuyên đề Toán 12
Xem thêm