Cách xác định vị trí tương đối giữa đường thẳng và mặt cầu
Vị trí tương đối giữa đường thẳng và mặt cầu
Trong hình học không gian, việc xác định vị trí tương đối giữa đường thẳng và mặt cầu là một kiến thức quan trọng, thường gặp trong chương trình Toán lớp 12 và các đề thi học sinh giỏi, thi THPT Quốc gia. Việc hiểu rõ các vị trí như: cắt, tiếp xúc hoặc không giao nhau sẽ giúp học sinh giải nhanh các bài toán liên quan. Bài viết dưới đây sẽ hướng dẫn bạn cách xác định vị trí tương đối giữa đường thẳng và mặt cầu một cách chi tiết, dễ hiểu, có ví dụ minh họa rõ ràng và phương pháp giải cụ thể.
A. Cách tìm vị trí tương đối của đường thẳng và mặt cầu
Để xét vị trị tương đối của 
\(d\) và \((S)\), ta sử dụng hai phương pháp sau:
a. Phương pháp hình học
Bước 1. Tính khoảng cách từ tâm \(I\) của \((S)\) đến \(d\).
Bước 2.
- Nếu \(d\lbrack I,d\rbrack >
R\) thì \(d\) không cắt \((S)\).
- Nếu \(d\lbrack I,d\rbrack = R\) thì \(d\) tiếp xúc \((S)\).
- Nếu \(d\lbrack I,d\rbrack < R\) thì \(d\) cắt \((S)\).
b. Phương pháp đại số
Bước 1. Thay \(x,\ y,\ z\) từ phương trình tham số của \(d\) vào phương trình \((S)\), khi đó ta được phương trình bậc hai theo \(t\).
Bước 2.
- Nếu phương trình bậc hai vô nghiệm \(t\) thì \(d\) không cắt \((S)\).
- Nếu phương trình bậc hai có một nghiệm \(t\) thì \(d\) tiếp xúc \((S)\).
- Nếu phương trình bậc hai có hai nghiệm \(t\) thì \(d\) cắt \((S)\).
Chú ý : Để tìm điểm chung của đường thẳng và mặt cầu ta giải phương trình bậc hai theo \(t\), sau đó thay giá trị của \(t\) vào phương trình tham số của \(d\) để tìm \((x;y;z)\).
B. Bài tập tìm vị trí tương đối giữa đường thẳng và mặt cầu
Câu 1. Trong không gian với hệ tọa độ \(Oxyz\), cho mặt cầu \((S)\) có phương trình \((x + 1)^{2} + (y - 2)^{2} + (z - 1)^{2} =
4\) và đường thẳng \(d:\left\{
\begin{matrix}
x = - 1 + 2t \\
y = 2t \\
z = 1 \\
\end{matrix} \right.\). Trong các khẳng định sau, khẳng định nào là đúng nhất?
A.\(d\) không cắt \((S)\) B. \(d\) cắt \((S)\)
C. \(d\) là tiếp tuyến của \((S)\) D. \(d\) cắt \((S)\) và đi qua tâm của \((S)\).
Hướng dẫn giải
Mặt cầu \((S)\) có tâm \(I( - 1;2;1) \notin d\) nên loại D.
Gọi \(M( - 1 + 2t;2t;1) \in d\). Thay tọa độ \(M( - 1 + 2t;2t;1)\) vào \((S)\), ta được
\(( - 1 + 2t + 1)^{2} + (2t - 2)^{2} + (1 -
1)^{2} = 4 \Leftrightarrow 8t^{2} - 8 = 0 \Leftrightarrow \left\lbrack
\begin{matrix}
t = 0 \\
t = 1 \\
\end{matrix} \right.\).
Câu 2. Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(d:\left\{ \begin{matrix}
x = - 3 \\
y = 2 + 2t \\
z = 3 + t \\
\end{matrix} \right.\) và mặt cầu \((S)\) có tâm \(I(1;2; - 2)\), đi qua gốc tọa độ \(O\). Trong các khẳng định sau, khẳng định nào đúng?
A. \(d\) là tiếp tuyến của mặt cầu \((S)\). B. \(d\) cắt \((S)\) tại hai điểm.
C. \(d\) và \((S)\) không cắt nhau. D. \(d\) song song với đường thẳng qua \(I\) và \(O\).
Hướng dẫn giải
Mặt cầu \((S)\) có bán kính \(R = OI = 3\). Suy ra \((S):(x - 1)^{2} + (y - 2)^{2} + (z + 2)^{2} =
9\).
Thay \(x,\ y,\ z\) từ phương trình đường thẳng \(d\) vào phương trình mặt cầu \((S)\), ta được
\(( - 3 - 1)^{2} + (2 + 2t - 2)^{2} + (3 +
t + 2)^{2} = 9 \Leftrightarrow 5t^{2} + 10t + 32 = 0\): vô nghiệm.
Câu 3. Trong không gian với hệ tọa độ \(Oxyz\), cho mặt cầu
\((S):(x - 1)^{2} + (y + 2)^{2} + (z -
3)^{2} = 25\) và đường thẳng \(d:\left\{ \begin{matrix}
x = 2 + 4t \\
y = 5 + 3t \\
z = 4 + t \\
\end{matrix} \right.\).
Khẳng định nào sau đây là đúng nhất:
A. \((d)\) tiếp xúc với \((S)\) tại \(M( -
2;2;3)\). B. \((d)\) và \((S)\) không cắt nhau.
C. \((d)\) cắt \((S)\) tại hai điểm. D. \((d)\) cắt \((S)\) và đi qua tâm của \((S)\).
Hướng dẫn giải
Thay \(x,\ y,\ z\) từ phương trình đường thẳng \(d\) vào phương trình mặt cầu \((S)\), ta được
\((2 + 4t - 1)^{2} + (5 + 3t + 2)^{2} + (4
+ t - 3)^{2} = 25 \Leftrightarrow 26t^{2} + 52t + 26 = 0 \Leftrightarrow
t = - 1\).
Suy ra \((d)\) tiếp xúc với \((S)\) tại \(M( -
2;2;3)\)
Câu 4. Trong không gian \(Oxyz\), cho điểm \(I(1\ ;0\ ;2)\) và đường thẳng \(d:\ \frac{x - 1}{2} = \frac{y}{- 1} =
\frac{z}{1}\). Gọi \((S)\) là mặt cầu có tâm \(I\), tiếp xúc với đường thẳng \(d\). Bán kính của \((S)\) bằng
A. \(\frac{5}{3}\). B. \(\frac{2\sqrt{5}}{3}\). C. \(\frac{\sqrt{30}}{3}\). D. \(\frac{4\sqrt{2}}{3}\).
Hướng dẫn giải
Gọi \(H(1 + 2t\ ; - t\ ;t)\) là hình chiếu của \(I\) trên đường thẳng \(d\).
Có \(\overrightarrow{IH} = (2t\ ; - t\ ;t -
2)\); vectơ chỉ phương của \(d\) là \(\overrightarrow{u} = (2\ ; - 1\
;1)\).
Vì \(H\) là hình chiếu vuông góc của \(I\) trên \(d\) nên \(\overrightarrow{IH}\bot\overrightarrow{u}
\Leftrightarrow \overrightarrow{IH}.\overrightarrow{u} = 0\)
\(\Leftrightarrow 2t.2 + ( - t).( - 1) + (t
- 2).1 = 0 \Leftrightarrow t = \frac{1}{3} \Rightarrow
\overrightarrow{IH} = \left( \frac{2}{3}\ ; - \frac{1}{3}\ ; -
\frac{5}{3} \right) \Rightarrow IH = \frac{\sqrt{30}}{3}\).
Bán kính của mặt cầu \((S)\) là \(R = IH = \frac{\sqrt{30}}{3}\).
Câu 5. Trong không gian \(Oxyz\), cho mặt cầu \((S):\ \ x^{2} + y^{2} + z^{2} +
4x - 6y + m = 0\) (\(m\) là tham số) và đường thẳng \(\Delta:\ \ \left\{
\begin{matrix}
x = 4 + 2t \\
y = 3 + t \\
z = 3 + 2t \\
\end{matrix} \right.\). Biết đường thẳng \(\Delta\) cắt mặt cầu \((S)\) tại hai điểm phân biệt \(A\ ,\ B\) sao cho \(AB = 8\). Giá trị của \(m\) là
A. \(m = 5\). B. \(m = 12\). C. \(m
= - 12\). D. \(m = - 10\).
Hướng dẫn giải
Hình vẽ minh họa
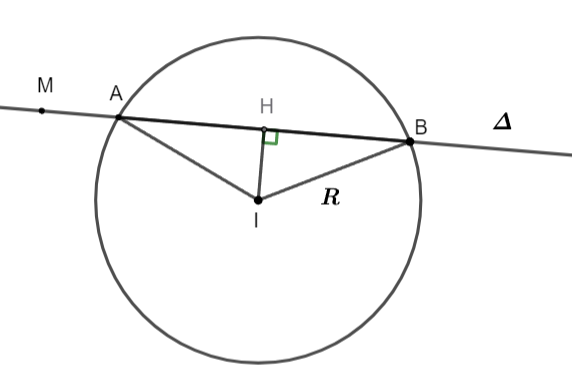
Gọi \(H\) là trung điểm đoạn thẳng \(AB \Rightarrow IH\bot AB\ \ ,\ \ HA =
4\).
Mặt cầu \((S)\) có tâm \(I( - 2\ \ ;\ \ 3\ \ ;\ \ 0)\), bán kính \(R = \sqrt{13 - m}\ ,\ \ (m <
13)\).
Đường thẳng \(\Delta\) đi qua \(M(4\ \ ;\ \ 3\ \ ;\ \ 3)\) và có 1 véc tơ chỉ phương \(\overrightarrow{u} = (2\ \ ;\ \
1\ \ ;\ \ 2)\).
Ta có: \(\overrightarrow{IM} = (6;0;3)
\Rightarrow \left\lbrack \overrightarrow{IM},\overrightarrow{u}
\right\rbrack = ( - 3; - 6;6)\)
\(\Rightarrow IH = d(I,\Delta) =
\frac{\left| \left\lbrack \overrightarrow{IM},\overrightarrow{u}
\right\rbrack \right|}{\left| \overrightarrow{u} \right|} =
3\)
Ta có: \(R^{2} = IH^{2} + HA^{2}
\Leftrightarrow 13 - m = 3^{2} + 4^{2} \Leftrightarrow m = -
12\).
-------------------------------------------------
Trên đây là toàn bộ kiến thức cần nắm về cách xác định vị trí tương đối giữa đường thẳng và mặt cầu trong không gian. Hy vọng bài viết đã giúp bạn hiểu rõ bản chất từng trường hợp và biết cách vận dụng công thức để giải bài toán nhanh chóng và chính xác. Hãy luyện tập thường xuyên với các dạng bài liên quan để củng cố kiến thức và đạt điểm cao trong các kỳ thi nhé!
