Công thức tính góc trong không gian
Cách tính góc trong không gian Oxyz
Trong hình học không gian, việc tính góc giữa các yếu tố như đường thẳng, mặt phẳng là kỹ năng quan trọng, xuất hiện thường xuyên trong các bài kiểm tra, đề thi THPT Quốc gia và học sinh giỏi. Tuy nhiên, không ít học sinh gặp khó khăn trong việc ghi nhớ và vận dụng đúng các công thức tính góc trong không gian. Bài viết này sẽ hệ thống đầy đủ các công thức tính góc giữa hai đường thẳng, giữa đường thẳng và mặt phẳng, giữa hai mặt phẳng… cùng ví dụ minh họa và hướng dẫn chi tiết từng bước giải bài toán.
A. Công thức tính góc giữa hai vectơ
Cho hai vectơ 
\(\overrightarrow{a} =
(a_{1};a_{2};a_{3})\) và \(\overrightarrow{b} = (b_{1};b_{2};b_{3}).\) Khi đó góc giữa hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) là góc nhọn hoặc tù.
\(\boxed{cos(\overrightarrow{a};\overrightarrow{b})
= \frac{\overrightarrow{a}.\overrightarrow{b}}{\left| \overrightarrow{a}
\right|.\left| \overrightarrow{b} \right|} = \frac{a_{1}b_{1} +
a_{2}b_{2} + a_{3}b_{3}}{\sqrt{a_{1}^{2} + a_{2}^{2} +
a_{3}^{2}}.\sqrt{b_{1}^{2} + b_{2}^{2} + b_{3}^{2}}}}\)
Với \(0{^\circ} < \alpha <
180{^\circ}.\)
B. Công thức tính góc giữa hai đường thẳng
Hình vẽ minh họa
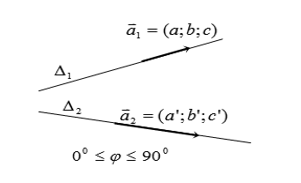
Trong không gian \(Oxyz\), cho hai đường thẳng \(d_{1},\ d_{2}\) lần lượt có các VTPT là \(\overrightarrow{u_{1}},\
\overrightarrow{u_{2}}\).
Góc giữa \(d_{1}\) và \(d_{2}\) bằng hoặc bù với góc giữa \(\overrightarrow{u_{1}}\) và \(\overrightarrow{u_{2}}\).
Tức là:
\(\cos\left( d_{1},d_{2} \right) =
\left| \cos\left( \overrightarrow{u_{1}}.\overrightarrow{u_{2}} \right)
\right| = \frac{\left| \overrightarrow{u_{1}}.\overrightarrow{u_{2}}
\right|}{\left| \overrightarrow{u_{1}} \right|.\left|
\overrightarrow{u_{2}} \right|}\)
C. Công thức góc giữa đường thẳng và mặt phẳng
Hình vẽ minh họa
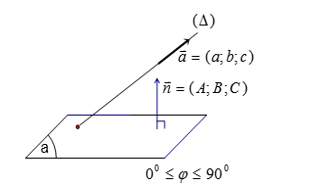
Trong không gian \(Oxyz\), cho đường thẳng \(d\) có VTCP \(\overrightarrow{u_{d}}\) và mặt phẳng \((\alpha)\) có VTPT \(\overrightarrow{n_{\alpha}}\).
Góc giữa đường thẳng \(d\) và mặt phẳng \((\alpha)\) bằng góc giữa đường thẳng \(d\) với hình chiếu \(d'\) của nó trên \((\alpha)\).
Tức là:
\(\sin\left( d,(\alpha) \right) =
\left| \cos\left( \overrightarrow{u_{d}},\overrightarrow{n_{\alpha}}
\right) \right| = \frac{\left|
\overrightarrow{u_{d}}.\overrightarrow{n_{\alpha}} \right|}{\left|
\overrightarrow{u_{d}} \right|.\left| \overrightarrow{n_{\alpha}}
\right|}\)
---------------------------------------------------------
Trên đây là toàn bộ công thức tính góc trong không gian mà bạn cần nắm vững để học tốt hình học lớp 12 và chinh phục các kỳ thi quan trọng. Việc thành thạo các công thức và luyện tập thường xuyên sẽ giúp bạn giải quyết nhanh chóng các dạng bài phức tạp liên quan đến góc. Đừng quên lưu lại bài viết và chia sẻ để cùng bạn bè học tập hiệu quả hơn nhé!
