Phương pháp xác định vị trí tương đối trong hình học không gian
Cách xác định vị trí tương đối trong hình học khôn gian
Trong hình học không gian, việc xác định vị trí tương đối giữa các yếu tố như đường thẳng – đường thẳng, đường thẳng – mặt phẳng và đường thẳng – mặt cầu là kiến thức nền tảng và vô cùng quan trọng. Việc phân loại đúng các vị trí như: song song, cắt nhau, trùng nhau, chéo nhau… giúp học sinh giải quyết chính xác các bài toán hình học phức tạp trong chương trình Toán lớp 12 và ôn thi THPT Quốc gia. Bài viết này sẽ giúp bạn hệ thống toàn bộ kiến thức về vị trí tương đối trong không gian, kèm ví dụ minh họa, công thức và phương pháp làm bài hiệu quả.
A. Vị trí tương đối giữa hai đường thẳng
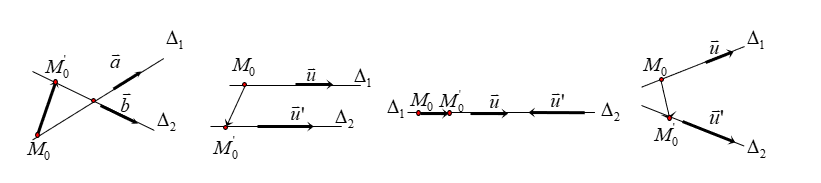
Trong không gian 
\(Oxyz\), cho hai đường thẳng \(d_{1}:\frac{x - x_{0}}{a} =
\frac{y - y_{0}}{b} = \frac{z - z_{0}}{c}\) đi qua \(M_{1}\left( x_{0};y_{0};z_{0} \right)\) có VTCP \(\overrightarrow{u_{1}} =
(a;b;c)\) và \(d_{2}:\frac{x -
x_{0}^{,}}{a'} = \frac{y - y_{0}^{,}}{b'} = \frac{z -
z_{0}^{,}}{c'}\) đi qua \(M_{2}\left( x_{0}^{,};y_{0}^{,};z_{0}^{,}
\right)\) có VTCP \(\overrightarrow{u_{2}} =
(a';b';c')\).
Để xét vị trị tương đối của \(d_{1}\) và \(d_{2}\), ta sử dụng hai phương pháp sau:
Phương pháp hình học:
- \(d_{1} \equiv d_{2}\ \Leftrightarrow \
\left\lbrack \overrightarrow{u_{1}},\overrightarrow{u_{2}} \right\rbrack
= \left\lbrack \overrightarrow{u_{1}},\overrightarrow{M_{1}M_{2}}
\right\rbrack = \overrightarrow{0}\) hoặc \(\left\{ \begin{matrix}
\overrightarrow{u_{1}} \parallel \overrightarrow{u_{2}} \\
M_{1} \in d_{2} \\
\end{matrix} \right.\ \ \Leftrightarrow \ \left\{ \begin{matrix}
\frac{a_{1}}{b_{1}} = \frac{a_{2}}{b_{2}} = \frac{a_{3}}{b_{3}} \\
M_{1} \in d_{2} \\
\end{matrix} \right.\).
- \(d_{1} \parallel d_{2}\ \Leftrightarrow
\ \left\{ \begin{matrix}
\left\lbrack \overrightarrow{u_{1}},\overrightarrow{u_{2}} \right\rbrack
= \overrightarrow{0} \\
\left\lbrack \overrightarrow{u_{1}},\overrightarrow{M_{1}M_{2}}
\right\rbrack \neq \overrightarrow{0} \\
\end{matrix} \right.\) hoặc \(\left\{
\begin{matrix}
\overrightarrow{u_{1}} \parallel \overrightarrow{u_{2}} \\
M_{1} \notin d_{2} \\
\end{matrix} \right.\ \ \Leftrightarrow \ \left\{ \begin{matrix}
\frac{a_{1}}{b_{1}} = \frac{a_{2}}{b_{2}} = \frac{a_{3}}{b_{3}} \\
M_{1} \notin d_{2} \\
\end{matrix} \right.\).
- \(d_{1}\) cắt \(d_{2} \Leftrightarrow \ \left\{ \begin{matrix}
\left\lbrack \overrightarrow{u_{1}},\overrightarrow{u_{2}} \right\rbrack
\neq \overrightarrow{0} \\
\left\lbrack \overrightarrow{u_{1}},\overrightarrow{u_{2}}
\right\rbrack.\overrightarrow{M_{1}M_{2}} = 0 \\
\end{matrix} \right.\).
- \(d_{1}\) chéo \(d_{2} \Leftrightarrow \ \left\lbrack
\overrightarrow{u_{1}},\overrightarrow{u_{2}}
\right\rbrack.\overrightarrow{M_{1}M_{2}} \neq 0\).
Phương pháp đại số:
Dựa vào số nghiệm của hệ phương trình các đường thẳng. \(\left\{ \begin{matrix}
x_{\circ} + a_{1}t = {x'}_{\circ} + {a'}_{1}t' \\
y_{\circ} + a_{2}t = {y'}_{\circ} + {a'}_{2}t' \\
z_{\circ} + a_{3}t = {z'}_{\circ} + {a'}_{3}t' \\
\end{matrix} \right.\ \ .\)
B. Vị trí tương đối giữa đường thẳng và mặt phẳng
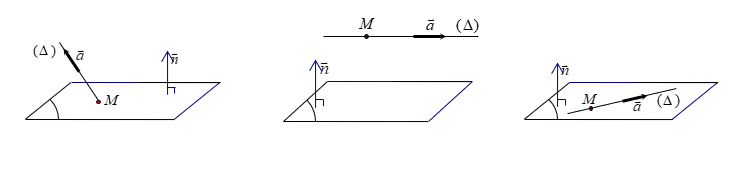
Trong không gian \(Oxyz\), cho mặt phẳng \((\alpha):Ax + By + Cz + D =
0\) có VTPT \(\overrightarrow{n_{\alpha}} = (A;B;C)\) và đường thẳng \(d:\left\{ \begin{matrix}
x = x_{0} + at \\
y = y_{0} + bt \\
z = z_{0} + ct \\
\end{matrix} \right.\) đi qua \(M\left( x_{0};y_{0};z_{0} \right)\), có VTCP \(\overrightarrow{u_{d}} =
(a;b;c)\).
Để xét vị trị tương đối của \(d\) và \((\alpha)\), ta sử dụng hai phương pháp sau:
Phương pháp hình học:
- Nếu \(\left\{ \begin{matrix}
\overrightarrow{u_{d}}\bot\overrightarrow{n_{\alpha}} \\
M\left( x_{0};y_{0};z_{0} \right) \in (\alpha) \\
\end{matrix} \right.\) thì \(d
\subset (\alpha)\).
- Nếu \(\left\{ \begin{matrix}
\overrightarrow{u_{d}}\bot\overrightarrow{n_{\alpha}} \\
M\left( x_{0};y_{0};z_{0} \right) \notin (\alpha) \\
\end{matrix} \right.\) thì \(d
\parallel (\alpha)\).
- Nếu \(\overrightarrow{u_{d}}\) không cùng phương với \(\overrightarrow{n_{\alpha}}\) thì \(d\) cắt \((\alpha)\).
- \(d\bot(\alpha) \Leftrightarrow \
\overrightarrow{u_{d}}\) và \(\overrightarrow{n_{\alpha}}\) cùng phương \(\overrightarrow{u_{d}} =
k.\overrightarrow{n_{\alpha}}\) với \(k\neq 0\).
Phương pháp đại số:
Xét hệ phương trình \(\left\{
\begin{matrix}
x = x_{o} + at & (1) \\
y = y_{o} + bt & (2) \\
z = z_{o} + ct & (3) \\
Ax + By + Cz + D = 0 & (4) \\
\end{matrix} \right.\) .
Thay \((1),\ (2),\ (3)\) vào \((4)\), ta được
\(A\left( x_{o} + at \right) + B\left(
y_{o} + bt \right) + C\left( z_{o} + ct \right) + D = 0\)
\(\Leftrightarrow (Aa + Bb + Cc)t = -
\left( D + Ax_{0} + By_{0} + Cz_{0} \right)\). \((*)\)
Phương trình \((*)\) là phương trình bậc nhất, ẩn \(t\). Ta có
- Nếu phương trình \((*)\) vô nghiệm \(t\) thì \(d
\parallel (\alpha)\).
- Nếu phương trình \((*)\) có nghiệm \(t\) duy nhất thì \(d\) cắt \((\alpha)\).
- Nếu phương trình \((*)\) có vô số nghiệm \(t\) thì \(d \subset (\alpha)\).
Chú ý: Để tìm điểm chung của đường thẳng và mặt phẳng ta giải phương trình bậc nhất theo \(t\), sau đó thay giá trị của \(t\) vào phương trình tham số của \(d\) để tìm \((x;y;z)\).
C. Vị trí tương đối giữa đường thẳng và mặt cầu
Trong không gian \(Oxyz\), cho đường thẳng và mặt cầu \(d:\left\{ \begin{matrix}
x = x_{0} + at \\
y = y_{0} + bt \\
z = z_{0} + ct \\
\end{matrix} \right.\ \ ,\ t\mathbb{\in R}\)
và \((S):(x - a)^{2} + (y - b)^{2} + (z -
c)^{2} = R^{2}\).
Để xét vị trị tương đối của \(d\) và \((\alpha)\), ta sử dụng hai phương pháp sau:
Phương pháp hình học:
Bước 1. Tính khoảng cách từ tâm \(I\) của \((S)\) đến \(d\).
Bước 2.
+ Nếu \(d\lbrack I,d\rbrack >
R\) thì \(d\) không cắt \((S)\).
+ Nếu \(d\lbrack I,d\rbrack = R\) thì \(d\) tiếp xúc \((S)\).
+ Nếu \(d\lbrack I,d\rbrack < R\) thì \(d\) cắt \((S)\).
Phương pháp đại số:
• Bước 1. Thay \(x,\ y,\ z\) từ phương trình tham số của \(d\) vào phương trình \((S)\), khi đó ta được phương trình bậc hai theo \(t\).
• Bước 2.
+ Nếu phương trình bậc hai vô nghiệm \(t\) thì \(d\) không cắt \((S)\).
+ Nếu phương trình bậc hai có một nghiệm \(t\) thì \(d\) tiếp xúc \((S)\).
+ Nếu phương trình bậc hai có hai nghiệm \(t\) thì \(d\) cắt \((S)\).
Chú ý : Để tìm điểm chung của đường thẳng và mặt cầu ta giải phương trình bậc hai theo \(t\), sau đó thay giá trị của \(t\) vào phương trình tham số của \(d\) để tìm \((x;y;z)\).
-----------------------------------------
Như vậy, việc nhận biết vị trí tương đối giữa đường thẳng và các đối tượng hình học trong không gian là kỹ năng bắt buộc để học tốt hình học 12. Nắm vững từng trường hợp, kết hợp phương pháp giải hình học và đại số sẽ giúp bạn làm bài nhanh và chính xác hơn. Hãy lưu lại bài viết, luyện tập thêm và chia sẻ với bạn bè để cùng học tập hiệu quả hơn nhé!
