VnDoc.com

Giải bài tập SBT Toán 12 bài 3

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Bài trước

Bài sau

Toán 12 - Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập SBT Toán 12 bài 3, tài liệu kèm theo lời giải chi tiết sẽ là nguồn thông tin hay để phục vụ công việc học tập của các bạn học sinh được tốt hơn. Mời thầy cô và các bạn học sinh cùng tham khảo.

Trắc nghiệm Toán 12 chương 1: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Giải bài tập trang 24 SGK Giải tích lớp 12: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Bài tập SBT Toán 12 bài 3

Bài 1.20 trang 19 Sách bài tập (SBT) Giải tích 12

Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:

a) f(x) = -3x² + 4x – 8 trên đoạn [0; 1]

b) f(x) = x³ + 3x² – 9x – 7 trên đoạn [-4; 3]

c) $f(x) = \sqrt {25 - {x^2}}$ $f(x) = \sqrt {25 - {x^2}}$ trên đoạn [-4; 4]

d) f(x) = |x² – 3x + 2| trên đoạn [-10; 10]

e) $f(x) = {1 \over {\sin x}}$ $f(x) = {1 \over {\sin x}}$ trên đoạn ${\rm{[}}{\pi \over 3};{{5\pi } \over 6}{\rm{]}}$ ${\rm{[}}{\pi \over 3};{{5\pi } \over 6}{\rm{]}}$

g) $f(x) = 2\sin x + \sin 2x$ $f(x) = 2\sin x + \sin 2x$ trên đoạn ${\rm{[}}0;{{3\pi } \over 2}{\rm{]}}$ ${\rm{[}}0;{{3\pi } \over 2}{\rm{]}}$

Hướng dẫn làm bài:

a) f(x) = -3x² + 4x – 8 trên đoạn [0; 1]

$f'(x) = - 6x + 4,f'(x) = 0 < = > x = {2 \over 3}$
$f({2 \over 3}) = - {{20} \over 3},f(0) = - 8;f(1) = - 7$ $f({2 \over 3}) = - {{20} \over 3},f(0) = - 8;f(1) = - 7$

Vậy $\mathop {\min }\limits_{{\rm{[}}0;1]} f(x) = - 8;\mathop {\max }\limits_{{\rm{[}}0;1]} f(x) = - {{20} \over 3}$ $\mathop {\min }\limits_{{\rm{[}}0;1]} f(x) = - 8;\mathop {\max }\limits_{{\rm{[}}0;1]} f(x) = - {{20} \over 3}$

b) f(x) = x³ + 3x² – 9x – 7 trên đoạn [-4; 3]

$f'(x) = 3{x^2} + 6x - 9$

$f'(x) = 0 \Leftrightarrow \left[ \matrix{ x = 1 \hfill \cr x = - 3 \hfill \cr} \right.$

Hàm số đạt cực đại tại x = -3, đạt cực tiểu tại x = 1 và f_CĐ = f(-3) = 20; f_CT= f(1) = -12; f(-4) = 13; f(3) = 20.

Vậy $\mathop {\min }\limits_{{\rm{[}} - 4;3]} f(x) = - 12;\mathop {\max }\limits_{{\rm{[}} - 4;3]} f(x) = 20$ $\mathop {\min }\limits_{{\rm{[}} - 4;3]} f(x) = - 12;\mathop {\max }\limits_{{\rm{[}} - 4;3]} f(x) = 20$

c) $f(x) = \sqrt {25 - {x^2}}$ $f(x) = \sqrt {25 - {x^2}}$ trên đoạn [-4; 4]

$f'(x) = {{ - x} \over {\sqrt {25 - {x^2}} }};f'(x) > 0$ trên khoảng (-4; 0) và

f’(x) < 0 trên khoảng (0; 4).

Hàm số đạt cực đại tại x = 0 và f_CĐ = 5

Mặt khác, ta có f(-4) = f(4) = 3

Vậy $\mathop {\min }\limits_{{\rm{[}} - 4;4]} f(x) = 3;\mathop {\max }\limits_{{\rm{[}} - 4;4]} f(x) = 5$ $\mathop {\min }\limits_{{\rm{[}} - 4;4]} f(x) = 3;\mathop {\max }\limits_{{\rm{[}} - 4;4]} f(x) = 5$

d) $f(x) = |{x^2} - 3x + 2|$ $f(x) = |{x^2} - 3x + 2|$ trên đoạn [-10; 10]

Khảo sát sự biến thiên và vẽ đồ thị của hàm số g(x) = x² – 3x + 2.

Ta có:

$g'(x) = 2x - 3;g'(x) = 0 < = > x = {3 \over 2}$

Bảng biến thiên:

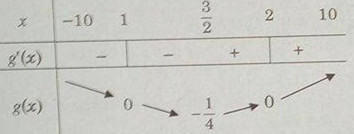
Giải bài tập SBT Toán 12 bài 3

Vì

$f(x) = \left\{ \matrix{ g(x),{x^2} - 3x + 2 \ge 0 \hfill \cr - g(x),{x^2} - 3x + 2 < 0 \hfill \cr} \right.$ $f(x) = \left\{ \matrix{ g(x),{x^2} - 3x + 2 \ge 0 \hfill \cr - g(x),{x^2} - 3x + 2 < 0 \hfill \cr} \right.$

nên ta có đồ thị f(x) như sau:

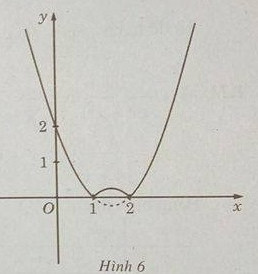
Giải bài tập SBT Toán 12 bài 3

Từ đồ thị suy ra: $\mathop {\min }\limits_{{\rm{[}} - 10;10]} f(x) = f(1) = f(2) = 0;\mathop {\max }\limits_{{\rm{[}} - 10;10]} f(x) = f( - 10) = 132$ $\mathop {\min }\limits_{{\rm{[}} - 10;10]} f(x) = f(1) = f(2) = 0;\mathop {\max }\limits_{{\rm{[}} - 10;10]} f(x) = f( - 10) = 132$

e) $f(x) = {1 \over {\sin x}}$ $f(x) = {1 \over {\sin x}}$ trên đoạn ${\rm{[}}{\pi \over 3};{{5\pi } \over 6}{\rm{]}}$ ${\rm{[}}{\pi \over 3};{{5\pi } \over 6}{\rm{]}}$

$f'(x) = - {{\cos x} \over {{{\sin }^2}x}},f'(x) < 0$ nên và f’(x) > 0 trên $({\pi \over 2};{{5\pi } \over 6}{\rm{]}}$ $({\pi \over 2};{{5\pi } \over 6}{\rm{]}}$ nên hàm số đạt cực tiểu tại $x = {\pi \over 2}$ $x = {\pi \over 2}$và ${f_{CT}} = f({\pi \over 2}) = 1$ ${f_{CT}} = f({\pi \over 2}) = 1$

Mặt khác, $f({\pi \over 3}) = {2 \over {\sqrt 3 }},f({{5\pi } \over 6}) = 2$ $f({\pi \over 3}) = {2 \over {\sqrt 3 }},f({{5\pi } \over 6}) = 2$

Vậy $\mathop {\min }\limits_{{\rm{[}}{\pi \over 3};{{5\pi } \over 6}]} f(x) = 1;\mathop {\max }\limits_{{\rm{[}}{\pi \over 3};{{5\pi } \over 6}]} f(x) = 2$ $\mathop {\min }\limits_{{\rm{[}}{\pi \over 3};{{5\pi } \over 6}]} f(x) = 1;\mathop {\max }\limits_{{\rm{[}}{\pi \over 3};{{5\pi } \over 6}]} f(x) = 2$

g) $f(x) = 2\sin x + \sin 2x$ $f(x) = 2\sin x + \sin 2x$ trên đoạn ${\rm{[}}0;{{3\pi } \over 2}{\rm{]}}$ ${\rm{[}}0;{{3\pi } \over 2}{\rm{]}}$

$f'(x) = 2\cos x + 2\cos 2x = 4\cos {x \over 2}\cos {{3x} \over 2}$

$f'(x) = 0 \Leftrightarrow \left[ \matrix{ \cos {x \over 2} = 0 \hfill \cr \cos {{3x} \over 2} = 0 \hfill \cr} \right. \Rightarrow \left[ \matrix{ x = \pi \hfill \cr x = {\pi \over 3} \hfill \cr} \right.$

Ta có: $f(0) = 0,f({\pi \over 3}) = {{3\sqrt 3 } \over 2},f(\pi ) = 0,f({{3\pi } \over 2}) = - 2$ $f(0) = 0,f({\pi \over 3}) = {{3\sqrt 3 } \over 2},f(\pi ) = 0,f({{3\pi } \over 2}) = - 2$

Từ đó ta có: $\mathop {\min }\limits_{{\rm{[}}0;{{3\pi } \over 2}]} f(x) = - 2;\mathop {\max }\limits_{{\rm{[}}0;{{3\pi } \over 2}]} f(x) = {{3\sqrt 3 } \over 2}$ $\mathop {\min }\limits_{{\rm{[}}0;{{3\pi } \over 2}]} f(x) = - 2;\mathop {\max }\limits_{{\rm{[}}0;{{3\pi } \over 2}]} f(x) = {{3\sqrt 3 } \over 2}$

Bài 1.21 trang 20 Sách bài tập (SBT) Giải tích 12

Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:

a) $y = {x \over {4 + {x^2}}}$ $y = {x \over {4 + {x^2}}}$trên khoảng $( - \infty ; + \infty ) ;$ $( - \infty ; + \infty ) ;$

b) $y = {1 \over {\cos x}}$ $y = {1 \over {\cos x}}$ trên khoảng $({\pi \over 2};{{3\pi } \over 2})$ $({\pi \over 2};{{3\pi } \over 2})$

c) $y = {1 \over {1 + {x^4}}}$ $y = {1 \over {1 + {x^4}}}$ trên khoảng $( - \infty ; + \infty ) ;$ $( - \infty ; + \infty ) ;$

d) $y = {1 \over {\sin x}}$ $y = {1 \over {\sin x}}$trên khoảng $(0;\pi ) .$ $(0;\pi ) .$

Hướng dẫn làm bài:

a) $y = {x \over {4 + {x^2}}}$ $y = {x \over {4 + {x^2}}}$ trên khoảng $( - \infty ; + \infty )$ $( - \infty ; + \infty )$

$\eqalign{ & y$ $\eqalign{ & y' = {{4 - {x^2}} \over {{{(4 + {x^2})}^2}}} \cr & y' = 0 \Rightarrow \left[ \matrix{ x = - 2 \hfill \cr x = 2 \hfill \cr} \right. \cr}$

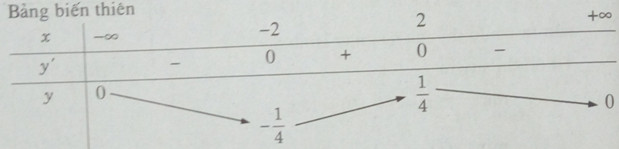
Giải bài tập SBT Toán 12 bài 3

Từ đó ta có $\mathop {\min }\limits_R f(x) = - {1 \over 4};\mathop {\max }\limits_R f(x) = {1 \over 4}$ $\mathop {\min }\limits_R f(x) = - {1 \over 4};\mathop {\max }\limits_R f(x) = {1 \over 4}$

b) $y = {1 \over {\cos x}}$ $y = {1 \over {\cos x}}$ trên khoảng $({\pi \over 2};{{3\pi } \over 2})$ $({\pi \over 2};{{3\pi } \over 2})$

$y' = {{\sin x} \over {{{\cos }^2}x}};y' = 0 < = > x = \pi$

Bảng biến thiên:

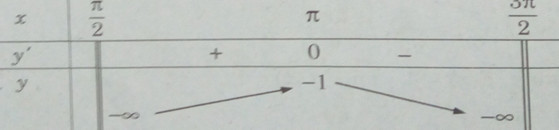
Giải bài tập SBT Toán 12 bài 3

Hàm số không có giá trị nhỏ nhất. Giá trị lớn nhất của hàm số là: $\mathop {\max }\limits_{({\pi \over 2};{{3\pi } \over 2})} y = y(\pi ) = - 1$ $\mathop {\max }\limits_{({\pi \over 2};{{3\pi } \over 2})} y = y(\pi ) = - 1$

c) $y = {1 \over {1 + {x^4}}}$ $y = {1 \over {1 + {x^4}}}$ trên khoảng $( - \infty ; + \infty )$ $( - \infty ; + \infty )$

$y' = {{ - 4{x^3}} \over {{{(1 + {x^4})}^2}}};y' = 0 < = > x = 0$

Bảng biến thiên:

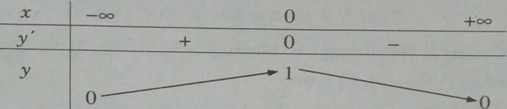
Giải bài tập SBT Toán 12 bài 3

Hàm số không có giá trị nhỏ nhất. Giá trị lớn nhất là: $\mathop {\max }\limits_R y = y(0) = 1$ $\mathop {\max }\limits_R y = y(0) = 1$

d) $y = {1 \over {\sin x}}$ $y = {1 \over {\sin x}}$ trên khoảng $(0;\pi )$ $(0;\pi )$

$y' = {{ - \cos x} \over {{{\sin }^2}x}},y' = 0 < = > x = {\pi \over 2}$

Bảng biến thiên:

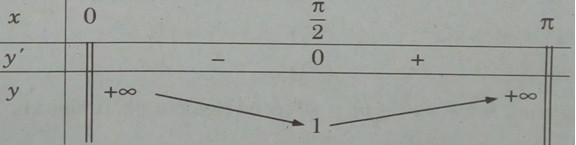
Giải bài tập SBT Toán 12 bài 3

Hàm số không có giá trị lớn nhất. Giá trị nhỏ nhất của hàm số là: $\mathop {\min }\limits_{(0;\pi )} y = y({\pi \over 2}) = 1$ $\mathop {\min }\limits_{(0;\pi )} y = y({\pi \over 2}) = 1$

Bài 1.22 trang 20 Sách bài tập (SBT) Giải tích 12

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f(x) = {{2x - 1} \over {x - 3}}$ $f(x) = {{2x - 1} \over {x - 3}}$trên đoạn [0; 2].

(Đề thi tốt nghiệp THPT năm 2008, lần 2)

Hướng dẫn làm bài:

TXĐ: D =R\{3}

$f'(x) = - {5 \over {{{(x - 3)}^2}}} < 0,\forall x \in D$và do đó f(x) nghịch biến trên các khoảng $( - \infty ;3),(3; + \infty )$ $( - \infty ;3),(3; + \infty )$

Ta thấy ${\rm{[}}0;2] \subset ( - \infty ;3)$ ${\rm{[}}0;2] \subset ( - \infty ;3)$

Vì vậy: $\mathop {\min }\limits_{{\rm{[}}0;2]} f(x) = f(2) = - 3;\mathop {\max }\limits_{{\rm{[}}0;2]} f(x) = f(0) = {1 \over 3}$ $\mathop {\min }\limits_{{\rm{[}}0;2]} f(x) = f(2) = - 3;\mathop {\max }\limits_{{\rm{[}}0;2]} f(x) = f(0) = {1 \over 3}$

Bài 1.23 trang 20 Sách bài tập (SBT) Giải tích 12

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f(x) = x + {9 \over x}$ $f(x) = x + {9 \over x}$ trên đoạn [2; 4]

(Đề thi tốt nghiệp THPT năm 2008)

Hướng dẫn làm bài:

TXĐ: D = R\{0}

$\eqalign{ & f$ $\eqalign{ & f'(x) = 1 - {9 \over {{x^2}}} = {{{x^2} - 9} \over {{x^2}}} \cr & f'(x) = 0 < = > x = \pm 3 \cr}$

Hàm số nghịch biến trong các khoảng (-3; 0), (0; 3) và đồng biến trong các khoảng $( - \infty ;3),(3; + \infty )$ $( - \infty ;3),(3; + \infty )$

Bảng biến thiên:

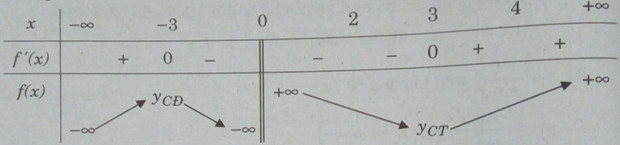
Giải bài tập SBT Toán 12 bài 3

Ta có: ${\rm{[}}2;4] \subset (0; + \infty );f(2) = 6,5;f(3) = 6;f(4) = 6,25$ ${\rm{[}}2;4] \subset (0; + \infty );f(2) = 6,5;f(3) = 6;f(4) = 6,25$

Suy ra: $\mathop {\min }\limits_{{\rm{[}}2;4]} f(x) = f(3) = 6;\mathop {\max }\limits_{{\rm{[}}2;4]} f(x) = f(2) = 6,5$ $\mathop {\min }\limits_{{\rm{[}}2;4]} f(x) = f(3) = 6;\mathop {\max }\limits_{{\rm{[}}2;4]} f(x) = f(2) = 6,5$

Bài 1.24 trang 20 Sách bài tập (SBT) Giải tích 12

Tìm các giá trị của m để phương trình: x³ – 3x² – m = 0 có ba nghiệm phân biệt.

Hướng dẫn làm bài:

Đặt f(x) = x³ – 3x² (C1)

y = m (C2)

Phương trình x³ – 3x² – m = 0 có ba nghiệm phân biệt khi và chỉ khi (C1) và (C2) có ba giao điểm.

Ta có:

$f'(x) = 3{x^2} - 6x = 3x(x - 2) = 0$
$\Leftrightarrow \left[ \matrix{ x = 0 \hfill \cr x = 2 \hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ x = 0 \hfill \cr x = 2 \hfill \cr} \right.$

Bảng biến thiên:

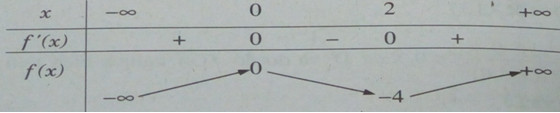
Giải bài tập SBT Toán 12 bài 3

Suy ra (C1),(C2) cắt nhau tại 3 điểm khi -4 < m < 0

Kết luận: Phương trình x³ – 3x² – m = 0 có ba nghiệm phân biệt với những giá trị của m thỏa mãn điều kiện: -4 < m < 0.

Bài 1.25 trang 20 Sách bài tập (SBT) Giải tích 12

Cho số dương m. Hãy phân tích m thành tổng của hai số dương sao cho tích của chúng là lớn nhất.

Hướng dẫn làm bài:

Cho m > 0. Đặt x là số thứ nhất, 0 < x < m, số thứ hai là m – x

Xét tích P(x) = x(m – x)

Ta có: P’(x) = - 2x + m

$P'(x) = 0 < = > x = {m \over 2}$

Bảng biến thiên

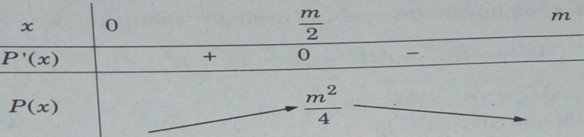
Giải bài tập SBT Toán 12 bài 3

Từ đó ta có giá trị lớn nhất của tích hai số là: $\mathop {\max }\limits_{(0;m)} P(x) = P({m \over 2}) = {{{m^2}} \over 4}$ $\mathop {\max }\limits_{(0;m)} P(x) = P({m \over 2}) = {{{m^2}} \over 4}$

Bài 1.26 trang 20 Sách bài tập (SBT) Giải tích 12

Tìm hai số có hiệu là 13 sao cho tích của chúng là bé nhất.

Hướng dẫn làm bài:

Gọi một trong hai số phải tìm là x, ta có số kia là x + 13

Xét tích:

$p(x) = x(x + 13) = {x^2} + 13x$ $p(x) = x(x + 13) = {x^2} + 13x$

$p'(x) = 2x + 13;p'(x) = 0 < = > x = - {{13} \over 2}$

Bảng biến thiên:

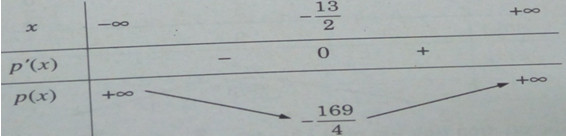
Giải bài tập SBT Toán 12 bài 3

Vậy tích hai số bé nhất khi một số là $\frac{−13}{2}$ $\frac{−13}{2}$ và số kia là $\frac{13}{2}$ $\frac{13}{2}$

Bài 1.27 trang 20 Sách bài tập (SBT) Giải tích 12

Một chất điểm chuyển động theo quy luật s = 6t² – t³. Tính thời điểm t (giây) tại đó vận tốc v (m/s) của chuyển động đạt giá trị lớn nhất.

Hướng dẫn làm bài:

s=6t²−t³,t>0

Vận tốc chuyển động là v = s’ , tức là v = 12t – 3t²

Ta có: v’ = 12 – 6t

v’ = 0 ⇔ t = 2

Hàm số v đồng biến trên khoảng (0;2) và nghịch biến trên khoảng $(2;+∞)$

Vận tốc đạt giá trị lớn nhất khi t = 2. Khi đó $\mathop {\max }\limits_{(0; + \infty )} V = {V_{CD}} = v(2) = 12(m/s)$ $\mathop {\max }\limits_{(0; + \infty )} V = {V_{CD}} = v(2) = 12(m/s)$

Bài 1.28 trang 20 Sách bài tập (SBT) Giải tích 12

Hãy tìm tam giác vuông có diện tích lớn nhất nếu tổng của một cạnh góc vuông và cạnh huyền bằng hằng số a (a > 0).

Hướng dẫn làm bài:

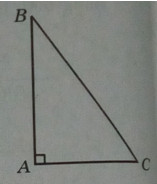
Giải bài tập SBT Toán 12 bài 3

Kí hiệu cạnh góc vuông AB là x, 0<x< $\frac{a}{2}$ $\frac{a}{2}$

Khi đó, cạnh huyền BC = a – x, cạnh góc vuông kia là:

$AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{(a - x)}^2} - {x^2}}$ $AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{(a - x)}^2} - {x^2}}$

Hay $AC = \sqrt {{a^2} - 2ax}$ $AC = \sqrt {{a^2} - 2ax}$

Diện tích tam giác ABC là:

$S(x) = {1 \over 2}x\sqrt {{a^2} - 2ax}$ $S(x) = {1 \over 2}x\sqrt {{a^2} - 2ax}$
$S'(x) = {1 \over 2}\sqrt {{a^2} - 2ax} - {1 \over 2}{{ax} \over {\sqrt {{a^2} - 2ax} }} = {{a(a - 3x)} \over {2\sqrt {{a^2} - 2ax} }}$
$S'(x) = 0 < = > x = {a \over 3}$

Bảng biến thiên:

Giải bài tập SBT Toán 12 bài 3

Tam giác có diện tích lớn nhất khi $AB = {a \over 3};BC = {{2a} \over 3}$ $AB = {a \over 3};BC = {{2a} \over 3}$

---------------------------------

Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải bài tập SBT Toán 12 bài 3. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán lớp 12, Giải bài tập Hóa học lớp 12, Giải bài tập Vật Lí 12 mà VnDoc tổng hợp và đăng tải.