Giải SBT Toán 12 ôn tập chương 3: Nguyên hàm - Tích phân và ứng dụng

Giải SBT Toán lớp 12

Toán 12 - Nguyên hàm - Tích phân và ứng dụng

VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải SBT Toán 12 ôn tập chương 3: Nguyên hàm - Tích phân và ứng dụng, với nội dung tài liệu được tổng hợp chi tiết và chính xác sẽ giúp các bạn học sinh có kết quả cao hơn trong học tập. Mời thầy cô và các bạn học sinh cùng tham khảo.

Giải SBT Toán 12 ôn tập chương 2: Hàm số lũy thừa. Hàm số mũ và hàm số logarit

Giải SBT Toán 12 bài 1: Nguyên hàm

Giải SBT Toán 12 bài 2: Tích phân

Giải SBT Toán 12 bài 3: Ứng dụng hình học của tích phân

Giải SBT Toán 12 ôn tập chương 3

Câu 3.27 trang 185 sách bài tập (SBT) - Giải tích 12

Tính các nguyên hàm sau:

$a) $\int {(2x - 3)\sqrt {x - 3} dx} $$ $a) \(\int {(2x - 3)\sqrt {x - 3} dx} $\), đặt $u = \sqrt {x - 3}$ $\(u = \sqrt {x - 3} $\)

$b) $\int {{x \over {{{(1 + {x^2})}^{{3 \over 2}}}}}} dx$$ $b) \(\int {{x \over {{{(1 + {x^2})}^{{3 \over 2}}}}}} dx$\), đặt $(u = \sqrt {{x^2} + 1})$ $(u = \sqrt {{x^2} + 1})$

$c) $\int {{{{e^x}} \over {{e^x} + {e^{ - x}}}}} dx$$ $c) \(\int {{{{e^x}} \over {{e^x} + {e^{ - x}}}}} dx$\) , đặt $u = {e^{2x}} + 1$ $\(u = {e^{2x}} + 1$\)

$d) $\int {{1 \over {\sin x - \sin a}}} dx$$ $d) \(\int {{1 \over {\sin x - \sin a}}} dx$\)

$e) $\int {\sqrt x \sin \sqrt x } dx$$ $e) \(\int {\sqrt x \sin \sqrt x } dx$\), đặt $t = \sqrt x$ $\(t = \sqrt x $\)

$g)$\int {x\ln {x \over {1 + x}}} dx$$ $g)\(\int {x\ln {x \over {1 + x}}} dx$\)

Hướng dẫn làm bài

$a) ${2 \over 5}{(x - 3)^{{3 \over 2}}}(2x - 1) + C$$ $a) \({2 \over 5}{(x - 3)^{{3 \over 2}}}(2x - 1) + C$\)

$b)$ - {1 \over {\sqrt {1 + {x^2}} }} + C$$ $b)\( - {1 \over {\sqrt {1 + {x^2}} }} + C$\)

$c) ${1 \over 2}\ln ({e^{2x}} + 1) + C$$ $c) \({1 \over 2}\ln ({e^{2x}} + 1) + C$\)

$d) ${1 \over {\cos a}}\ln |{{\sin {{x - a} \over 2}} \over {\cos {{x - a} \over 2}}}| + C$$ $d) \({1 \over {\cos a}}\ln |{{\sin {{x - a} \over 2}} \over {\cos {{x - a} \over 2}}}| + C$\)

HD: Ta có:

$\cos a = \cos ({{x - a} \over 2} - {{x + a} \over 2})$ $\(\cos a = \cos ({{x - a} \over 2} - {{x + a} \over 2})$\)

$e) $ - 2x\cos \sqrt x + 4\sqrt x \sin \sqrt x + 4\cos \sqrt x + C$$ $e) \( - 2x\cos \sqrt x + 4\sqrt x \sin \sqrt x + 4\cos \sqrt x + C$\)

$g) ${{{x^2}} \over 2}\ln {x \over {1 + x}} + {1 \over 2}\ln |1 + x| - {1 \over 2}x + C$$ $g) \({{{x^2}} \over 2}\ln {x \over {1 + x}} + {1 \over 2}\ln |1 + x| - {1 \over 2}x + C$\)

Bài 3.28 trang 186 sách bài tập (SBT) - Giải tích 12

Tính các tích phân sau:

$a) $\int\limits_0^1 {{{(y - 1)}^2}\sqrt y } dy$$ $a) \(\int\limits_0^1 {{{(y - 1)}^2}\sqrt y } dy$\), đặt $t = \sqrt y$ $\(t = \sqrt y $\)

$b) $\int\limits_1^2 {({z^2} + 1)\sqrt[3]{(z-1)^2} } dz$$ $b) \(\int\limits_1^2 {({z^2} + 1)\sqrt[3]{(z-1)^2} } dz$\), đặt $$u = \sqrt[3]{{(z - 1)}^2} )$ \(\(u = \sqrt[3]{{(z - 1)}^2} )$

$c) $\int\limits_1^e {{{\sqrt {4 + 5\ln x} } \over x}} dx$$ $c) \(\int\limits_1^e {{{\sqrt {4 + 5\ln x} } \over x}} dx$\)

$d) $\int\limits_0^{{\pi \over 2}} {({{\cos }^5}\varphi } - {\sin ^5}\varphi )d\varphi $$ $d) \(\int\limits_0^{{\pi \over 2}} {({{\cos }^5}\varphi } - {\sin ^5}\varphi )d\varphi $\)

$e) $\int\limits_0^\pi {{{\cos }^3}\alpha \cos 3\alpha } d\alpha $$ $e) \(\int\limits_0^\pi {{{\cos }^3}\alpha \cos 3\alpha } d\alpha $\)

Hướng dẫn làm bài

$a) ${{16} \over {105}}$$ $a) \({{16} \over {105}}$\)

$b) $2{{49} \over {220}}$$ $b) \(2{{49} \over {220}}$\)

$c) ${{38} \over {15}}$ .$ $c) \({{38} \over {15}}$ .\)

HD: $\int\limits_1^e {{{\sqrt {4 + 5\ln x} } \over x}} dx = {1 \over 5}\int\limits_1^e {{{(4 + 5\ln x)}^{{1 \over 2}}}d(4 + 5\ln x)}$ $\(\int\limits_1^e {{{\sqrt {4 + 5\ln x} } \over x}} dx = {1 \over 5}\int\limits_1^e {{{(4 + 5\ln x)}^{{1 \over 2}}}d(4 + 5\ln x)} $\)

$d) 0$

$e)${\pi \over 8}$ .$ $e)\({\pi \over 8}$ .\)

HD: Dùng công thức hạ bậc đối với ${\cos ^3}x$ $\({\cos ^3}x$\)

Câu 3.29 trang 186 sách bài tập (SBT) - Giải tích 12

Tính các tích phân sau:

$a) $\int\limits_0^{{\pi \over 4}} {\cos 2x} .{\cos ^2}xdx$$ $a) \(\int\limits_0^{{\pi \over 4}} {\cos 2x} .{\cos ^2}xdx$\)

$b) $\int\limits_{{1 \over 2}}^1 {{{{e^x}} \over {{e^{2x}} - 1}}} dx$$ $b) \(\int\limits_{{1 \over 2}}^1 {{{{e^x}} \over {{e^{2x}} - 1}}} dx$\)

$c) $\int\limits_0^1 {{{x + 2} \over {{x^2} + 2x + 1}}} \ln (x + 1)dx$$ $c) \(\int\limits_0^1 {{{x + 2} \over {{x^2} + 2x + 1}}} \ln (x + 1)dx$\)

$d) $\int\limits_0^{{\pi \over 4}} {{{x\sin x + (x + 1)\cos x} \over {x\sin x + \cos x}}} dx$$ $d) \(\int\limits_0^{{\pi \over 4}} {{{x\sin x + (x + 1)\cos x} \over {x\sin x + \cos x}}} dx$\)

Hướng dẫn làm bài

$a) ${1 \over 4}(1 + {\pi \over 4})$ . HD: ${{1 + \cos 2x} \over 2} = {\cos ^2}x$$ $a) \({1 \over 4}(1 + {\pi \over 4})$ . HD: ${{1 + \cos 2x} \over 2} = {\cos ^2}x$\)

$b) ${1 \over 2}\ln {{(e - 1)(\sqrt e + 1)} \over {(e + 1)(\sqrt e - 1)}}$ . HD:${{{e^x}} \over {{e^{2x}} - 1}} = {1 \over 2}({{{e^x}} \over {{e^x} - 1}} - {{{e^x}} \over {{e^x} + 1}})$$ $b) \({1 \over 2}\ln {{(e - 1)(\sqrt e + 1)} \over {(e + 1)(\sqrt e - 1)}}$ . HD:${{{e^x}} \over {{e^{2x}} - 1}} = {1 \over 2}({{{e^x}} \over {{e^x} - 1}} - {{{e^x}} \over {{e^x} + 1}})$\)

$c) ${1 \over 2}({\ln ^2}2 - \ln 2 + 1)$ .$ $c) \({1 \over 2}({\ln ^2}2 - \ln 2 + 1)$ .\)

$HD:${{x + 2} \over {{x^2} + 2x + 1}}\ln (x + 1) = {{\ln (x + 1)} \over {x + 1}} + {{\ln (x + 1)} \over {{{(x + 1)}^2}}}$$ $HD:\({{x + 2} \over {{x^2} + 2x + 1}}\ln (x + 1) = {{\ln (x + 1)} \over {x + 1}} + {{\ln (x + 1)} \over {{{(x + 1)}^2}}}$\)

$d) ${\pi \over 4} + \ln (1 + {\pi \over 4}) - {1 \over 2}\ln 2$ .$ $d) \({\pi \over 4} + \ln (1 + {\pi \over 4}) - {1 \over 2}\ln 2$ .\)

HD: ${{x\sin x + (x + 1)\cos x} \over {x\sin x + \cos x}} = 1 + {{x\cos x} \over {x\sin x + \cos x}}$ $\({{x\sin x + (x + 1)\cos x} \over {x\sin x + \cos x}} = 1 + {{x\cos x} \over {x\sin x + \cos x}}$\) và $d(x\sin x + \cos x) = x\cos xdx$ $\(d(x\sin x + \cos x) = x\cos xdx$\)

Câu 3.30 trang 186 sách bài tập (SBT) - Giải tích 12

Tính diện tich các hình phẳng giới hạn bởi các đường sau:

$a) y = x - 1 + {{\ln x} \over x},y = x - 1$ $a) y = x - 1 + {{\ln x} \over x},y = x - 1$

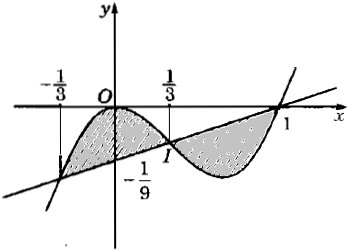
$b)y= x^{3} - x^{2}, y = \frac{1}{9} (x-1)$ $b)y= x^{3} - x^{2}, y = \frac{1}{9} (x-1)$

$c) y = 1 - \sqrt{1-x^2} , y = x^2$ $c) y = 1 - \sqrt{1-x^2} , y = x^2$

Hướng dẫn làm bài

$\left(a\right)\frac{1}{2}$ $\left(a\right)\frac{1}{2}$

$\left(b\right)\frac{8}{81}$ $\left(b\right)\frac{8}{81}$

HD: Đường thẳng $y = \frac{1}{9} (x-1)$ $y = \frac{1}{9} (x-1)$ đi qua tâm đối xứng $I\left(\frac{1}{3};\frac{-2}{27}\right)$ $I\left(\frac{1}{3};\frac{-2}{27}\right)$của hàm số $y = x^3 – x^2.$

Do đó, hình phẳng giới hạn bởi hai đường đã cho gồm hai hình vẽ đối xứng nhau qua điểm I (hình dưới).

Vậy:

$S = 2\int\limits_{ - {1 \over 3}}^{{1 \over 3}} {{\rm{[}}({x^3} - {x^2}) - {1 \over 9}(x - 1){\rm{]}}dx}$ $S = 2\int\limits_{ - {1 \over 3}}^{{1 \over 3}} {{\rm{[}}({x^3} - {x^2}) - {1 \over 9}(x - 1){\rm{]}}dx}$

$= 4\int\limits_0^{{1 \over 3}} {({1 \over 9} - {x^2})dx = {8 \over {81}}}$ $= 4\int\limits_0^{{1 \over 3}} {({1 \over 9} - {x^2})dx = {8 \over {81}}}$

Do theo bài 3.14:

$\int\limits_{ - {1 \over 3}}^{{1 \over 3}} {({x^3} - {1 \over 9}x)dx = 0}$ $\int\limits_{ - {1 \over 3}}^{{1 \over 3}} {({x^3} - {1 \over 9}x)dx = 0}$

Giải SBT Toán 12 ôn tập chương 3: Nguyên hàm - Tích phân và ứng dụng

$\left(c\right)\frac{\pi}{2}-\frac{4}{3}$ $\left(c\right)\frac{\pi}{2}-\frac{4}{3}$

Câu 3.31 trang 186 sách bài tập (SBT) - Giải tích 12

Tính thể tích các khối tròn xoay tạo thành khi quay hình phẳng xác định bởi

$a) y = {x^{{2 \over 3}}},x = 0$ $a) y = {x^{{2 \over 3}}},x = 0$ và tiếp tuyến với đường $y = {x^{{2 \over 3}}}$ $y = {x^{{2 \over 3}}}$ tại điểm có hoành độ x = 1, quanh trục Oy;

$b) y = {1 \over x} - 1,y = 0,y = 2x$ $b) y = {1 \over x} - 1,y = 0,y = 2x$, quanh trục Ox

c) y = |2x – x²|, y = 0 và x = 3 , quanh:

* Trục Ox

* Trục Oy

Hướng dẫn làm bài

$a) {\pi \over {36}}$ $a) {\pi \over {36}}$

Phương trình tiếp tuyến là: $y = {2 \over 3}x + {1 \over 3}$ $y = {2 \over 3}x + {1 \over 3}$

$V = \pi \int\limits_0^1 {{y^3}dy} - \pi \int\limits_{{1 \over 3}}^1 {{{({3 \over 2}y - {1 \over 2})}^2}dy}$ $V = \pi \int\limits_0^1 {{y^3}dy} - \pi \int\limits_{{1 \over 3}}^1 {{{({3 \over 2}y - {1 \over 2})}^2}dy}$

$= {\pi \over 4} - {{2\pi } \over 9}{({3 \over 2}y - {1 \over 2})^3}\left| {\matrix{1 \cr {{1 \over 3}} \cr} = {\pi \over {36}}} \right.$ $= {\pi \over 4} - {{2\pi } \over 9}{({3 \over 2}y - {1 \over 2})^3}\left| {\matrix{1 \cr {{1 \over 3}} \cr} = {\pi \over {36}}} \right.$

$b) \pi ({5 \over 3} - 2\ln 2)$ $b) \pi ({5 \over 3} - 2\ln 2)$

$c) {V_x} = {{18} \over 5}\pi ; {V_y} = {{59} \over 6}\pi$ $c) {V_x} = {{18} \over 5}\pi ; {V_y} = {{59} \over 6}\pi$

${V_y} = \pi {\rm{\{ }}\int\limits_0^1 {{\rm{[(}}1 + \sqrt {1 - y} {)^2} - {{(1 - \sqrt {1 - y} )}^2}{\rm{]}}} dy + \int\limits_0^3 {{\rm{[}}9 - {{(1 + \sqrt {1 + y} )}^2}{\rm{]}}dy\} }$ ${V_y} = \pi {\rm{\{ }}\int\limits_0^1 {{\rm{[(}}1 + \sqrt {1 - y} {)^2} - {{(1 - \sqrt {1 - y} )}^2}{\rm{]}}} dy + \int\limits_0^3 {{\rm{[}}9 - {{(1 + \sqrt {1 + y} )}^2}{\rm{]}}dy\} }$

Câu 3.32 trang 187 sách bài tập (SBT) - Giải tích 12

Hãy chỉ ra các kết quả đúng trong các kết quả sau:

$a) \int\limits_0^1 {{x^n}{{(1 - x)}^m}dx = \int\limits_0^1 {{x^m}{{(1 - x)}^n}} } dx;m,n \in {N^*}$ $a) \int\limits_0^1 {{x^n}{{(1 - x)}^m}dx = \int\limits_0^1 {{x^m}{{(1 - x)}^n}} } dx;m,n \in {N^*}$

$b) \int\limits_{ - 1}^1 {{{{t^2}} \over {{e^t} + 1}}} dt = \int\limits_0^1 {{t^2}dt}$ $b) \int\limits_{ - 1}^1 {{{{t^2}} \over {{e^t} + 1}}} dt = \int\limits_0^1 {{t^2}dt}$

$c) \int\limits_0^1 {{{\sin }^3}x\cos xdx = } \int\limits_0^1 {{t^3}} dt$ $c) \int\limits_0^1 {{{\sin }^3}x\cos xdx = } \int\limits_0^1 {{t^3}} dt$

Hướng dẫn làm bài

a) Đúng

b) Ta có:

$\int\limits_{ - 1}^1 {{{{t^2}dt} \over {{e^t} + 1}}} = \int\limits_{ - 1}^0 {{{{t^2}dt} \over {{e^t} + 1}}} + \int\limits_0^{ - 1} {{{{t^2}dt} \over {{e^t} + 1}}} (*)$ $\int\limits_{ - 1}^1 {{{{t^2}dt} \over {{e^t} + 1}}} = \int\limits_{ - 1}^0 {{{{t^2}dt} \over {{e^t} + 1}}} + \int\limits_0^{ - 1} {{{{t^2}dt} \over {{e^t} + 1}}} (*)$

Dùng phương pháp đổi biến t = - x đối với tích phân $\int\limits_{ - 1}^0 {{{{t^2}dt} \over {{e^t} + 1}}}$ $\int\limits_{ - 1}^0 {{{{t^2}dt} \over {{e^t} + 1}}}$, ta được:

$\int\limits_{ - 1}^0 {{{{t^2}dt} \over {{e^t} + 1}}} = \int\limits_0^1 {{{{x^2}dx} \over {{e^{ - x}} + 1}} = \int\limits_0^1 {{{{t^2}dt} \over {{e^{ - t}} + 1}}} }$ $\int\limits_{ - 1}^0 {{{{t^2}dt} \over {{e^t} + 1}}} = \int\limits_0^1 {{{{x^2}dx} \over {{e^{ - x}} + 1}} = \int\limits_0^1 {{{{t^2}dt} \over {{e^{ - t}} + 1}}} }$

Thay vào (*) ta có:

$\int\limits_{ - 1}^1 {{{{t^2}dt} \over {{e^t} + 1}} = \int\limits_0^1 {{t^2}dt} }$ $\int\limits_{ - 1}^1 {{{{t^2}dt} \over {{e^t} + 1}} = \int\limits_0^1 {{t^2}dt} }$

c) Sai

---------------------------------

Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải SBT Toán 12 ôn tập chương 3: Nguyên hàm - Tích phân và ứng dụng. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán lớp 12, Giải bài tập Hóa học lớp 12, Giải bài tập Vật Lí 12 mà VnDoc tổng hợp và đăng tải.

Chia sẻ, đánh giá bài viết

1

233

Bài trước

Bài sau