Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Đề thi thử vào lớp 10 môn Toán Trường THCS Thị Trấn năm học 2019- 2020

Đề minh họa thi vào 10 năm 2020

Bài trước

Bài sau

Đề thi thử vào lớp 10 môn Toán Trường THCS Thị Trấn năm học 2019- 2020

Đề thi thử vào lớp 10 môn Toán Trường THCS Thị Trấn năm học 2019- 2020. Tài liệu giúp các bạn học sinh củng cố lại phần kiến thức đã học và kỹ năng giải đề thi, biết cách phân bổ thời gian làm bài sao cho hợp lý. Mời các bạn cùng tham khảo

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 9, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 9 sau: Nhóm Tài liệu học tập lớp 9. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Câu 1: (2,0 điểm)

1. Giải phương trình: $x^2+4x+3=0$

2. Giải hệ phương trình: $\left\{ \matrix{ x+y=4 \hfill \cr 3x -2y = 7 \hfill \cr} \right.$ $\left\{ \matrix{ x+y=4 \hfill \cr 3x -2y = 7 \hfill \cr} \right.$

Câu 2: (2,0 điểm)

Cho biểu thức $Q=(\frac{y\sqrt{y}+1}{y-1}-\frac{y-1}{\sqrt{y}-1}):(\sqrt{y}+\frac{\sqrt{y}}{\sqrt{y}-1})$ $Q=(\frac{y\sqrt{y}+1}{y-1}-\frac{y-1}{\sqrt{y}-1}):(\sqrt{y}+\frac{\sqrt{y}}{\sqrt{y}-1})$ với $y>0$ và $y ≠1$

1. Rút gọn $Q$

2. Tính giá trị của $y$ khi $Q=3$

Câu 3: (2,0 điểm)

1. Cho hàm số $y=mx+n (m ≠0)$. Tìm m, n biết đồ thị hàm số song song với đường thẳng

$y=-x+2018$ (d) và đi qua điểm A(1;2018)

2. Tìm n để phương trình $x^2-2(n-1)x-n-5=0$ có 2 nghiệm thoả mãn hệ thức $x_1^2+x_2^2=14$

Câu 4: (3,0 điểm)

Cho đường tròn (O;R), đường kính CD vuông góc với dây cung PQ tại điểm K (K nằm giữa O và D). Trên tia đối của tia QP lấy điểm E nằm ngoài đường tròn (O) sao cho đoạn thẳng CE cắt đường tròn (O) tại điểm H khác C. Hai dây PQ và DH cắt nhau ở M. Qua Q kẻ đường thẳng vuông góc với CE cắt tia PH tại N.

1. Chứng minh tứ giác CKMH nội tiếp

2. Chứng minh tam giác QNH cân và MP.QE = MQ.EP

3. Giả sử HM = HE. Chứng minh OH // PQ

Câu 5: (1,0 điểm)

Cho các số dương a, b, c thoả mãn: $a+b+c=1$

Chứng minh rằng: $\sqrt{2a^2+ab+2b^2}+\sqrt{2b^2+bc+2c^2}+\sqrt{2c^2+ca+2a^2} \geq \sqrt5$ $\sqrt{2a^2+ab+2b^2}+\sqrt{2b^2+bc+2c^2}+\sqrt{2c^2+ca+2a^2} \geq \sqrt5$

Đáp án đề thi thử vào 10 năm 2020 môn Toán - THCS Thị Trấn

Câu 1: (2,0 điểm)

1. Giải phương trình: $x^2+4x+3=0$

$\Leftrightarrow (x+1)(x+3)=0$ $\Leftrightarrow (x+1)(x+3)=0$

$\Leftrightarrow \left[ \matrix{ {x} = {-1} \hfill \cr {x} = {-3} \hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ {x} = {-1} \hfill \cr {x} = {-3} \hfill \cr} \right.$

Vậy phương trình có 2 nghiệm $x=-1$ hoặc $x=-3$

2. Giải hệ phương trình: $\left\{ \matrix{ x+y=4 \hfill \cr 3x -2y = 7 \hfill \cr} \right.$ $\left\{ \matrix{ x+y=4 \hfill \cr 3x -2y = 7 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ 2x+2y=8 \hfill \cr 3x -2y = 7 \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ 2x+2y=8 \hfill \cr 3x -2y = 7 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ 2x+2y=8 \hfill \cr 5x = 15 \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ 2x+2y=8 \hfill \cr 5x = 15 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x=3 \hfill \cr y=1 \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ x=3 \hfill \cr y=1 \hfill \cr} \right.$

Vậy phương trình có 1 nghiệm $(x;y)=(3;1)$

Câu 2: (2,0 điểm)

1. Rút gọn $Q$

Ta có:

$Q=(\frac{y\sqrt{y}+1}{y-1}-\frac{y-1}{\sqrt{y}-1}):(\sqrt{y}+\frac{\sqrt{y}}{\sqrt{y}-1})$ $Q=(\frac{y\sqrt{y}+1}{y-1}-\frac{y-1}{\sqrt{y}-1}):(\sqrt{y}+\frac{\sqrt{y}}{\sqrt{y}-1})$

$\Leftrightarrow Q=(\frac{(\sqrt{y}+1)(y-\sqrt{y}+1)}{(\sqrt{y}-1)(\sqrt{y}+1)}-\frac{y-1}{\sqrt{y}-1}):(\frac{y-\sqrt{y}+\sqrt{y}}{\sqrt{y}-1})$ $\Leftrightarrow Q=(\frac{(\sqrt{y}+1)(y-\sqrt{y}+1)}{(\sqrt{y}-1)(\sqrt{y}+1)}-\frac{y-1}{\sqrt{y}-1}):(\frac{y-\sqrt{y}+\sqrt{y}}{\sqrt{y}-1})$

$\Leftrightarrow Q=(\frac{y-\sqrt{y}+1}{\sqrt{y}-1}-\frac{y-1}{\sqrt{y}-1}):(\frac{y}{\sqrt{y}-1})$ $\Leftrightarrow Q=(\frac{y-\sqrt{y}+1}{\sqrt{y}-1}-\frac{y-1}{\sqrt{y}-1}):(\frac{y}{\sqrt{y}-1})$

$\Leftrightarrow Q=(\frac{y-\sqrt{y}+1-y+1}{\sqrt{y}-1}).(\frac{\sqrt{y}-1}{y})$ $\Leftrightarrow Q=(\frac{y-\sqrt{y}+1-y+1}{\sqrt{y}-1}).(\frac{\sqrt{y}-1}{y})$

$\Leftrightarrow Q=(\frac{2-\sqrt{y}}{\sqrt{y}-1}).(\frac{\sqrt{y}-1}{y})=\frac{2-\sqrt{y}}{y}$ $\Leftrightarrow Q=(\frac{2-\sqrt{y}}{\sqrt{y}-1}).(\frac{\sqrt{y}-1}{y})=\frac{2-\sqrt{y}}{y}$

Vậy $Q=\frac{2-\sqrt{y}}{y}$ $Q=\frac{2-\sqrt{y}}{y}$

2. Tính giá trị của $y$ khi $Q=3$

Khi $Q=3\Leftrightarrow Q=\frac{2-\sqrt{y}}{y} = 3$ $Q=3\Leftrightarrow Q=\frac{2-\sqrt{y}}{y} = 3$

$\Leftrightarrow 3y+\sqrt{y}-2 = 0$ $\Leftrightarrow 3y+\sqrt{y}-2 = 0$

$\Leftrightarrow (\sqrt{y}+1)(3\sqrt{y}-2)=0$ $\Leftrightarrow (\sqrt{y}+1)(3\sqrt{y}-2)=0$

$\Rightarrow \sqrt{y} = -1$ $\Rightarrow \sqrt{y} = -1$ (vô lý) hoặc $\sqrt{y} =\frac{2}{3}\Leftrightarrow y =\frac{4}{9}$ $\sqrt{y} =\frac{2}{3}\Leftrightarrow y =\frac{4}{9}$ (thoả mãn)

Vậy $Q=3\Leftrightarrow y =\frac{4}{9}$ $Q=3\Leftrightarrow y =\frac{4}{9}$

Câu 3: (2,0 điểm)

1. Cho hàm số $y=mx+n (m ≠0)$. Tìm m, n biết đồ thị hàm số song song với đường thẳng

$y=-x+2018$ (d) và đi qua điểm A(1;2018)

Vì đồ thị hàm số đã cho song song với (d) $\Rightarrow m=-1\Rightarrow$ $\Rightarrow m=-1\Rightarrow$ phương trình đồ thị hàm số đã cho có dạng $y=-x+n$

Lại có, đồ thị hàm đã cho đi qua điểm $A(1;2018) \Leftrightarrow 2018=-1+n\Leftrightarrow n=2019$ $A(1;2018) \Leftrightarrow 2018=-1+n\Leftrightarrow n=2019$

Vậy $(m;n)=(-1;2019)$

2. Tìm n để phương trình $x^2-2(n-1)x-n-5=0$ (1) có 2 nghiệm thoả mãn hệ thức $x_1^2+x_2^2=14$

Để phương trình (1) có 2 nghiệm $\Leftrightarrow \Delta$ $\Leftrightarrow \Delta' =(n-1)^2 - (-n-5) \geq 0$

$\Leftrightarrow \Delta$ $\Leftrightarrow \Delta' =n^2-n +6 \geq 0$

Dễ thấy $\Delta$ $\Delta' > 0$ với mọi n nên phương trình đã cho luôn có 2 nghiệm phân biệt.

Áp dụng hệ thức Vi-ét cho (1), ta có:

$\left\{ \matrix{ x_1+x_2=2(n-1) \hfill \cr x_1x_2=-n-5 \hfill \cr} \right. (*)$ $\left\{ \matrix{ x_1+x_2=2(n-1) \hfill \cr x_1x_2=-n-5 \hfill \cr} \right. (*)$

Ta có: $x_1^2+x_2^2=14$

$\Leftrightarrow (x_1+x_2)^2-2x_1x_2=14$ $\Leftrightarrow (x_1+x_2)^2-2x_1x_2=14$

$\Leftrightarrow 4(n-1)^2-2(-n-5)=14$ $\Leftrightarrow 4(n-1)^2-2(-n-5)=14$

$\Leftrightarrow 4n^2-6n+14=14$ $\Leftrightarrow 4n^2-6n+14=14$

$\Leftrightarrow 4n^2-6n=0$ $\Leftrightarrow 4n^2-6n=0$

$\Leftrightarrow \left\{ \matrix{n=0 \hfill \cr n=\frac{3}{2} \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{n=0 \hfill \cr n=\frac{3}{2} \hfill \cr} \right.$

Vậy $n=0$ hoặc $n=\frac{3}{2}$ $n=\frac{3}{2}$ thì $x_1^2+x_2^2=14$

Câu 4: (3,0 điểm)

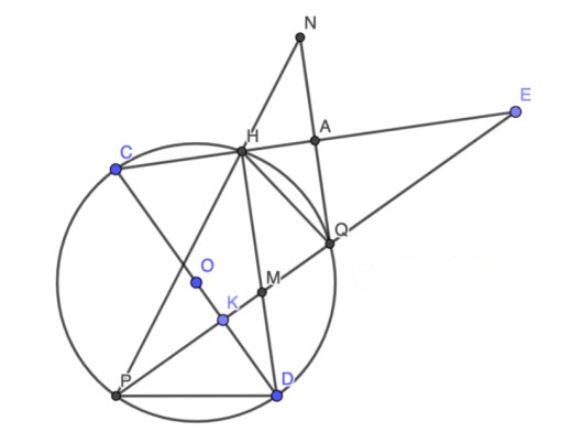
Đề thi thử vào lớp 10 môn Toán Trường THCS Thị Trấn năm học 2019- 2020

1. Chứng minh tứ giác CKMH nội tiếp

Dễ thấy $\angle CKM = \angle CHM = 90⁰$ $\angle CKM = \angle CHM = 90⁰$ (gt) nên tứ giác CKMH nội tiếp (đpcm)

2. Chứng minh tam giác QNH cân và MP.QE = MQ.EP

D là điểm chính giữa cung nhỏ PQ (theo định lý đường kính và dây của đường tròn) => HD là phân giác trong của góc PHQ hay $\angle PHD = \angle QHD$ $\angle PHD = \angle QHD$

Lại có HM // QN (do cùng ⊥ CE) => $\angle PHD = \angle PNQ $ và $\angle QHD = \angle HQN $

Từ 3 điều trên => $\angle HNQ = \angle HQN$ $\angle HNQ = \angle HQN$ => tam giác QNH cân tại H (đpcm)

Xét tam giác PQN có $HM // QN => \frac{PM}{PQ}=\frac{HM}{QN} (1)$ $HM // QN => \frac{PM}{PQ}=\frac{HM}{QN} (1)$

Tương tự với tam giác EHM có $AQ // HM => \frac{EQ}{EM}=\frac{AQ}{HM} (2)$ $AQ // HM => \frac{EQ}{EM}=\frac{AQ}{HM} (2)$

Nhân vế với vế (1) và (2), ta có: $\frac{PM.EQ}{PQ.EM}=\frac{AQ}{QN}=\frac{1}{2}$ $\frac{PM.EQ}{PQ.EM}=\frac{AQ}{QN}=\frac{1}{2}$

$\Leftrightarrow MP.QE=\frac{1}{2}PQ.EM=QK.EM (3)$ $\Leftrightarrow MP.QE=\frac{1}{2}PQ.EM=QK.EM (3)$

Ta có $\triangle MDP \sim \triangle MQH\Rightarrow \frac{MP}{MH}=\frac{MD}{MQ}\Rightarrow MP.MQ = MH.MD$ $\triangle MDP \sim \triangle MQH\Rightarrow \frac{MP}{MH}=\frac{MD}{MQ}\Rightarrow MP.MQ = MH.MD$

$\triangle MKD \sim \triangle MHE\Rightarrow \frac{MK}{MH}=\frac{MD}{ME}\Rightarrow MK.ME = MH.MD$ $\triangle MKD \sim \triangle MHE\Rightarrow \frac{MK}{MH}=\frac{MD}{ME}\Rightarrow MK.ME = MH.MD$

Từ 2 điều trên $\Rightarrow MK.ME = MP.MQ$ $\Rightarrow MK.ME = MP.MQ$

$\Leftrightarrow MK.ME+QM.ME = MP.MQ+QM.ME$ $\Leftrightarrow MK.ME+QM.ME = MP.MQ+QM.ME$

$\Leftrightarrow (MK+QM).ME = MQ.(MP+ME)$ $\Leftrightarrow (MK+QM).ME = MQ.(MP+ME)$

$\Leftrightarrow QK.ME = MQ.EP (4)$ $\Leftrightarrow QK.ME = MQ.EP (4)$

Từ (3) và (4) $\Leftrightarrow MP.QE = MQ.EP (đpcm)$ $\Leftrightarrow MP.QE = MQ.EP (đpcm)$

3. Giả sử HM = HE. Chứng minh OH // PQ

Với HM = HE, ta dễ thấy tam giác MHE vuông cân tại H. Lại có $\triangle MHE \sim \triangle MKD$ $\triangle MHE \sim \triangle MKD$ (2 tam giác vuông có góc đối đỉnh) $\Rightarrow \angle DMK = \angle MDK = 45 ⁰$ $\Rightarrow \angle DMK = \angle MDK = 45 ⁰$ hay $\angle HDC = 45 ⁰$ $\angle HDC = 45 ⁰$ hay tam giác DHC vuông cân tại H. Có HO là trung tuyến của tam giác DHC vuông cân tại $H \Rightarrow HO ⊥ DC$ $H \Rightarrow HO ⊥ DC$

Kết hợp với $PQ ⊥ DC\Rightarrow HO{\space} // {\space}PQ (đpcm)$ $PQ ⊥ DC\Rightarrow HO{\space} // {\space}PQ (đpcm)$

Câu 5: (1,0 điểm)

Cho các số dương a, b, c thoả mãn: $a+b+c=1$

Chứng minh rằng: $\sqrt{2a^2+ab+2b^2}+\sqrt{2b^2+bc+2c^2}+\sqrt{2c^2+ca+2a^2} \geq \sqrt5$ $\sqrt{2a^2+ab+2b^2}+\sqrt{2b^2+bc+2c^2}+\sqrt{2c^2+ca+2a^2} \geq \sqrt5$

Ta đi chứng minh bổ đề:

$2a^2+ab+2b^2 \geq \frac{5}{4}(a+b)^2 (1)$ $2a^2+ab+2b^2 \geq \frac{5}{4}(a+b)^2 (1)$

Thật vậy, (1) $\Leftrightarrow 8a^2+4ab+8b^2 \geq 5(a+b)^2$ $\Leftrightarrow 8a^2+4ab+8b^2 \geq 5(a+b)^2$

$\Leftrightarrow 8a^2+4ab+8b^2 \geq 5a^2+10ab+5b^2$ $\Leftrightarrow 8a^2+4ab+8b^2 \geq 5a^2+10ab+5b^2$

$\Leftrightarrow 3a^2-6ab+3b^2 \geq 0$ $\Leftrightarrow 3a^2-6ab+3b^2 \geq 0$

$\Leftrightarrow 3(a-b)^2 \geq 0$ $\Leftrightarrow 3(a-b)^2 \geq 0$ Luôn đúng với mọi a và b hay ta có đpcm, tức là:

$2a^2+ab+2b^2 \geq \frac{5}{4}(a+b)^2\Leftrightarrow \sqrt{2a^2+ab+2b^2} \geq \frac{\sqrt5}{2}(a+b)$ $2a^2+ab+2b^2 \geq \frac{5}{4}(a+b)^2\Leftrightarrow \sqrt{2a^2+ab+2b^2} \geq \frac{\sqrt5}{2}(a+b)$

Chứng minh tương tự, ta có:

$\sqrt{2b^2+bc+2c^2} \geq \frac{\sqrt5}{2}(b+c)$ $\sqrt{2b^2+bc+2c^2} \geq \frac{\sqrt5}{2}(b+c)$ và

$\sqrt{2c^2+ca+2a^2} \geq \frac{\sqrt5}{2}(c+a)$ $\sqrt{2c^2+ca+2a^2} \geq \frac{\sqrt5}{2}(c+a)$

Cộng vế theo vế các bất đẳng thức trên, ta có:

$\sqrt{2a^2+ab+2b^2}+\sqrt{2b^2+bc+2c^2}+\sqrt{2c^2+ca+2a^2}$ $\sqrt{2a^2+ab+2b^2}+\sqrt{2b^2+bc+2c^2}+\sqrt{2c^2+ca+2a^2}$

$\geq \frac{\sqrt5}{2}[(a+b)+(b+c)+(c+a)] = \sqrt5 (a+b+c) =\sqrt5$ $\geq \frac{\sqrt5}{2}[(a+b)+(b+c)+(c+a)] = \sqrt5 (a+b+c) =\sqrt5$

$\Leftrightarrow \sqrt{2a^2+ab+2b^2}+\sqrt{2b^2+bc+2c^2}+\sqrt{2c^2+ca+2a^2} \geq \sqrt5 (đpcm)$ $\Leftrightarrow \sqrt{2a^2+ab+2b^2}+\sqrt{2b^2+bc+2c^2}+\sqrt{2c^2+ca+2a^2} \geq \sqrt5 (đpcm)$

Dấu bằng xảy ra $\Leftrightarrow a=b=c=\frac{1}{3}$ $\Leftrightarrow a=b=c=\frac{1}{3}$

Đề thi thử vào lớp 10 môn Toán Trường THCS Thị Trấn năm học 2019- 2020 được VnDoc chia sẻ trên đây với 5 câu hỏi tự luận, giúp các bạn học sinh có thêm tài liệu ôn tập chuẩn bị tốt cho kì thi sắp tới. Ngoài đề thi minh họa của trường THCS Thị Trấn các bạn tham khảo các đề của các tỉnh khác nữa nhé

.............................................

Ngoài Đề thi thử vào lớp 10 môn Toán Trường THCS Thị Trấn năm học 2019- 2020. Mời các bạn học sinh còn có thể tham khảo các đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề Thi vào lớp 10 năm 2019 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt