Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Bộ đề thi tuyển sinh lớp 10 môn Toán năm 2020

Đề thi vào lớp 10 môn Toán năm 2020 có đáp án

Bài trước

Bài sau

Đề thi tuyển sinh lớp 10 môn Toán năm 2020

Bộ đề thi tuyển sinh lớp 10 môn Toán năm 2020 được VnDoc sưu tầm và đăng tải. Đây là đề thi vào lớp 10 môn Toán lấy từ các tỉnh trên cả nước cho các bạn đánh giá so sánh đồng thời cũng giúp học sinh làm quen nhiều dạng đề thi tuyển sinh vào lớp 10 khác nhau. Chúc các bạn học tốt, mời các bạn tham khảo

Bộ đề thi tuyển sinh lớp 10 môn Văn năm 2020

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 9, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 9 sau: Nhóm Tài liệu học tập lớp 9. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Đề thi tuyển sinh lớp 10 môn Toán Bình Dương

Sở GD&ĐT Bình Dương

ĐỀ CHÍNH THỨC

KỲ THI TUYỂN SINH VÀO LỚP 10

NĂM HỌC: 2020 - 2021

Môn: Toán

Bài 1 (2,0 điểm). Giải các phương trình, hệ phương trình sau:

$1)\ x^2 + x - 12 = 0$ $1)\ x^2 + x - 12 = 0$

$2 )\ x^4+ 8x^2 - 9 = 0$ $2 )\ x^4+ 8x^2 - 9 = 0$

$3)\ \left\{ \matrix{ 3x + y = -1 \hfill \cr 6x + y = 2 \hfill \cr} \right.$ $3)\ \left\{ \matrix{ 3x + y = -1 \hfill \cr 6x + y = 2 \hfill \cr} \right.$

Bài 2 (1,5 điểm) Cho phương trình: $x^2 – 2020x +2021 = 0$ có hai nghiệm phân biệt.

Không giải phương trình, tính giá trị của các biểu thức sau:

$1)\ \dfrac{1}{x_1} + \dfrac{1}{x_2}$ $1)\ \dfrac{1}{x_1} + \dfrac{1}{x_2}$

$2)\ x_1^2 + x_2^2$ $2)\ x_1^2 + x_2^2$

Bài 3 (1,5 điểm) Cho Parabol (P): $y = \dfrac{3}{2}x^2$ $y = \dfrac{3}{2}x^2$ và đường thẳng (d): $y = -\dfrac{3}{2}x + 3$ $y = -\dfrac{3}{2}x + 3$

1) Vẽ đồ thị của (P) và (d) trên cùng một mặt phẳng tọa độ.

2) Tìm tọa độ các giao điểm của (P) và (d) bằng phép tính.

Bài 4 (1,5 điểm) Cho biểu thức $A = \left( \dfrac{1}{x-\sqrt{x}} + \dfrac{1}{\sqrt{x}-1}\right) : \dfrac{\sqrt{x}+1}{x\sqrt{x}-2x+\sqrt{x}}$ $A = \left( \dfrac{1}{x-\sqrt{x}} + \dfrac{1}{\sqrt{x}-1}\right) : \dfrac{\sqrt{x}+1}{x\sqrt{x}-2x+\sqrt{x}}$

với 0 < x ≠ 1

1) Rút gọn biểu thức A.

2) Tính giá trị của biểu thức A khi

Bài 5 (3,5 điểm) Cho đường tròn (O; 3cm) có đường kính AB và tiếp tuyến Ax. Trên Ax lấy điểm C sao cho AC = 8cm, BC cắt đường tròn (O) tại D. Đường phân giác của các CAD cắt đường tròn (O) tại M và cắt BC tại N.

1) Tính độ dài đoạn thẳng AD.

2) Gọi E là giao điểm của AD và MB. Chứng minh tứ giác MNDE nội tiếp được trong đường tròn.

3) Chứng minh tam giác ABN là tam giác cân.

4) Kẻ EF vuông góc AB (F thuộc AB). Chứng minh: N, E, F thẳng hàng. $x = 8 – 2\sqrt{7}$ $x = 8 – 2\sqrt{7}$

--HẾT--

Đáp án đề tuyển sinh vào lớp 10 môn Toán Bình Dương 2020

Bài 1

$1)\ x^2 + x - 12 = 0$ $1)\ x^2 + x - 12 = 0$

$\begin{array}{l} \Leftrightarrow x^{2}-3 x+4 x-12=0 \\ \Leftrightarrow\left(x^{2}-3 x\right)+(4 x-12)=0 \\ \Leftrightarrow x(x-3)+4(x-3)=0 \\ \Leftrightarrow(x-3)(x+4)=0 \\ \Leftrightarrow\left[\begin{array}{l} x-3=0 \\ x+4=0 \end{array} \Leftrightarrow\left[\begin{array}{l} x=3 \\ x=-4 \end{array}\right.\right. \end{array}$ $\begin{array}{l} \Leftrightarrow x^{2}-3 x+4 x-12=0 \\ \Leftrightarrow\left(x^{2}-3 x\right)+(4 x-12)=0 \\ \Leftrightarrow x(x-3)+4(x-3)=0 \\ \Leftrightarrow(x-3)(x+4)=0 \\ \Leftrightarrow\left[\begin{array}{l} x-3=0 \\ x+4=0 \end{array} \Leftrightarrow\left[\begin{array}{l} x=3 \\ x=-4 \end{array}\right.\right. \end{array}$

Vậy tập nghiệm của phương trình là $S=\{3 ;-4\}$ $S=\{3 ;-4\}$

$2)\ x^4 + 8x^2 - 9 = 0$ $2)\ x^4 + 8x^2 - 9 = 0$

Đặt $t=x^{2}(t \geq 0)$ $t=x^{2}(t \geq 0)$, Phương trình đã cho trở thành: $t^{2}+8 t-9=0$ $t^{2}+8 t-9=0$

Nhận thấy $a+b+c=1+8+(-9)=0$ nên phương trình $t^{2}+8 t-9=0$ $t^{2}+8 t-9=0$ có nghiệm $t=1(t m)$, $t=\frac{c}{a}=-9(k t m)$ $t=\frac{c}{a}=-9(k t m)$

Với t = 1 ta có $x^{2}=1 \Leftrightarrow x=\pm 1$ $x^{2}=1 \Leftrightarrow x=\pm 1$

Vậy tập nghiệm của phương trình là $S=\{\pm 1\}$ $S=\{\pm 1\}$

$\text { 3) }\left\{\begin{array}{l} 3 x+y=-1 \\ 6 x+y=2 \end{array} \Leftrightarrow\left\{\begin{array}{l} 6 x+2 y=-2 \\ 6 x+y=2 \end{array} \Leftrightarrow\left\{\begin{array}{l} y=-4 \\ 3 x+y=-1 \end{array}\right.\right.\right.$ $\text { 3) }\left\{\begin{array}{l} 3 x+y=-1 \\ 6 x+y=2 \end{array} \Leftrightarrow\left\{\begin{array}{l} 6 x+2 y=-2 \\ 6 x+y=2 \end{array} \Leftrightarrow\left\{\begin{array}{l} y=-4 \\ 3 x+y=-1 \end{array}\right.\right.\right.$

$\Leftrightarrow\left\{\begin{array}{l} y=-4 \\ 3 x-4=-1 \end{array} \Leftrightarrow\left\{\begin{array}{l} y=-4 \\ 3 x=3 \end{array} \Leftrightarrow\left\{\begin{array}{l} y=-4 \\ x=1 \end{array}\right.\right.\right.$ $\Leftrightarrow\left\{\begin{array}{l} y=-4 \\ 3 x-4=-1 \end{array} \Leftrightarrow\left\{\begin{array}{l} y=-4 \\ 3 x=3 \end{array} \Leftrightarrow\left\{\begin{array}{l} y=-4 \\ x=1 \end{array}\right.\right.\right.$

Bài 2

Ta có:

$\Delta$ $\Delta' = 1010^2 - 2021 > 0 x1, x2$ tồn tại.

Áp dụng hệ thức Vi-ét ta có:

$\left\{ \matrix{ x_1+x_2 = 2020 \hfill \cr x_1x_2 = 2021 \hfill \cr} \right.$ $\left\{ \matrix{ x_1+x_2 = 2020 \hfill \cr x_1x_2 = 2021 \hfill \cr} \right.$

1) Thay vào ta có:

$\dfrac{1}{x_1} + \dfrac{1}{x_2 } = \dfrac{x_1+x_2}{x_1x_2 } = \dfrac{2020}{2021}$ $\dfrac{1}{x_1} + \dfrac{1}{x_2 } = \dfrac{x_1+x_2}{x_1x_2 } = \dfrac{2020}{2021}$

2) Thay vào ta có:

$x_1^2 + x_2^2 = (x_1+x_2)^2 - 2x_1x_2 = 2020^2 - 2.2021 = 4076358$

Bài 3

Các em nhớ kẻ bảng tọa độ điểm rồi vẽ nhé

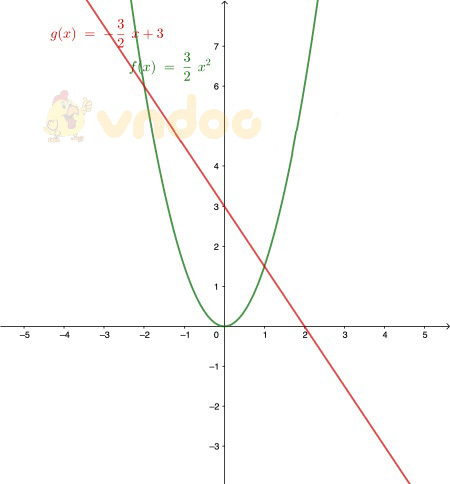
Đáp án đề thi tuyển sinh lớp 10 môn toán năm 2020 Sở GD&ĐT Bình Dương

2. Hoành độ giao điểm của (P) và (d) là:

$\dfrac{3}2 x^2 = -\dfrac{3}2x + 3$ $\dfrac{3}2 x^2 = -\dfrac{3}2x + 3$

$\Leftrightarrow x^2 + x -2 = 0$ $\Leftrightarrow x^2 + x -2 = 0$

$\Leftrightarrow \left[ \matrix{ {x} = 1 \Rightarrow y = \dfrac{3}2 \hfill \cr {x} = -2 \Rightarrow y = 6 \hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ {x} = 1 \Rightarrow y = \dfrac{3}2 \hfill \cr {x} = -2 \Rightarrow y = 6 \hfill \cr} \right.$

KL.....

Bài 4.

1) Với 0 < x ≠ 1 ta có:

$A = \left( \dfrac{1}{x-\sqrt{x}} + \dfrac{1}{\sqrt{x}-1}\right) : \dfrac{\sqrt{x}+1}{x\sqrt{x}-2x+\sqrt{x}}$ $A = \left( \dfrac{1}{x-\sqrt{x}} + \dfrac{1}{\sqrt{x}-1}\right) : \dfrac{\sqrt{x}+1}{x\sqrt{x}-2x+\sqrt{x}}$

$= \dfrac{1+\sqrt{x}}{\sqrt{x}(\sqrt{x}-1)} : \dfrac{\sqrt{x}+1}{\sqrt{x}(\sqrt{x}-1)^2}$ $= \dfrac{1+\sqrt{x}}{\sqrt{x}(\sqrt{x}-1)} : \dfrac{\sqrt{x}+1}{\sqrt{x}(\sqrt{x}-1)^2}$

$= \dfrac{1+\sqrt{x}}{\sqrt{x}(\sqrt{x}-1)} . \dfrac{\sqrt{x}(\sqrt{x}-1)^2}{\sqrt{x}+1}$ $= \dfrac{1+\sqrt{x}}{\sqrt{x}(\sqrt{x}-1)} . \dfrac{\sqrt{x}(\sqrt{x}-1)^2}{\sqrt{x}+1}$

$= \sqrt x -1$ $= \sqrt x -1$

2) Với $x = 8 - 2\sqrt 7 = 7 - 2\sqrt 7 + 1 = (\sqrt 7 -1)^2$ $x = 8 - 2\sqrt 7 = 7 - 2\sqrt 7 + 1 = (\sqrt 7 -1)^2$

Thay vào A ta có:

$A = \sqrt x -1 = \sqrt{(\sqrt 7 -1)^2} - 1 = (\sqrt 7 -1) -1 = \sqrt 7 -2$ $A = \sqrt x -1 = \sqrt{(\sqrt 7 -1)^2} - 1 = (\sqrt 7 -1) -1 = \sqrt 7 -2$

Bài 5:

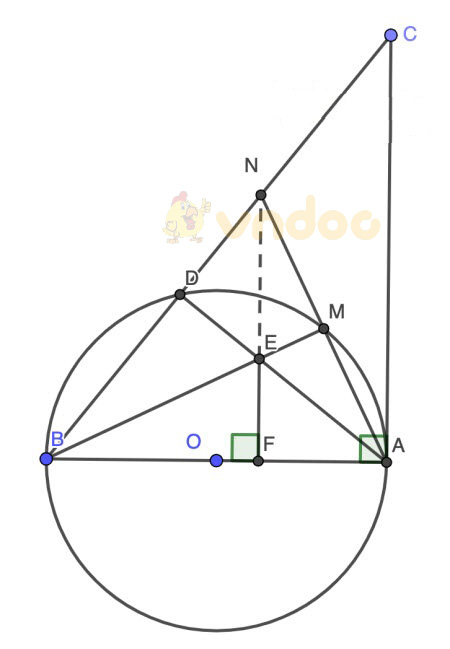
Đáp án đề thi tuyển sinh lớp 10 môn toán năm 2020 Sở GD&ĐT Bình Dương

a) Ta thấy ∠ADB = 90° (góc nội tiếp chắn đường kính AB)

Ta có:

$2 S_{\triangle ABC} = AB. AC = AD.BC$ $2 S_{\triangle ABC} = AB. AC = AD.BC$

$\Rightarrow AD = \dfrac{AB.AC}{BC} = \dfrac{AB.AC}{\sqrt{{AB}^2+{AC}^2}} = \dfrac{6.8}{6^2+8^2}= 4.8 (cm)$ $\Rightarrow AD = \dfrac{AB.AC}{BC} = \dfrac{AB.AC}{\sqrt{{AB}^2+{AC}^2}} = \dfrac{6.8}{6^2+8^2}= 4.8 (cm)$

2) Ta thấy:

∠ADB = ∠AMB = 90° (góc nội tiếp chắn đường kính AB)

Hay ∠NDE = ∠NME = 90° ⇒ D và M cùng thuộc đường tròn đường kính NE, hay tứ giác MNDE nội tiếp (đpcm).

3) Vì AN là phân giác của ∠DAC nên ∠DAN = ∠NAC = 90° - ∠NAB ⇒ ∠NAB = 90° - ∠DAN (1)

Xét △NAD vuông tại D ⇒ ∠DNA + ∠DAN = 90° hay ∠BNA = 90° - ∠DAN (2)

Từ (1) và (2) suy ra ∠NAB = ∠BNA.

Suy ra △NBA cân tại B (đpcm).

Theo giả thiết ta có EF ⊥ AB (*)

Xét △NAB có BM ⊥ AN và AD ⊥ BN (cmt), BM cắt AD tại E ⇒ E là trực tâm của △NAB

Suy ra NE ⊥ AB (**)

Từ (*) và (**) suy ra E, F, N thẳng hàng (đpcm).

Tham khảo thêm: Đáp án đề thi tuyển sinh lớp 10 môn toán năm 2020 Sở GD&ĐT Bình Dương