Đáp án đề thi vào lớp 10 môn Toán tỉnh Nam Định năm 2019
Đề thi vào lớp 10 Toán tỉnh Nam Định năm 2019
Đáp án đề thi vào lớp 10 môn Toán tỉnh Nam Định năm 2019. Tài liệu giúp các bạn học sinh củng cố lại phần kiến thức đã học và kỹ năng giải đề thi, biết cách phân bổ thời gian làm bài sao cho hợp lý. Mời các bạn cùng tham khảo
- Đề thi vào lớp 10 môn Toán tỉnh Tuyên Quang năm 2019
- Đáp án đề thi vào lớp 10 môn Toán tỉnh Thái Bình năm 2019
- Đáp án đề thi vào lớp 10 môn Toán tỉnh Bạc Liêu năm 2019
- Đáp án đề thi vào lớp 10 môn Văn tỉnh Khánh Hòa năm 2019
- Đáp án đề thi vào lớp 10 môn Toán tỉnh Khánh Hòa năm 2019

Gợi ý đáp án đề thi vào lớp 10 môn Toán 2019 Nam Định
Phần I. Trắc nghiệm
1. B
2, A
3. C
4. B
5. D
6. C
7. D
8. A
Phần II. Tự luận
Câu 1

Câu 2

Câu 3

Câu 4

c. Đáp án câu 4c do thầy Leo'class giải đề
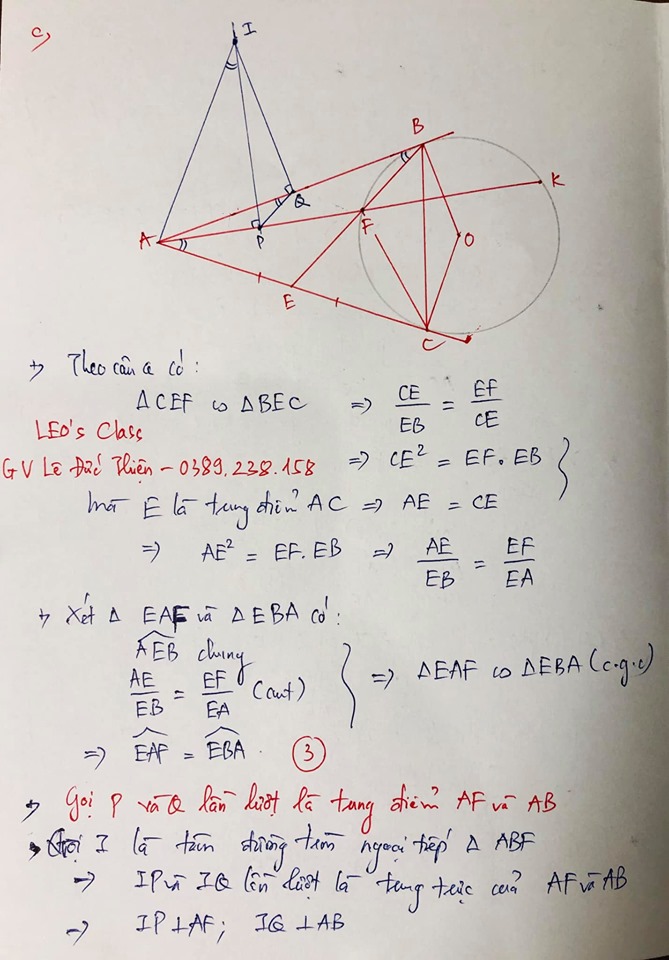

Câu 5
Gợi ý bài cuối:
x³ + y³ + z³ - 3xyz
= (x+y)³ - 3xy(x-y) + z³ - 3xyz
= [(x+y)³ + z³] - 3xy(x+y+z)
= (x+y+z)³ - 3z(x+y)(x+y+z) - 3xy(x-y-z)
= (x+y+z)[(x+y+z)² - 3z(x+y) - 3xy]
= (x+y+z)(x² + y² + z² + 2xy + 2xz + 2yz - 3xz - 3yz - 3xy)
= (x+y+z)(x² + y² + z² - xy - xz - yz)
= (x+y+z) x 1/2[2x² + 2y² + 2z² − 2xy − 2xz − 2yz]
= (x+y+z) x 1/2[(x − y)² + (y − z)² + (z−x)²]
= 2 (theo giả thiết)
Đặt a = x+y+z => a>0
b = x² + y² + z² - xy - xz - yz
=> a.b = 2 => b = 2/a
=> P = 1/2 a² + 4b = 1/2 a² + 4.2/a = 1/2 a² + 8/a
Áp dụng bất đẳng thức Cosi ta có
1/2 a² + 8/a = 1/2 a² + 4/a + 4/a ≥ 3 . 2 = 6
=> Min P ≥ 6 khi a = 2, b = 1
Kết luận: ........
.............................................
Ngoài Đáp án đề thi vào lớp 10 môn Toán tỉnh Nam Định năm 2019. Mời các bạn học sinh còn có thể tham khảo các đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề Thi vào lớp 10 năm 2019 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt









