Đề thi thử vào lớp 10 môn Toán Sở GD&ĐT Thành Phố Hồ Chí Minh năm học 2020 - 2021 - lần 2

Đề thi tuyển sinh vào lớp 10 môn Toán năm 2020 có đáp án

Đề thi thử vào lớp 10 môn Toán Sở GD&ĐT Thành Phố Hồ Chí Minh năm 2020

Đề thi thử vào lớp 10 môn Toán Sở GD&ĐT Thành Phố Hồ Chí Minh năm học 2020 - 2021 - lần 2 được VnDoc sưu tầm và đăng tải. Đây là đề thi tham khảo vào lớp 10 môn Toán dành cho các bạn học sinh ôn tập, củng cố kiến thức, rèn luyện kĩ năng làm bài Toán. Mời các bạn cùng tham khảo

Đề thi thử vào lớp 10 môn Ngữ văn Sở GD&ĐT Thành Phố Hồ Chí Minh năm học 2020 - 2021 - lần 2

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 9, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 9 sau: Nhóm Tài liệu học tập lớp 9. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Đề thi thử vào lớp 10 môn Toán Sở GD&ĐT Thành Phố Hồ Chí Minh năm học 2020 - 2021 - lần 2

Bài 1: (1,5 điểm)

1. Giải phương trình:

$7\sqrt x - 2x +15 = 0$ $7\sqrt x - 2x +15 = 0$

2. Cho parabol $(P): y=a{x}^{2}$ $(P): y=a{x}^{2}$ và đường thẳng $(d_1): -2x+y=4$

a, Viết phương trình đường thẳng $(d_2)$ biết $(d_2)$ song song với $(d_1)$ và đi qua điểm M(1;-1).

b, Tìm giá trị a, biết (P) đi qua N(1;-4). Gọi A, B là giao điểm của (P) và (d_1). Tìm toạ độ trung điểm I của AB. Tính độ dài AB. Hãy biểu diễn đồ thị hàm số (P) vừa tìm được.

Bài 2: (1,0 điểm)

1. Cho phương trình:

$20x^2+5x-2020=0$

Hãy chứng minh phương trình có hai nghiệm phân biệt $x_1;x_2.$ Không giải phương trình trên, hãy tính giá trị của biểu thức sau:

$P = \dfrac{x_1}{x_2}(1-x_2)+ \dfrac{x_2}{x_1}(1-x_1)$ $P = \dfrac{x_1}{x_2}(1-x_2)+ \dfrac{x_2}{x_1}(1-x_1)$

2. Cho phương trình:

$x^2+9x-10 = 0$

Có hai nghiệm phân biệt $x_1;x_2$. Không giải phương trình, hãy lập phương trình bậc hai có hai nghiệm $\dfrac{1}{x_1}$ $\dfrac{1}{x_1}$ và $\dfrac{1}{x_2}$ $\dfrac{1}{x_2}$.

Bài 3: (1,0 điểm)

1. Rút gọn biểu thức sau:

$A = \sqrt{4+\sqrt{15}}+ \sqrt{4-\sqrt{15}} - \sqrt{3-\sqrt{5}}$ $A = \sqrt{4+\sqrt{15}}+ \sqrt{4-\sqrt{15}} - \sqrt{3-\sqrt{5}}$

2. Có một người hỏi Py-ta-go có bao nhiêu học trò. Py-ta-go trả lời: "Một nửa số học trò của tôi học toán, một phần tư học nhạc, một phần bảy đăm chiêu, ngoài ra có ba cô gái". Hỏi số học trò của Py-ta-go là bao nhiêu?

Bài 4: (1,0 điểm)

Có hai hãng điện thoại cố định tính phí gọi cho các thuê bao như sau:

Hãng

Cước thuê bao

(nghìn đồng / tháng)

Cước nội hạt

(nghìn đồng / phút)

A

18

0,22

B

20

0,2

Gọi y (nghìn đồng) là số tiền mà khách hàng cần trả mỗi tháng (y > 0);

Gọi x (phút) là thời gian gọi nội hạt của khách hàng trong mỗi tháng (x ∈ N*)

Biết số tiền mà khách hàng trả mỗi tháng sẽ bao gồm cước thuê bao và cước phí gọi nội hạt trong tháng đó.

a, Hãy biểu diễn y theo x theo từng hãng

b, Hãy cho biết với cách tính phí như trên thì một khách hàng mỗi tháng gọi bình quân trên 4 giờ nên sử dụng mạng của hãng nào sẽ rẻ hơn?

Bài 5: (1,0 điểm)

Cho rằng tỉ trọng người cao tuổi ở Việt Nam được xác định bởi hàm số, trong đó R = 11 + 0,32t tính bằng %, t tính bằng số năm kể từ năm 2011.

a, Hãy tính tỉ trọng người cao tuổi vào năm 2011, 2030 và 2050.

b, Để chuyển từ giai đoạn già hoá dân số (tỉ trọng người cao tuổi chiếm 11%) sang giai đoạn dân số già (tỉ trọng người cao tuổi chiếm 20%) thì Australia mất 73 năm. Hoa Kỳ 69 năm, Canada mất 65 năm. Em hãy tính xem Việt Nam mất khoảng bao nhiêu năm? (làm tròn đến năm)

Tốc độ già hoá của Việt Nam nhanh hay chậm so với các nước trên?

Bài 6: (1,0 điểm)

Một Si-lo chứa dầu do một nhà máy X sản xuất, biết chu vi đáy Si-lo là 50m.

a, Một máy bơm A với hiệu suất làm việc 30 m³/phút. Biết rằng máy bơm mất 30 phút để bơm đầy bể. Tính thể tích của Si-lo đó.

b, Thể tích của khối hình trụ được tính với công thức $V = \dfrac{1}{3}R^2h$ $V = \dfrac{1}{3}R^2h$, trong đó R là bán kính, h là chiều cao. Hãy tính bán kính Si-lo R và chiều cao h (làm tròn đến hàng đơn vị).

Đề thi thử vào 10 môn Toán lần 2 TP Hồ Chí Minh có đáp án chi tiết

Bài 7: (1,0 điểm)

Thường ngày, bạn A đi học từ nhà đến trường với vận tốc 5 km/h thì vừa đúng giờ lên lớp. Nhưng hôm nay, A đi học muộn hơn bình thường 7 phút nên A phải chạy với vận tốc 7,5 km/h và đã đến trường sớm 1 phút. Tính quãng đường từ nhà A đến trường.

Bài 8: (2,5 điểm)

Từ một điểm M nằm ngoài đường tròn tâm O, bán kính R (MO < 2R) vẽ 2 tiếp tuyến MA, MB với (O) (A, B là tiếp điểm). Gọi H là giao điểm của AB và OM.

a, Chứng minh MAOB là tứ giác nội tiếp và H là trung điểm của AB.

b, Gọi E là trung điểm MB. Đoạn AE cắt (O) tại C (khác A), tia MC cắt (O) tại D (khác C). Chứng minh EH song song AM và tứ giác BHCE nội tiếp.

c, Tia BO cắt (O) tại P (khác B). Chứng minh 2 tam giác EMC và EAM đồng dạng, và S_{ABDP} = R.AD (S_{ABDP} là diện tích của tứ giác ABDP).

-Hết-

Đáp án đề thi thử vào lớp 10 môn Toán Sở GD&ĐT Thành Phố Hồ Chí Minh năm 2020

Bài 1: (1,5 điểm)

1.

$7\sqrt x - 2x +15 = 0\ (1)$ $7\sqrt x - 2x +15 = 0\ (1)$

$ĐKXĐ: x \geq 0$ $ĐKXĐ: x \geq 0$

$(1) \Leftrightarrow -2x +7\sqrt{x} + 15 = 0$ $(1) \Leftrightarrow -2x +7\sqrt{x} + 15 = 0$

$\Leftrightarrow \left[ \matrix{ \sqrt x =5 \hfill \cr \sqrt x =-\dfrac{3}{2} \hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ \sqrt x =5 \hfill \cr \sqrt x =-\dfrac{3}{2} \hfill \cr} \right.$

Kết hợp với $ĐKXĐ \Rightarrow x = 25.$ $ĐKXĐ \Rightarrow x = 25.$

2.

a, Vì $(d_2)$ song song với $(d_1)$ và đi qua điểm M(1;-1) nên phương trình đường thẳng $(d_2)$ là:

$-2(x-1)+(y+1)=0$

$\Leftrightarrow -2x +y = -3.$ $\Leftrightarrow -2x +y = -3.$

b, Tìm giá trị a, biết (P) đi qua N(1;-4). Gọi A, B là giao điểm của (P) và $(d_1)$. Tìm toạ độ trung điểm I của AB. Tính độ dài AB. Hãy biểu diễn đồ thị hàm số (P) vừa tìm được.

Vì (P) đi qua N(1;-4) nên ta có:

$-4=a.{1}^{2}$ $-4=a.{1}^{2}$

$\Leftrightarrow a = -4$ $\Leftrightarrow a = -4$

Ta có $(P): y=-4{x}^{2}$ $(P): y=-4{x}^{2}$

$(d_1): -2x+y=4 \Leftrightarrow y = 2x +4$ $(d_1): -2x+y=4 \Leftrightarrow y = 2x +4$

Ta thấy hoành độ giao điểm của (P) và $(d_1)$ là nghiệm của phương trình:

$-4.x^2 = 2x+4$

Ta thấy phương trình trên vô nghiệm nên (P) và $(d_1)$ không cắt nhau $\Rightarrow$ $\Rightarrow$ không tồn tại A và B.

Vẽ đồ thị hàm số (P):

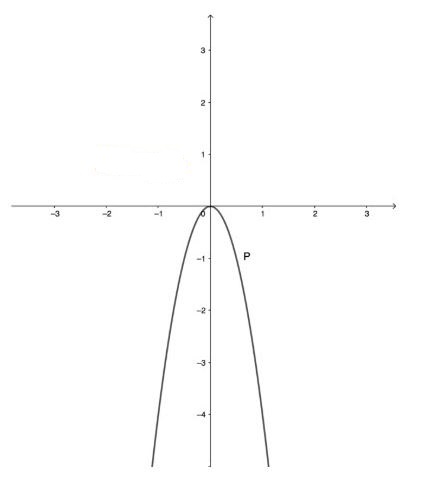
Đề thi thử vào lớp 10 môn Toán Sở GD&ĐT Thành Phố Hồ Chí Minh năm học 2020 - 2021 - lần 2

Bài 2: (1,0 điểm)

1.

+ PT: $20x^2+5x-2020=0 có: \Delta = 5^2 - 4.20.(-2020) = 161625 >0$ $20x^2+5x-2020=0 có: \Delta = 5^2 - 4.20.(-2020) = 161625 >0$

Suy ra phương trình đã cho luôn có hai nghiệm phân biệt $x_1;x_2. ⇒ đpcm$

+ Đề bài cho $P = \dfrac{x_1}{x_2}(1-x_2)+ \dfrac{x_2}{x_1}(1-x_1)$ $P = \dfrac{x_1}{x_2}(1-x_2)+ \dfrac{x_2}{x_1}(1-x_1)$

Áp dụng hệ thức Vi-ét cho phương trình đã cho, ta có:

$\left\{ \matrix{ x_1+x_2 = -\dfrac{5}{20} = -\dfrac{1}{4} \hfill \cr x_1x_2 = -\dfrac{2020}{20} = -101\hfill \cr} \right.$ $\left\{ \matrix{ x_1+x_2 = -\dfrac{5}{20} = -\dfrac{1}{4} \hfill \cr x_1x_2 = -\dfrac{2020}{20} = -101\hfill \cr} \right.$

Dễ thấy phương trình đã cho không có nghiệm x = 0, nên P xác định.

Ta có:

$P = \dfrac{x_1}{x_2}(1-x_2)+ \dfrac{x_2}{x_1}(1-x_1)$ $P = \dfrac{x_1}{x_2}(1-x_2)+ \dfrac{x_2}{x_1}(1-x_1)$

$= \dfrac{x_1}{x_2} - x_1 + \dfrac{x_2}{x_1} - x_2$ $= \dfrac{x_1}{x_2} - x_1 + \dfrac{x_2}{x_1} - x_2$

$= \dfrac{x_1}{x_2} + \dfrac{x_2}{x_1} -( x_1+ x_2)$ $= \dfrac{x_1}{x_2} + \dfrac{x_2}{x_1} -( x_1+ x_2)$

$= \dfrac{x_1^2+x_2^2}{x_1x_2} -( x_1+ x_2)$ $= \dfrac{x_1^2+x_2^2}{x_1x_2} -( x_1+ x_2)$

$= \dfrac{(x_1+x_2)^2-2x_1x_2}{x_1x_2} -( x_1+ x_2)$ $= \dfrac{(x_1+x_2)^2-2x_1x_2}{x_1x_2} -( x_1+ x_2)$

$= \dfrac{(-\dfrac{1}{4} )^2+2.101}{-101} -( -\dfrac{1}{4} ) ≈ -1,75$ $= \dfrac{(-\dfrac{1}{4} )^2+2.101}{-101} -( -\dfrac{1}{4} ) ≈ -1,75$

2. Cho phương trình:

$x^2+9x-10 = 0$

Có hai nghiệm phân biệt $x_1;x_2$. Không giải phương trình, hãy lập phương trình bậc hai có hai nghiệm $\dfrac{1}{x_1}$ $\dfrac{1}{x_1}$ và $\dfrac{1}{x_2}$ $\dfrac{1}{x_2}$.

Ta có:

$\Delta = 9^2 + 4.10 >0$ $\Delta = 9^2 + 4.10 >0$

Suy ra phương trình đã cho luôn có hai nghiệm phân biệt $x_1;x_2$.

Áp dụng hệ thức Vi-ét cho phương trình đã cho, ta có:

$\left\{ \matrix{ x_1+x_2 = -9 \hfill \cr x_1x_2 = -10\hfill \cr} \right.$ $\left\{ \matrix{ x_1+x_2 = -9 \hfill \cr x_1x_2 = -10\hfill \cr} \right.$

Gọi phương trình cần lập là:

$x^2+ax+b= 0$

Để phương trình này có hai nghiệm $\dfrac{1}{x_1}$ $\dfrac{1}{x_1}$ và $\dfrac{1}{x_2}$ $\dfrac{1}{x_2}$, áp dụng hệ thức Vi-ét cho phương trình vừa lập, ta có:

$\left\{ \matrix{ \dfrac{1}{x_1}+\dfrac{1}{x_2}= -a \hfill \cr \dfrac{1}{x_1}.\dfrac{1}{x_2} = b \hfill \cr} \right.$ $\left\{ \matrix{ \dfrac{1}{x_1}+\dfrac{1}{x_2}= -a \hfill \cr \dfrac{1}{x_1}.\dfrac{1}{x_2} = b \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ \dfrac{x_1+x_2}{x_1x_2}= -a \hfill \cr \dfrac{1}{x_1x_2} = b \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ \dfrac{x_1+x_2}{x_1x_2}= -a \hfill \cr \dfrac{1}{x_1x_2} = b \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ \dfrac{-9}{-10}= -a \hfill \cr \dfrac{1}{-10} = b \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ \dfrac{-9}{-10}= -a \hfill \cr \dfrac{1}{-10} = b \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ a = \dfrac{-9}{10} \hfill \cr b = \dfrac{-1}{10} \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ a = \dfrac{-9}{10} \hfill \cr b = \dfrac{-1}{10} \hfill \cr} \right.$

Vậy phương trình cần lập là

$x^2 - \dfrac{9}{10}x - \dfrac{1}{10} = 0$ $x^2 - \dfrac{9}{10}x - \dfrac{1}{10} = 0$

Hay $10x^2 - 9x - 1 = 0$

Bài 3: (1,0 điểm)

1. Ta có:

$A = \sqrt{4+\sqrt{15}}+ \sqrt{4-\sqrt{15}} - \sqrt{3-\sqrt{5}}$ $A = \sqrt{4+\sqrt{15}}+ \sqrt{4-\sqrt{15}} - \sqrt{3-\sqrt{5}}$

$=\dfrac{1}{\sqrt2} (\sqrt{8+2\sqrt{15}}+ \sqrt{8-2\sqrt{15}} - \sqrt{6-2\sqrt{5}})$ $=\dfrac{1}{\sqrt2} (\sqrt{8+2\sqrt{15}}+ \sqrt{8-2\sqrt{15}} - \sqrt{6-2\sqrt{5}})$

$=\dfrac{1}{\sqrt2} (\sqrt{5+2\sqrt{5.3}+3}+ \sqrt{5-2\sqrt{5.3}+3} - \sqrt{5-2\sqrt{5.1}+1})$ $=\dfrac{1}{\sqrt2} (\sqrt{5+2\sqrt{5.3}+3}+ \sqrt{5-2\sqrt{5.3}+3} - \sqrt{5-2\sqrt{5.1}+1})$

$=\dfrac{1}{\sqrt2} (\sqrt{(\sqrt{5}+\sqrt{3})^2}+ \sqrt{(\sqrt{5}-\sqrt{3})^2} - \sqrt{(\sqrt{5}-1)^2})$ $=\dfrac{1}{\sqrt2} (\sqrt{(\sqrt{5}+\sqrt{3})^2}+ \sqrt{(\sqrt{5}-\sqrt{3})^2} - \sqrt{(\sqrt{5}-1)^2})$

$=\dfrac{1}{\sqrt2} [\sqrt{5}+\sqrt{3}+ \sqrt{5}-\sqrt{3} - (\sqrt{5}-1)]$ $=\dfrac{1}{\sqrt2} [\sqrt{5}+\sqrt{3}+ \sqrt{5}-\sqrt{3} - (\sqrt{5}-1)]$

$=\dfrac{\sqrt{5}+1}{\sqrt2}$ $=\dfrac{\sqrt{5}+1}{\sqrt2}$

2.

Gọi số học trò của Py-ta-go là x (x ∈ N*)

Số học trò học toán là: $\dfrac{x}{2}$ $\dfrac{x}{2}$

Số học trò học nhạc là: $\dfrac{x}{4}$ $\dfrac{x}{4}$

Số học trò đăm chiêu là: $\dfrac{x}{7}$ $\dfrac{x}{7}$

Theo giả thiết ta có:

$x = \dfrac{x}{2} + \dfrac{x}{4} + \dfrac{x}{7} + 3$ $x = \dfrac{x}{2} + \dfrac{x}{4} + \dfrac{x}{7} + 3$

$\Leftrightarrow x = 28$ $\Leftrightarrow x = 28$

Bài 4: (1,0 điểm)

Có hai hãng điện thoại cố định tính phí gọi cho các thuê bao như sau:

Hãng

Cước thuê bao

(nghìn đồng / tháng)

Cước nội hạt

(nghìn đồng / phút)

A

18

0,22

B

20

0,2

Gọi y (nghìn đồng) là số tiền mà khách hàng cần trả mỗi tháng (y > 0);

Gọi x (phút) là thời gian gọi nội hạt của khách hàng trong mỗi tháng (x ∈ N*)

Biết số tiền mà khách hàng trả mỗi tháng sẽ bao gồm cước thuê bao và cước phí gọi nội hạt trong tháng đó.

a, Hãy biểu diễn y theo x theo từng hãng

Ta có:

Hãng A: y = 18 + 0,22x

Hãng B: y = 20 + 0,2x

b, Hãy cho biết với cách tính phí như trên thì một khách hàng mỗi tháng gọi bình quân trên 4 giờ nên sử dụng mạng của hãng nào sẽ rẻ hơn?

Đổi 4 giờ = 240 phút.

Số tiền nếu sử dụng hãng A - số tiền nếu sử dụng hãng B là:

$M= 18 + 0,22x - 20 - 0,2x = 0,02x - 2$

Ta thấy với x > 240 phút

$\Rightarrow M = 0,02 x - 2 > 0,02 \times 240 - 2 = 2,8 >0$ $\Rightarrow M = 0,02 x - 2 > 0,02 \times 240 - 2 = 2,8 >0$

Vậy nếu khách dùng bình quân trên 4 giờ thì M > 0, hay số tiền sử dụng của hãng B sẽ nhỏ hơn.

Vậy khách hàng mỗi tháng gọi bình quân trên 4 giờ nên sử dụng mạng của hãng B sẽ rẻ hơn.

Bài 5: (1,0 điểm)

Cho rằng tỉ trọng người cao tuổi ở Việt Nam được xác định bởi hàm số, trong đó R = 11 + 0,32t tính bằng %, t tính bằng số năm kể từ năm 2011.

a,

Tỉ trọng người cao tuổi vào năm 2011:

$R_{2011} = 11 + 0,32.(2011-2011) = 11$ $R_{2011} = 11 + 0,32.(2011-2011) = 11$ $(\%)$ $(\%)$

Tỉ trọng người cao tuổi vào năm 2030:

$R_{2030} = 11 + 0,32.(2030-2011)=17,08$ $R_{2030} = 11 + 0,32.(2030-2011)=17,08$ $(\%)$ $(\%)$

Tỉ trọng người cao tuổi vào năm 2050:

$R_{2050} = 11 + 0,32.(2050-2011)=23,48$ $R_{2050} = 11 + 0,32.(2050-2011)=23,48$ $(\%)$ $(\%)$

b, Để chuyển từ giai đoạn già hoá dân số (tỉ trọng người cao tuổi chiếm 11%) sang giai đoạn dân số già (tỉ trọng người cao tuổi chiếm 20%) thì Australia mất 73 năm. Hoa Kỳ 69 năm, Canada mất 65 năm. Em hãy tính xem Việt Nam mất khoảng bao nhiêu năm? (làm tròn đến năm)

Với t = 0, Việt Nam có R = 11 %

Để chuyển sang giai đoạn dân số già suy ra:

R = 11 + 0,32t = 20 (%)

$\Leftrightarrow t = 28,125$ $\Leftrightarrow t = 28,125$ (năm)

Ta thấy tốc độ già hoá của Việt Nam nhanh hơn các nước trên.

Việt Nam mất hơn 28 năm để chuyển từ giai đoạn già hoá dân số (tỉ trọng người cao tuổi chiếm 11%) sang giai đoạn dân số già (tỉ trọng người cao tuổi chiếm 20%).

Bài 6: (1,0 điểm)

a,

Thể tích của Si-lo là:

$V = 30 \times 3 = 90 \space (m^3)$ $V = 30 \times 3 = 90 \space (m^3)$

b,

Ta có chu vi đáy là:

$P =2 \pi R = 50$ $P =2 \pi R = 50$

$\Leftrightarrow R ≈ 8 (m)$ $\Leftrightarrow R ≈ 8 (m)$

Thể tích là:

$V = \dfrac{1}{3}R^2h = 90 (m^3)$ $V = \dfrac{1}{3}R^2h = 90 (m^3)$

$\Leftrightarrow h ≈ 4 (m)$ $\Leftrightarrow h ≈ 4 (m)$

Bài 7: (1,0 điểm)

Thường ngày, bạn A đi học từ nhà đến trường với vận tốc 5 km/h thì vừa đúng giờ lên lớp. Nhưng hôm nay, A đi học muộn hơn bình thường 7 phút nên A phải chạy với vận tốc 7,5 km/h và đã đến trường sớm 1 phút. Tính quãng đường từ nhà A đến trường.

Gọi quãng đường từ nhà A đến trường là s (km) (s > 0).

Thời gian hàng ngày A tới trường là: $\dfrac{s}{5} (h)$ $\dfrac{s}{5} (h)$

Theo giả thiết ta có:

$\dfrac{s}{5} = \dfrac{s}{7,5} +\dfrac{7+1}{60}$ $\dfrac{s}{5} = \dfrac{s}{7,5} +\dfrac{7+1}{60}$

$\Leftrightarrow s = 2 (km)$ $\Leftrightarrow s = 2 (km)$

Bài 8: (2,5 điểm)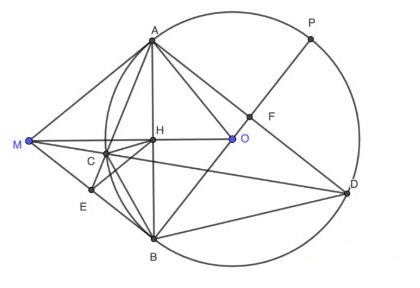
Đề thi thử vào lớp 10 môn Toán Sở GD&ĐT Thành Phố Hồ Chí Minh năm học 2020 - 2021 - lần 2

a,

Vì MA và MB là tiếp tuyến tới (O), A và B lần lượt là tiếp điểm nên MA ⊥ OA và MB ⊥ OB hay ∠MAO = ∠MBO = 90⁰.

Suy ra tứ giác MAOB nội tiếp đường tròn đường kính OM (đpcm)

Theo tính chất của tiếp tuyến, ta có MO vuông góc với AB tại H, đồng thời H là trung điểm của AB (đpcm)

b,

Xét tam giác BAM, có E là trung điểm MB (gt), H là trung điểm AB (cmt) suy ra EH là đường trung bình của tam giác BAM hay EH // AM (đpcm).

Ta có $∠CBA = \frac{1}{2}∠COA = \frac{1}{2}(180⁰ - 2.∠CAO) = 90⁰ - ∠CAO = ∠MAC.$ $∠CBA = \frac{1}{2}∠COA = \frac{1}{2}(180⁰ - 2.∠CAO) = 90⁰ - ∠CAO = ∠MAC.$

Lại có $EH // AM (cmt) \Rightarrow ∠MAC = ∠CEH$ $EH // AM (cmt) \Rightarrow ∠MAC = ∠CEH$

Hay ∠CBA = ∠CEH (cùng = ∠MAC) suy ra tứ giác BHCE nội tiếp (tính chất góc nội tiếp cùng chắn cung CH) (đpcm)

c,

Xét tam giác ECB và EBA, có:

Góc AEB chung

∠EBC = ∠CAB (tính chất góc tạo bởi tiếp tuyến EB và dây cung BC)

Suy ra $△ECB ∽ △EBA \Rightarrow \dfrac{EB}{EC} =\dfrac{EA}{EB} \Rightarrow \dfrac{EM}{EC} =\dfrac{EA}{EM}$ $△ECB ∽ △EBA \Rightarrow \dfrac{EB}{EC} =\dfrac{EA}{EB} \Rightarrow \dfrac{EM}{EC} =\dfrac{EA}{EM}$ (do E là trung điểm MB hay ME = EB)

Xét

tam giác EMC và EAM, có:

Góc MEC chung

$\dfrac{EM}{EC} =\dfrac{EA}{EM}$ $\dfrac{EM}{EC} =\dfrac{EA}{EM}$

Suy ra $△EMC ∽ △EAM (đpcm)$

Ta có $∠EBA = ∠BDA$ (tính chất góc tạo bởi tiếp tuyến EB và dây cung BA)

Vì tứ giác ECHB nội tiếp (cmt) $\Rightarrow ∠ECB = ∠EHB$ $\Rightarrow ∠ECB = ∠EHB$ (góc nội tiếp cùng chắn cung EB)

Ta có EH // MA (cmt) $\Rightarrow ∠AMB = ∠HEB$ $\Rightarrow ∠AMB = ∠HEB$

Cộng vế theo vế 2 biểu thức trên, ta có:

$∠ECB + ∠AMB = ∠EHB + ∠HEB = 180⁰ - ∠EBA$

$\Rightarrow ∠EBA = 180⁰ - ∠ECB - ∠AMB\ (1)$ $\Rightarrow ∠EBA = 180⁰ - ∠ECB - ∠AMB\ (1)$

Lại có $△EMC ∽ △EAM (cmt) \Rightarrow ∠AMB = ∠MCE$ $△EMC ∽ △EAM (cmt) \Rightarrow ∠AMB = ∠MCE$, thay vào (1), ta có:

$∠BDA = ∠EBA = 180⁰ - ∠ECB - ∠MCE = ∠BCD = ∠BAD$ (góc nội tiếp (O) cùng chắn cung BD)

$\Rightarrow △BAD$ $\Rightarrow △BAD$ cân tại $B \Rightarrow AB = BD$ $B \Rightarrow AB = BD$.

Dễ chứng minh $△BAP = △BDP (c.g.c) \Rightarrow ∠ABP = ∠PBD$ $△BAP = △BDP (c.g.c) \Rightarrow ∠ABP = ∠PBD$ hay BP là tia phân giác của ABD.

$△BAD$ cân tại B có BP là phân giác góc B hay BP cũng đồng thời vuông góc với AD hay BP ⊥ AD.

Gọi AD cắt BP tại F, ta có:

$S_{ABDP} = S_{BAP} + S_{BDP}$ $S_{ABDP} = S_{BAP} + S_{BDP}$

$=\dfrac{1}{2} AF.BP + \dfrac{1}{2}FD.BP$ $=\dfrac{1}{2} AF.BP + \dfrac{1}{2}FD.BP$

$=\dfrac{1}{2} BP (AF+ FD)$ $=\dfrac{1}{2} BP (AF+ FD)$

$=\dfrac{1}{2} BP .AD$ $=\dfrac{1}{2} BP .AD$

$=R .AD$

Hay $S_{ABDP} = R.AD (đpcm)$ $S_{ABDP} = R.AD (đpcm)$

Đề thi thử vào lớp 10 môn Toán Sở GD&ĐT Thành Phố Hồ Chí Minh năm học 2020 - 2021 - lần 2 được VnDoc chia sẻ trên đây với 8 câu hỏi với thời gian 120 phút, giúp các bạn học sinh có thêm tài liệu ôn tập chuẩn bị tốt cho kì thi sắp tới. Ngoài đề thi minh thử của TPHCM các bạn tham khảo các đề của các tỉnh khác nữa nhé

.............................................

Ngoài Đề thi thử vào lớp 10 môn Toán Sở GD&ĐT Thành Phố Hồ Chí Minh năm học 2020 - 2021 - lần 2. Mời các bạn học sinh còn có thể tham khảo các đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề Thi vào lớp 10 năm 2019 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt

Chia sẻ, đánh giá bài viết

2

14.883

Bài trước

Bài sau