Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Đề thi thử vào lớp 10 môn Toán Chung Trường THPT Chuyên KHTN, Hà Nội năm 2020 (lần 2)

Đề tuyển sinh vào 10 môn Toán năm 2020 có đáp án

Bài trước

Bài sau

Đề thi thử vào lớp 10 môn Toán Chung Trường THPT Chuyên KHTN năm 2020 (lần 2)

Thư viện đề thi VnDoc Đề thi thử vào lớp 10 môn Toán Chung Trường THPT Chuyên KHTN, Hà Nội năm 2020 (lần 2). Đề thi vào lớp 10 môn Toán này sẽ giúp các bạn học sinh tự ôn luyện và hệ thống lại kiến thức, chuẩn bị tốt cho ôn thi vào lớp 10 các trường THPT sắp tới. Mời các bạn tham khảo.

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 9, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 9 sau: Nhóm Tài liệu học tập lớp 9. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

ĐẠI HỌC QUỐC GIA HÀ NỘI

TRƯỜNG ĐẠI HỌC KHOA HỌC TỰ NHIÊN

ĐỀ KIỂM TRA KIẾN THỨC LẦN 2

TRƯỜNG THPT CHUYÊN KHTN

NĂM HỌC 2019 - 2020

MÔN: Toán LỚP 9

Thời gian làm bài: 120 phút (Không kể thời gian phát đề)

Câu I (3 điểm)

1) Giải phương trình

$3\sqrt{x+3} + 2x\sqrt{x^2-3x+9} = 6x + \sqrt{x^3+27}$ $3\sqrt{x+3} + 2x\sqrt{x^2-3x+9} = 6x + \sqrt{x^3+27}$

2) Giải hệ phương trình

$\left\{ \matrix{ x^2 + y^2 = 2 \hfill \cr (x+y)(x^4+y^4 + 6x^2y^2 + 8xy) = 32 \hfill \cr} \right.$ $\left\{ \matrix{ x^2 + y^2 = 2 \hfill \cr (x+y)(x^4+y^4 + 6x^2y^2 + 8xy) = 32 \hfill \cr} \right.$

Câu II (3 điểm)

1) Tìm x, y nguyên thoả mãn

$(x+y+1)^3 = 7 + x^3 + y^3$

2) Với x, y, z > 0 thoả mãn x + y + z = 3, tìm giá trị lớn nhất của biểu thức

$P = \dfrac{x}{3x+yz} + \dfrac{y}{3y+zx} + \dfrac{z}{3z+xy}$ $P = \dfrac{x}{3x+yz} + \dfrac{y}{3y+zx} + \dfrac{z}{3z+xy}$

Câu III (3 điểm) Cho hình thoi ABCD với ∠BAD < 90°. Đường tròn (I) nội tiếp tam giác ABD tiếp xúc với BD, BA theo thứ tự tại các điểm J, L. Trên đường thẳng LJ lấy điểm K sao cho BK song song với ID.

1) Chứng minh rằng KB vuông góc với KC.

2) Chứng minh rằng bốn điểm L, C, K, I cùng nằm trên một đường tròn.

3) Chứng minh rằng diện tích hình thoi ABCD gấp 8 lần diện tích tam giác BJK.

Câu IV (1 điểm) Với a,b,c\geq 0, không đồng thời bằng 0. Chứng minh rằng

$\sqrt[3]{\dfrac{a}{b+c}} + \sqrt[3]{\dfrac{b}{c+a}} + \sqrt[3]{\dfrac{c}{a+b}} \geq 2$ $\sqrt[3]{\dfrac{a}{b+c}} + \sqrt[3]{\dfrac{b}{c+a}} + \sqrt[3]{\dfrac{c}{a+b}} \geq 2$

Hết

Đáp án đề thi thử vào lớp 10 môn Toán Trường THPT Chuyên KHTN năm 2020

Câu I:

$1)\ 3\sqrt{x+3} + 2x\sqrt{x^2-3x+9} = 6x + \sqrt{x^3+27}$ $1)\ 3\sqrt{x+3} + 2x\sqrt{x^2-3x+9} = 6x + \sqrt{x^3+27}$

$ĐKXĐ: x\geq -3$ $ĐKXĐ: x\geq -3$

$\Leftrightarrow 3\sqrt{x+3} + 2x\sqrt{x^2-3x+9} = 6x + \sqrt{(x+3)(x^2-3x+9)}$ $\Leftrightarrow 3\sqrt{x+3} + 2x\sqrt{x^2-3x+9} = 6x + \sqrt{(x+3)(x^2-3x+9)}$

$\Leftrightarrow \sqrt{x+3}(3 - \sqrt{x^2-3x+9}) - 2x(3 -\sqrt{x^2-3x+9} ) = 0$ $\Leftrightarrow \sqrt{x+3}(3 - \sqrt{x^2-3x+9}) - 2x(3 -\sqrt{x^2-3x+9} ) = 0$

$\Leftrightarrow (\sqrt{x+3}- 2x)(3 - \sqrt{x^2-3x+9})= 0$ $\Leftrightarrow (\sqrt{x+3}- 2x)(3 - \sqrt{x^2-3x+9})= 0$

$\Leftrightarrow \left[ \matrix{ 2x =\sqrt{x+3} \hfill \cr \sqrt{x^2-3x+9} = 3 \hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ 2x =\sqrt{x+3} \hfill \cr \sqrt{x^2-3x+9} = 3 \hfill \cr} \right.$

$\Leftrightarrow \left[ \matrix{ 4x^2 =x+3 \hfill \cr {x^2-3x+9} = 9 \hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ 4x^2 =x+3 \hfill \cr {x^2-3x+9} = 9 \hfill \cr} \right.$

$\Leftrightarrow \left[ \matrix{ x =1 \hfill \cr x =\dfrac{-3}{4} \hfill \cr x =3 \hfill \cr x = 0 \hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ x =1 \hfill \cr x =\dfrac{-3}{4} \hfill \cr x =3 \hfill \cr x = 0 \hfill \cr} \right.$ (thoả mãn đkxđ)

KL.....

$\Leftrightarrow \left\{ \matrix{ (x+y)^2 - 2xy = 2 \hfill \cr (x+y)[(x^2+y^2)^2 + 4x^2y^2 + 8xy] = 32 \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ (x+y)^2 - 2xy = 2 \hfill \cr (x+y)[(x^2+y^2)^2 + 4x^2y^2 + 8xy] = 32 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ xy = \dfrac{(x+y)^2}2 - 1 \hfill \cr (x+y)\left[4 + 4\left(\dfrac{(x+y)^2}2 - 1 \right)^2 + 8\left(\dfrac{(x+y)^2}2 - 1 \right)\right] = 32 \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ xy = \dfrac{(x+y)^2}2 - 1 \hfill \cr (x+y)\left[4 + 4\left(\dfrac{(x+y)^2}2 - 1 \right)^2 + 8\left(\dfrac{(x+y)^2}2 - 1 \right)\right] = 32 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ xy = \dfrac{(x+y)^2}2 - 1 \hfill \cr (x+y)(x+y)^4= 32 \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ xy = \dfrac{(x+y)^2}2 - 1 \hfill \cr (x+y)(x+y)^4= 32 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ xy = \dfrac{(x+y)^2}2 - 1 = 1\hfill \cr x+y = 2 \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ xy = \dfrac{(x+y)^2}2 - 1 = 1\hfill \cr x+y = 2 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x = 1\hfill \cr y = 1 \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ x = 1\hfill \cr y = 1 \hfill \cr} \right.$

KL.....

Câu II:

$(x+y+1)^3 = 7 + x^3 + y^3$

$\Leftrightarrow (x+y)^3 + 1 + 3(x+y)^2 + 3(x+y) = 7 + (x+y)(x^2-xy+y^2)$ $\Leftrightarrow (x+y)^3 + 1 + 3(x+y)^2 + 3(x+y) = 7 + (x+y)(x^2-xy+y^2)$

$\Leftrightarrow(x+y)[ (x+y)^2 + 3(x+y) + 3 -(x^2-xy+y^2) ] = 6$ $\Leftrightarrow(x+y)[ (x+y)^2 + 3(x+y) + 3 -(x^2-xy+y^2) ] = 6$

$\Leftrightarrow(x+y)[ 3xy+ 3(x+y) + 3] = 6$ $\Leftrightarrow(x+y)[ 3xy+ 3(x+y) + 3] = 6$

$\Leftrightarrow(x+y)(xy+ x+y + 1) = 2 =1.2 = (-1).(-2)$ $\Leftrightarrow(x+y)(xy+ x+y + 1) = 2 =1.2 = (-1).(-2)$

$\Leftrightarrow \left[ \matrix{ x+y = 1 \Rightarrow xy+x+y+1 = 2 \Rightarrow xy =0 \hfill \cr x+y = -1 \Rightarrow xy+x+y+1 = -2 \Rightarrow xy =-2 \hfill \cr x+y = 2 \Rightarrow xy+x+y+1 = 1 \Rightarrow xy =-2 \hfill \cr x+y = -2 \Rightarrow xy+x+y+1 = -1 \Rightarrow xy =0 \hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ x+y = 1 \Rightarrow xy+x+y+1 = 2 \Rightarrow xy =0 \hfill \cr x+y = -1 \Rightarrow xy+x+y+1 = -2 \Rightarrow xy =-2 \hfill \cr x+y = 2 \Rightarrow xy+x+y+1 = 1 \Rightarrow xy =-2 \hfill \cr x+y = -2 \Rightarrow xy+x+y+1 = -1 \Rightarrow xy =0 \hfill \cr} \right.$

$\Leftrightarrow \left[ \matrix{ (x;y) = (1;0) \space ∨ \space (x;y) = (0;1) \hfill \cr (x;y) = (1;-2) \space ∨ \space (x;y) = (-2;1) \hfill \cr (x;y) = (1+\sqrt 3;1-\sqrt 3) \space ∨ \space (x;y) = (1-\sqrt 3;1+\sqrt 3) \hfill \cr (x;y) = (0;-2) \space ∨ \space (x;y) = (-2;0) \hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ (x;y) = (1;0) \space ∨ \space (x;y) = (0;1) \hfill \cr (x;y) = (1;-2) \space ∨ \space (x;y) = (-2;1) \hfill \cr (x;y) = (1+\sqrt 3;1-\sqrt 3) \space ∨ \space (x;y) = (1-\sqrt 3;1+\sqrt 3) \hfill \cr (x;y) = (0;-2) \space ∨ \space (x;y) = (-2;0) \hfill \cr} \right.$

Loại bộ nghiệm không nguyên, ta có kết luận: phương trình đã cho có 6 bộ nghiệm....

$P = \dfrac{x}{3x+yz} + \dfrac{y}{3y+zx} + \dfrac{z}{3z+xy}$ $P = \dfrac{x}{3x+yz} + \dfrac{y}{3y+zx} + \dfrac{z}{3z+xy}$

$= \dfrac{x}{(x+y+z)x+yz} + \dfrac{y}{(x+y+z)y+zx} + \dfrac{z}{(x+y+z)z+xy}$ $= \dfrac{x}{(x+y+z)x+yz} + \dfrac{y}{(x+y+z)y+zx} + \dfrac{z}{(x+y+z)z+xy}$

$= \dfrac{x}{(x+y)(x+z)} + \dfrac{y}{(y+z)(y+x)} + \dfrac{z}{(z+x)(z+y)}$ $= \dfrac{x}{(x+y)(x+z)} + \dfrac{y}{(y+z)(y+x)} + \dfrac{z}{(z+x)(z+y)}$

$= \dfrac{x(y+z) + y(x+z) + z(x+y)}{(x+y)(x+z)(y+z)}$ $= \dfrac{x(y+z) + y(x+z) + z(x+y)}{(x+y)(x+z)(y+z)}$

$= \dfrac{2xy+2yz + 2zx}{(x+y)(x+z)(y+z)}$ $= \dfrac{2xy+2yz + 2zx}{(x+y)(x+z)(y+z)}$

Ta cần chứng minh $\dfrac{2xy+2yz + 2zx}{(x+y)(x+z)(y+z)} \leq \dfrac{3}4$ $\dfrac{2xy+2yz + 2zx}{(x+y)(x+z)(y+z)} \leq \dfrac{3}4$

$\Leftrightarrow 8(xy+yz+zx) \leq 3(x+y)(y+z)(z+x)$ $\Leftrightarrow 8(xy+yz+zx) \leq 3(x+y)(y+z)(z+x)$

$\Leftrightarrow 8(xy+yz+zx)(x+y+z) \leq 9(x+y)(y+z)(z+x) (1)$ $\Leftrightarrow 8(xy+yz+zx)(x+y+z) \leq 9(x+y)(y+z)(z+x) (1)$

Thật vậy ta có

$(1)\ \Leftrightarrow 8(xy+yz+zx)(x+y+z) \leq 9(x+y)(yz+yx+z^2+xz)$ $(1)\ \Leftrightarrow 8(xy+yz+zx)(x+y+z) \leq 9(x+y)(yz+yx+z^2+xz)$

$\Leftrightarrow 8(xy+yz+zx)(x+y+z) \leq 9[(x+y)(yz+yx+xz)+z^2(x+y)]$ $\Leftrightarrow 8(xy+yz+zx)(x+y+z) \leq 9[(x+y)(yz+yx+xz)+z^2(x+y)]$

$\Leftrightarrow 8(xy+yz+zx)(x+y+z) \leq 9[(x+y+z)(yz+yx+xz)+z^2(x+y)-z(yz+yx+xz)]$ $\Leftrightarrow 8(xy+yz+zx)(x+y+z) \leq 9[(x+y+z)(yz+yx+xz)+z^2(x+y)-z(yz+yx+xz)]$

$\Leftrightarrow 8(xy+yz+zx)(x+y+z) \leq 9[(x+y+z)(yz+yx+xz)-xyz]$ $\Leftrightarrow 8(xy+yz+zx)(x+y+z) \leq 9[(x+y+z)(yz+yx+xz)-xyz]$

$\Leftrightarrow 9xyz \leq (x+y+z)(yz+yx+xz)$ $\Leftrightarrow 9xyz \leq (x+y+z)(yz+yx+xz)$

Áp dụng BĐT AM-GM ta có:

$x+y+z \geq \sqrt[3]{xyz}$ $x+y+z \geq \sqrt[3]{xyz}$

$xy+yz+zx \geq \sqrt[3]{(xyz)^2}$ $xy+yz+zx \geq \sqrt[3]{(xyz)^2}$

Nhân vế theo vế 2 BĐT trên ta có:

$(x+y+z)(yz+yx+xz) \geq 9xyz (đpcm)$ $(x+y+z)(yz+yx+xz) \geq 9xyz (đpcm)$

hay ta có (1) luôn đúng.

Tức là $P = \dfrac{x}{3x+yz} + \dfrac{y}{3y+zx} + \dfrac{z}{3z+xy} \leq \dfrac{3}4.$ $P = \dfrac{x}{3x+yz} + \dfrac{y}{3y+zx} + \dfrac{z}{3z+xy} \leq \dfrac{3}4.$

Vậy ${Max}_P = \dfrac{3}4 \Leftrightarrow x=y=z = 1.$ ${Max}_P = \dfrac{3}4 \Leftrightarrow x=y=z = 1.$

Câu III:

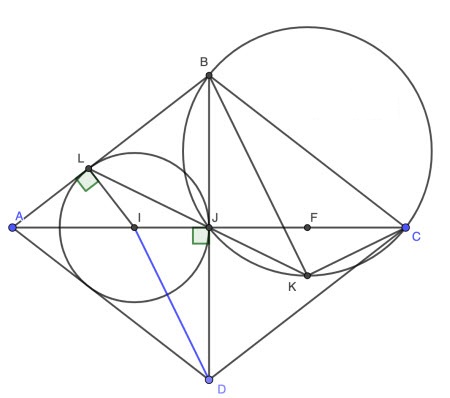
Đề thi thử vào lớp 10 môn Toán Chung Trường THPT Chuyên KHTN, Hà Nội năm 2020 (lần 2)

Vẽ đường tròn ngoại tiếp BJC.

Kẻ tia phân giác trong góc DBC cắt đường tròn ngoại tiếp BJC tại K'.

Dễ thấy $∠BK'C = ∠BJC = 90°$ (góc nội tiếp cùng chắn đường kính)

Vì BK là phân giác trong góc BDC nên

$∠JBK' = \dfrac{1}2∠JBC = \dfrac{1}2∠JDA = ∠JDI ⇒ BK' // DI.$

Vì tứ giác BJKC nội tiếp $⇒ ∠K'JC = ∠K'BC = \dfrac{1}2∠JBC$

Lại có $∠LJI = 90° - \dfrac{1}2∠LIJ = \dfrac{1}2(180° - ∠LIJ) = \dfrac{1}2∠JBA = \dfrac{1}2∠JBC = ∠K$ $∠LJI = 90° - \dfrac{1}2∠LIJ = \dfrac{1}2(180° - ∠LIJ) = \dfrac{1}2∠JBA = \dfrac{1}2∠JBC = ∠K'JC$

Suy ra L,J, K' thẳng hàng hay $K' ≡ K ⇒ ∠BKC = ∠BK'C = 90°$ hay KB ⊥ KC (đpcm)

Từ chứng minh phần 1), ta có:

$∠ILJ = ∠LJI = ∠KJC = ∠KBC = ∠KBJ = ∠KCJ$ hay ∠ILK = ∠KCI ⇒ Tứ giác LIKC nội tiếp (đpcm)

Lấy F là trung điểm JC.

Vì BK là tia phân giác trong của góc JBC ⇒ K là điểm chính giữa cung JC của đường tròn ngoại tiếp △JBC ⇒ KF ⊥ JC ⇒ KF // JB hay d(K;JB) = d(F;JB) = FJ

Ta có:

$S_{\triangle JBK} = \dfrac{1}2 JB.d_{(K;JB)} = \dfrac{1}2 JB.JF = \dfrac{1}2 JB.\dfrac{1}2 JC = \dfrac{1}2 S_{\triangle JBC}$ $S_{\triangle JBK} = \dfrac{1}2 JB.d_{(K;JB)} = \dfrac{1}2 JB.JF = \dfrac{1}2 JB.\dfrac{1}2 JC = \dfrac{1}2 S_{\triangle JBC}$

$\Leftrightarrow S_{\triangle JBK} =\dfrac{1}8 S_{ABCD} (đpcm)$ $\Leftrightarrow S_{\triangle JBK} =\dfrac{1}8 S_{ABCD} (đpcm)$

Câu IV:

Đặt $a = x^3; \space b = y^3; \space c = z^3$ $a = x^3; \space b = y^3; \space c = z^3$, ta có BĐT cần chứng minh tương đương với:

$\dfrac{x}{\sqrt[3]{y^3+z^3}} + \dfrac{y}{\sqrt[3]{z^3+x^3}} + \dfrac{z}{\sqrt[3]{x^3+y^3}} \geq 2$ $\dfrac{x}{\sqrt[3]{y^3+z^3}} + \dfrac{y}{\sqrt[3]{z^3+x^3}} + \dfrac{z}{\sqrt[3]{x^3+y^3}} \geq 2$

Ta đi chứng minh:

$\dfrac{x}{\sqrt[3]{y^3+z^3}} \geq \dfrac{x}{\sqrt{y^2+z^2}} (1)$ $\dfrac{x}{\sqrt[3]{y^3+z^3}} \geq \dfrac{x}{\sqrt{y^2+z^2}} (1)$

Thật vậy ta có:

$(1) \Leftrightarrow \left( \dfrac{x}{\sqrt[3]{y^3+z^3}} \right)^6 \geq \left( \dfrac{x}{\sqrt{y^2+z^2}} \right)^6$ $(1) \Leftrightarrow \left( \dfrac{x}{\sqrt[3]{y^3+z^3}} \right)^6 \geq \left( \dfrac{x}{\sqrt{y^2+z^2}} \right)^6$

$\Leftrightarrow (y^2+z^2)^3 \geq (y^3+z^3)^2$ $\Leftrightarrow (y^2+z^2)^3 \geq (y^3+z^3)^2$

$\Leftrightarrow 3y^2z^2(y^2+z^2) \geq 2y^3z^3$ $\Leftrightarrow 3y^2z^2(y^2+z^2) \geq 2y^3z^3$

$\Leftrightarrow y^2z^2(3y^2+3z^2 - 2yz) \geq 0$ $\Leftrightarrow y^2z^2(3y^2+3z^2 - 2yz) \geq 0$

$\Leftrightarrow y^2z^2[2y^2+2z^2 +(y-z)^2] \geq 0$ $\Leftrightarrow y^2z^2[2y^2+2z^2 +(y-z)^2] \geq 0$ (luôn đúng)

Hay ta có (1) luôn đúng (đpcm).

Áp dụng BĐT AM-GM ta có:

$x^2 + y^2 + z^2 \geq 2\sqrt{x^2(y^2+z^2)}$ $x^2 + y^2 + z^2 \geq 2\sqrt{x^2(y^2+z^2)}$

$\Leftrightarrow \dfrac{2x^2}{x^2 + y^2 + z^2} \leq \dfrac{x^2}{\sqrt{x^2(y^2+z^2)}} = \dfrac{x}{\sqrt{y^2+z^2}} \leq \dfrac{x}{\sqrt[3]{y^3+z^3}}$ $\Leftrightarrow \dfrac{2x^2}{x^2 + y^2 + z^2} \leq \dfrac{x^2}{\sqrt{x^2(y^2+z^2)}} = \dfrac{x}{\sqrt{y^2+z^2}} \leq \dfrac{x}{\sqrt[3]{y^3+z^3}}$

Chứng minh tương tự, ta có:

$\dfrac{2y^2}{x^2 + y^2 + z^2} \leq \dfrac{y}{\sqrt[3]{z^3+x^3}}$ $\dfrac{2y^2}{x^2 + y^2 + z^2} \leq \dfrac{y}{\sqrt[3]{z^3+x^3}}$

$\dfrac{2z^2}{x^2 + y^2 + z^2} \leq \dfrac{z}{\sqrt[3]{x^3+y^3}}$ $\dfrac{2z^2}{x^2 + y^2 + z^2} \leq \dfrac{z}{\sqrt[3]{x^3+y^3}}$

Cộng vế theo vế 3 BĐT trên ta có:

$\dfrac{x}{\sqrt[3]{y^3+z^3}} + \dfrac{y}{\sqrt[3]{z^3+x^3}} + \dfrac{z}{\sqrt[3]{x^3+y^3}} \geq \dfrac{2(x^2+y^2+z^2)}{x^2 + y^2 + z^2} = 2 (đpcm)$ $\dfrac{x}{\sqrt[3]{y^3+z^3}} + \dfrac{y}{\sqrt[3]{z^3+x^3}} + \dfrac{z}{\sqrt[3]{x^3+y^3}} \geq \dfrac{2(x^2+y^2+z^2)}{x^2 + y^2 + z^2} = 2 (đpcm)$

Hay ta có $\sqrt[3]{\dfrac{a}{b+c}} + \sqrt[3]{\dfrac{b}{c+a}} + \sqrt[3]{\dfrac{c}{a+b}} \geq 2.$ $\sqrt[3]{\dfrac{a}{b+c}} + \sqrt[3]{\dfrac{b}{c+a}} + \sqrt[3]{\dfrac{c}{a+b}} \geq 2.$

Dấu bằng xảy ra khi và chỉ khi a = 0, b = c và các hoán vị.

Đề thi thử vào lớp 10 môn Toán Chung Trường THPT Chuyên KHTN, Hà Nội năm 2020 (lần 2) được VnDoc chia sẻ trên đây với 4 câu hỏi tự luận với thời gian 120 phút, giúp các bạn học sinh có thêm tài liệu ôn tập chuẩn bị tốt cho kì thi sắp tới. Ngoài đề thi thử của Trường THPT Chuyên KHTN các bạn tham khảo các đề của các tỉnh khác nữa nhé

............................................

Ngoài Đề thi thử vào lớp 10 môn Toán Chung Trường THPT Chuyên KHTN, Hà Nội năm 2020 (lần 2). Mời các bạn học sinh còn có thể tham khảo các đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề Thi vào lớp 10 năm 2020 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt