Đáp án đề thi tuyển sinh lớp 10 môn Toán tỉnh Quảng Nam năm 2020

Đáp án đề thi môn Toán vào lớp 10 Quảng Nam

Đề thi tuyển sinh lớp 10 môn Toán Sở GD&ĐT Quảng Nam năm 2020

Đáp án đề thi tuyển sinh lớp 10 môn Toán tỉnh Quảng Nam năm 2020. Được VnDoc sưu tầm và đăng tải, kèm lời giải chi tiết cho các bạn đánh giá so sánh, hy vọng tài liệu này sẽ giúp ích cho các bạn học sinh ôn tập, chuẩn bị tốt cho kì thi vào lớp 10 THPT sắp tới. Mời các bạn cùng tham khảo

Lưu ý: Điểm chuẩn, điểm thi vào lớp 10 tỉnh Quảng Nam năm 2020

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 9, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 9 sau: Nhóm Tài liệu học tập lớp 9. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Đáp án đề thi tuyển sinh lớp 10 môn Toán tỉnh Quảng Nam năm 2020

Câu 1

a)

$A=2 \sqrt{27}-\sqrt{12}+\frac{3}{\sqrt{3}}$ $A=2 \sqrt{27}-\sqrt{12}+\frac{3}{\sqrt{3}}$

$=6 \sqrt{3}-2 \sqrt{3}+\sqrt{3}$ $=6 \sqrt{3}-2 \sqrt{3}+\sqrt{3}$

$=5\sqrt{3}$ $=5\sqrt{3}$

b)

$B=\frac{a-\sqrt{a}}{1-\sqrt{a}}+\frac{a-1}{\sqrt{a}+1}$ $B=\frac{a-\sqrt{a}}{1-\sqrt{a}}+\frac{a-1}{\sqrt{a}+1}$ với $a \geqslant 0 ; a \neq 1$ $a \geqslant 0 ; a \neq 1$

$=\frac{-\sqrt{a}(1-\sqrt{a})}{1-\sqrt{a}}+\frac{(\sqrt{a}-1)(\sqrt{a}+1)}{\sqrt{a}+1}$ $=\frac{-\sqrt{a}(1-\sqrt{a})}{1-\sqrt{a}}+\frac{(\sqrt{a}-1)(\sqrt{a}+1)}{\sqrt{a}+1}$

$=-\sqrt{a}+\sqrt{a}-1=-1$ $=-\sqrt{a}+\sqrt{a}-1=-1$

Câu 2

a) Cắt trục tung tại điểm có tung độ = 5 ⇒ B (0;5)

Theo bài ta có hệ PT $\left\{\begin{array}{l} 5=a \cdot 0+b \Leftrightarrow \\ 1=2 a+b \end{array}\right.\left\{\begin{matrix} b=5 \\ a=-2 \end{matrix}\right.$ $\left\{\begin{array}{l} 5=a \cdot 0+b \Leftrightarrow \\ 1=2 a+b \end{array}\right.\left\{\begin{matrix} b=5 \\ a=-2 \end{matrix}\right.$

KL

b) $(p): y=3 x^{2} ;(d): y=2 x+m$ $(p): y=3 x^{2} ;(d): y=2 x+m$

(P) ∩ (d) là nghiệm của PT

$3 x^{2}=2 x+m$ $3 x^{2}=2 x+m$

$\Leftrightarrow 3 x^{2}-2 x-m=0\ (*)$ $\Leftrightarrow 3 x^{2}-2 x-m=0\ (*)$

Để (P) ∩ (d) tại 1 điểm duy nhất ⇒ (*) có 1 nghiệm kép

$\Rightarrow \Delta^{\prime}-0 \Rightarrow \Delta^{\prime}=1^{2}-3 \cdot(-m)=0$ $\Rightarrow \Delta^{\prime}-0 \Rightarrow \Delta^{\prime}=1^{2}-3 \cdot(-m)=0$

$\Leftrightarrow \quad 3 m+1=0 \Leftrightarrow m=\frac{-1}{3}$ $\Leftrightarrow \quad 3 m+1=0 \Leftrightarrow m=\frac{-1}{3}$

Tọa độ giao điểm: $x_{1}=x_{1}=\frac{1}{3} \Rightarrow y=\frac{1}{3}$ $x_{1}=x_{1}=\frac{1}{3} \Rightarrow y=\frac{1}{3}$

KL. Vậy tọa độ điểm cần tìm $\left(\frac{1}{3};\frac{1}{3}\right)$ $\left(\frac{1}{3};\frac{1}{3}\right)$

Câu 3

$\text { a) } x^{4}+5 x^{2}-36=0$ $\text { a) } x^{4}+5 x^{2}-36=0$

$\Leftrightarrow x^{4}-4 x^{2}+9 x^{2}-36=0$ $\Leftrightarrow x^{4}-4 x^{2}+9 x^{2}-36=0$

$\Leftrightarrow x^{2}\left(x^{2}-4\right)+g\left(x^{2}-4\right)=0$ $\Leftrightarrow x^{2}\left(x^{2}-4\right)+g\left(x^{2}-4\right)=0$

$\Leftrightarrow\left(x^{2}+9\right)\left(x^{2}-4\right)=0$ $\Leftrightarrow\left(x^{2}+9\right)\left(x^{2}-4\right)=0$

$\Leftrightarrow \quad x^{2}-4=0$ $\Leftrightarrow \quad x^{2}-4=0$ (vì x² + 9 ≥ 9)

$(x-2)(x+2)=0$

$\Leftrightarrow\left[\begin{array}{l} x-2=0 \\ x+2=0 \end{array} \Leftrightarrow\left[\begin{array}{l} x=2 \\ x=-2 \end{array}\right.\right.$ $\Leftrightarrow\left[\begin{array}{l} x-2=0 \\ x+2=0 \end{array} \Leftrightarrow\left[\begin{array}{l} x=2 \\ x=-2 \end{array}\right.\right.$

KL

$b)\left\{ \begin{array}{l} x + 2y = 5\\ 2x - 3y = - 4 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} 2x + 4y = 10\\ 2x - 3y = - 4 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x = 1\\ y = 2 \end{array} \right.$ $b)\left\{ \begin{array}{l} x + 2y = 5\\ 2x - 3y = - 4 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} 2x + 4y = 10\\ 2x - 3y = - 4 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x = 1\\ y = 2 \end{array} \right.$

KL: (1;2)

$\text { c) } x^{2}-(2 m+1) x+4 m-3=0\ (1)$ $\text { c) } x^{2}-(2 m+1) x+4 m-3=0\ (1)$

Để (1) có 2 nghiệm x₁, x₂ phân biệt giả sử x₂ > 1; x₁<1 thì Δ

$\Delta=(2 m+1)^{2}-4 \cdot(4 m-3)$ $\Delta=(2 m+1)^{2}-4 \cdot(4 m-3)$

$=4 m^{2}-12 m+13$ $=4 m^{2}-12 m+13$

$=(2 m-3)^{2}+4>0\ \forall\ m$ $=(2 m-3)^{2}+4>0\ \forall\ m$

Vậy PT (1) luôn có 2 nghiệm x₁, x_{2 với ∀ m}

_{Để $x_2>1$ và $x_1<1$ thì $\left(x_{2}-1\right)\left(x_{1}-1\right)<0$}

$\Leftrightarrow x_{2} x_{1}-x_{1}-x_{2}+1<0$ $\Leftrightarrow x_{2} x_{1}-x_{1}-x_{2}+1<0$

$\Leftrightarrow x_{2} x_{1}-\left(x_{1}+x_{1}\right)+1<0\ (*)$ $\Leftrightarrow x_{2} x_{1}-\left(x_{1}+x_{1}\right)+1<0\ (*)$

Áp dụng Vi - ét ta có $\left\{\begin{array}{l} x_{1}+x_{2}=2 m+1 \\ x_{1} x_{2}=4 m-3 \end{array}\right. thế\ vào\ (*)$ $\left\{\begin{array}{l} x_{1}+x_{2}=2 m+1 \\ x_{1} x_{2}=4 m-3 \end{array}\right. thế\ vào\ (*)$

$(*) \Leftrightarrow \quad 4 m-3-(2 m+1)+1<0$ $(*) \Leftrightarrow \quad 4 m-3-(2 m+1)+1<0$

$\Leftrightarrow 2m-3<0 \Leftrightarrow m < \frac{3}{2}$ $\Leftrightarrow 2m-3<0 \Leftrightarrow m < \frac{3}{2}$

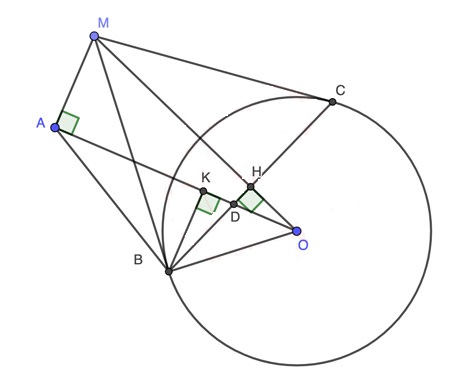
Đáp án đề thi tuyển sinh lớp 10 môn Toán tỉnh Quảng Nam năm 2020

Câu 4

a) vì MB; MC là tiếp tuyến tại B; C của $\Rightarrow \widehat{M B C}=\widehat{M C O}=90^{\circ}$ $\Rightarrow \widehat{M B C}=\widehat{M C O}=90^{\circ}$

⇒ Từ giác MBOC nội tiếp đường tròn đường kính MO (đpcm)

b)

Vì $\widehat{M A O}=\widehat{M B O}=\widehat{M C O}=90^{\circ}(\mathrm{g} t)$ $\widehat{M A O}=\widehat{M B O}=\widehat{M C O}=90^{\circ}(\mathrm{g} t)$⇒ 5 điểm A; M; C; O; B đồng viên

$\Rightarrow \widehat{B A O}=\widehat{B C O}$ $\Rightarrow \widehat{B A O}=\widehat{B C O}$ (góc nt cùng chắn cung BO)

Vì OM cắt BC tại H ⇒ $\widehat{B H O}=90^{\circ}$ $\widehat{B H O}=90^{\circ}$

Xét ΔAKB và ΔBHO có

$\left. \begin{array}{l} \widehat {AKB} = \widehat {BHO} = {90^0}\\ \widehat {BAK} = \widehat {BAO} = \widehat {BCO} = \widehat {CBO} = \widehat {OBH} \end{array} \right\} \Rightarrow \Delta AKB\sim\Delta BHO\ (g.g)$ $\left. \begin{array}{l} \widehat {AKB} = \widehat {BHO} = {90^0}\\ \widehat {BAK} = \widehat {BAO} = \widehat {BCO} = \widehat {CBO} = \widehat {OBH} \end{array} \right\} \Rightarrow \Delta AKB\sim\Delta BHO\ (g.g)$

$\Rightarrow \frac{K A}{K B}=\frac{H B}{H O} \Rightarrow K A \cdot H O=K B \cdot H B \quad\left(đpcm\right)$ $\Rightarrow \frac{K A}{K B}=\frac{H B}{H O} \Rightarrow K A \cdot H O=K B \cdot H B \quad\left(đpcm\right)$

c)

Xét ΔOBH và ΔOMB ta có:

$\left. \begin{array}{l} Góc\ \widehat {BOH}\ chung\\ \widehat {OHB} = \widehat {OBM}( = {90^0}) \end{array} \right\} \Rightarrow \Delta OBH\sim\Delta OMB(g.g)$ $\left. \begin{array}{l} Góc\ \widehat {BOH}\ chung\\ \widehat {OHB} = \widehat {OBM}( = {90^0}) \end{array} \right\} \Rightarrow \Delta OBH\sim\Delta OMB(g.g)$

$\Rightarrow \frac{O B}{O H}=\frac{O M}{O B} \Leftrightarrow O B^{2}=O M \cdot O H\ (1)$ $\Rightarrow \frac{O B}{O H}=\frac{O M}{O B} \Leftrightarrow O B^{2}=O M \cdot O H\ (1)$

Gọi $BC\cap AO=D$ $BC\cap AO=D$

Xét ΔODH và ΔOMA ta có:

$\left. \begin{array}{l}Góc\ \widehat {DOH}\ chung\\\widehat {OHD} = \widehat {OAM}( = {90^0})\end{array} \right\} \Rightarrow \Delta ODH\sim\Delta OMA(g.g)$ $\left. \begin{array}{l}Góc\ \widehat {DOH}\ chung\\\widehat {OHD} = \widehat {OAM}( = {90^0})\end{array} \right\} \Rightarrow \Delta ODH\sim\Delta OMA(g.g)$

$\Rightarrow \frac{O D}{O H}=\frac{OM}{O A} \Rightarrow O D \cdot OA=OM.OH\ (1)$ $\Rightarrow \frac{O D}{O H}=\frac{OM}{O A} \Rightarrow O D \cdot OA=OM.OH\ (1)$

Từ (1) và (2) ⇒OD . OA = OB²

$⇒\ OD=\frac{OB}{OA}$ $⇒\ OD=\frac{OB}{OA}$ không đổi

⇒ D cố định

⇒ BC luôn đi qua điểm D cố định, có $O D=\frac{O B^{2}}{O A}(\text { đpcm })$ $O D=\frac{O B^{2}}{O A}(\text { đpcm })$

Đề thi tuyển sinh lớp 10 môn Toán tỉnh Quảng Nam năm 2020

Đáp án đề thi tuyển sinh lớp 10 môn Toán tỉnh Quảng Nam năm 2020

Để chuẩn bị năm học mới vào lớp 10 các em tham gia vào nhóm Facebook do VnDoc chia sẻ, các em sẽ nhận trực tiếp các bài tập Toán, Văn, Tiếng Anh.. cùng các bài tập nâng cao cũng như các thông tin liên đến chương trình đào tạo lớp 10 khác hấp dẫn

Ngoài ra, VnDoc.com đã thành lập group chia sẻ tài liệu học tập THCS miễn phí trên Facebook: Tài liệu học tập lớp 10. Mời các bạn học sinh tham gia nhóm, để có thể nhận được những tài liệu mới nhất.

.............................................

Ngoài Đáp án đề thi tuyển sinh lớp 10 môn Toán tỉnh Quảng Nam năm 2020. Mời các bạn học sinh còn có thể tham khảo các đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề Thi vào lớp 10 năm 2024 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt

Chia sẻ, đánh giá bài viết

2

2.367

Bài trước

Bài sau