Đáp án đề thi tuyển sinh lớp 10 môn Toán Đà Nẵng năm 2021

Đề thi Toán vào lớp 10 Đà Nẵng 2021 - 2022 có đáp án

Đáp án đề thi tuyển sinh lớp 10 môn Toán Sở GD&ĐT Đà Nẵng năm 2021 - 2022 được VnDoc sưu tầm và đăng tải. Hy vọng đề thi này sẽ giúp ích cho các em học sinh có thêm tài liệu ôn tập chuẩn bị tốt cho kì thi vào lớp 10 sắp tới

Lưu ý: Tra cứu điểm thi tuyển sinh lớp 10 tỉnh Đà Nẵng năm 2021

Đáp án đề thi tuyển sinh lớp 10 môn Văn Đà Nẵng năm 2021

Đề thi vào lớp 10 môn Toán năm 2021 Đà Nẵng

1. Đáp án đề thi tuyển sinh lớp 10 môn Toán Đà Nẵng 2021
2. Đề thi tuyển sinh lớp 10 môn Toán Đà Nẵng 2021

1. Đáp án đề thi tuyển sinh lớp 10 môn Toán Đà Nẵng 2021

Hướng dẫn chi tiết đáp án

Câu 1

Câu 2

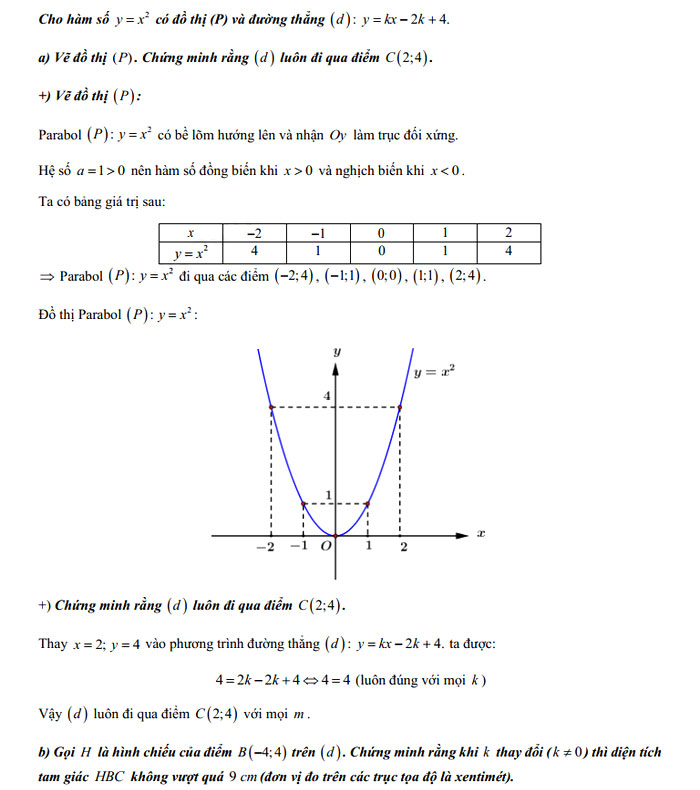
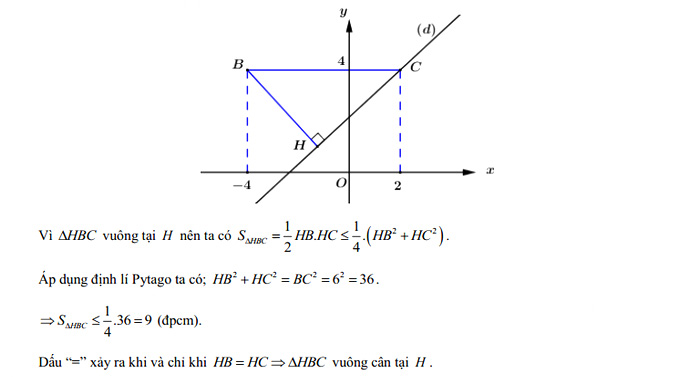
Câu 3

a) Với m = 2 thì phương trình trờ thành:

$x^{2}+4 x-12=0$ $x^{2}+4 x-12=0$

$\Leftrightarrow(x+6) \cdot(x-2)=0$ $\Leftrightarrow(x+6) \cdot(x-2)=0$

$\Leftrightarrow x=-6 \quad \vee \quad x=2$ $\Leftrightarrow x=-6 \quad \vee \quad x=2$

Vậy S={-6 ; 2}

b)

Phương trình có c.a = -12 <0 => pt có hai nghiệm trái dấu.

Theo định lí Viet ta có:

$\left\{\begin{array}{l} x_{1}+x_{2}=-4 m+4 \\ x_{1} \cdot x_{2}=-12 \end{array}\right.$ $\left\{\begin{array}{l} x_{1}+x_{2}=-4 m+4 \\ x_{1} \cdot x_{2}=-12 \end{array}\right.$

Xét yêu cầu bài toán.

$4 \cdot\left|x_{1}-2\right| \cdot \sqrt{4-m x_{2}}=\left(x_{1}+x_{2}-x_{1} x_{2}-8\right)^{2}$ $4 \cdot\left|x_{1}-2\right| \cdot \sqrt{4-m x_{2}}=\left(x_{1}+x_{2}-x_{1} x_{2}-8\right)^{2}$

Trong đó

$V P=(-4 m+4+12-8)^{2}=(-4 m+8)^{2}$ $V P=(-4 m+4+12-8)^{2}=(-4 m+8)^{2}$

Ngoài ra $x_2$ còn là nghiệm của phương trình nên:

$\begin{aligned} &x_{2}^{2}+4(m-1) \cdot x_{2}-12=0 \\ &\Leftrightarrow x_{2}^{2}-4 x_{2}+4=-4 m \cdot x_{2}+16 \\ &\Leftrightarrow\left(x_{2}-2\right)^{2}=4 \cdot\left(4-m x_{2}\right) \\ &\Leftrightarrow\left|x_{2}-2\right|=2 \cdot \sqrt{4-m x_{2}} \end{aligned}$ $\begin{aligned} &x_{2}^{2}+4(m-1) \cdot x_{2}-12=0 \\ &\Leftrightarrow x_{2}^{2}-4 x_{2}+4=-4 m \cdot x_{2}+16 \\ &\Leftrightarrow\left(x_{2}-2\right)^{2}=4 \cdot\left(4-m x_{2}\right) \\ &\Leftrightarrow\left|x_{2}-2\right|=2 \cdot \sqrt{4-m x_{2}} \end{aligned}$

Thay tất cả vào yêu cầu của bài toán ta được:

$\begin{aligned} &2 \cdot\left|x_{1}-2\right| \cdot\left|x_{2}-2\right|=(-4 m+8)^{2} \\ &\Leftrightarrow 2 \cdot\left|x_{1} x_{2}-2\left(x_{1}+x_{2}\right)+4\right|=(-4 m+8)^{2} \\ &\Leftrightarrow 2 \cdot|-12+8 m-8+4|=(-4 m+8)^{2} \\ &\Leftrightarrow 16 \cdot|m-2|=16 \cdot(m-2)^{2} \\ &\Leftrightarrow|m-2|=|m-2|^{2} \\ &\Leftrightarrow|m-2|=0 \quad \vee \quad|m-2|=1 \\ &\Leftrightarrow m=2 \vee m=3 \quad \vee \quad m=1 \end{aligned}$ $\begin{aligned} &2 \cdot\left|x_{1}-2\right| \cdot\left|x_{2}-2\right|=(-4 m+8)^{2} \\ &\Leftrightarrow 2 \cdot\left|x_{1} x_{2}-2\left(x_{1}+x_{2}\right)+4\right|=(-4 m+8)^{2} \\ &\Leftrightarrow 2 \cdot|-12+8 m-8+4|=(-4 m+8)^{2} \\ &\Leftrightarrow 16 \cdot|m-2|=16 \cdot(m-2)^{2} \\ &\Leftrightarrow|m-2|=|m-2|^{2} \\ &\Leftrightarrow|m-2|=0 \quad \vee \quad|m-2|=1 \\ &\Leftrightarrow m=2 \vee m=3 \quad \vee \quad m=1 \end{aligned}$

Vậy $m \in\{1 ; 2 ; 3\}$ $m \in\{1 ; 2 ; 3\}$

Câu 4

Bài 5.

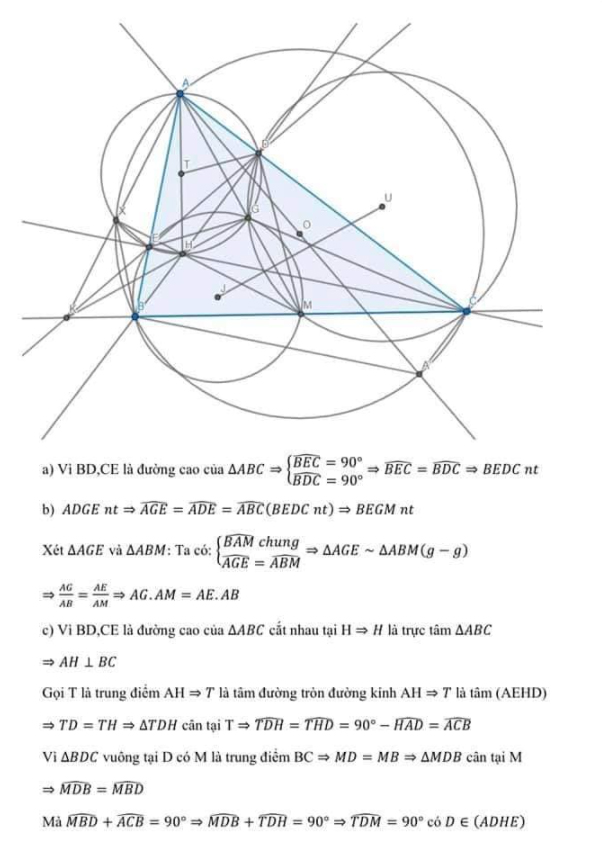
Đáp án đề thi tuyển sinh lớp 10 môn Toán Đà Nẵng 2021

Ngắn gọn hơn:

$a) \widehat{B D C}=\widehat{B E C}=90^{\circ}$ $a) \widehat{B D C}=\widehat{B E C}=90^{\circ}$

=> BEDC nội tiếp (tứ giác có hai đỉnh liền kề cùng nhìn cạnh đối diện dưới góc bằng nhau.)

$b) \widehat{A E H}=\overline{A D H}=90^{\circ}(\mathrm{gt})$ $b) \widehat{A E H}=\overline{A D H}=90^{\circ}(\mathrm{gt})$

=> AEHD nội tiếp trong đường tròn đương kinh A H.

Xét đường tròn này thì $\widehat{G}=\widehat{D}$ $\widehat{G}=\widehat{D}$ (củng chắn cung AE )

lại có $\widehat{D}=\widehat{B}$ $\widehat{D}=\widehat{B}$ (BEDC nội tiếp $\Rightarrow \widehat{G}=\widehat{B}$ $\Rightarrow \widehat{G}=\widehat{B}$

từ đây ta chứng minh được $\triangle A G E∽ \triangle A B M(g-g)$ $\triangle A G E∽ \triangle A B M(g-g)$

$\Rightarrow \dfrac{A G}{A E}=\frac{A B}{A M} \Rightarrow A G \cdot A M=A E \cdot A B$ $\Rightarrow \dfrac{A G}{A E}=\frac{A B}{A M} \Rightarrow A G \cdot A M=A E \cdot A B$

c)

Cách 1: Gọi N là tâm đường tròn đường kính AH.

Ta chứng minh được MD là tiếp tuyến của đường tròn đường kính AH,

$PT -2: MD² = MG. MA mà MD = MC$ (định lí đường trung tuyến ứng với cạnh huyền áp dụng cho ABDC)

→ MC² = MG. MA → △MGC ∽ △MCA (c-g-c)

+ ∠C = ∠A

Cách 2: đã có AE.AB = AG.AM

ta lại chứng minh được AE • AB = AD. AC (vì △ADE ∽△AABC (g-g).

→ AG. AM = ADAC

=>DGMC nội tiếp.

=> ∠D = ∠C mà ∠D = ∠A (cũng chắn cung DG của đường tròn đường kính AH) nên ∠C = ∠A

2. Đề thi tuyển sinh lớp 10 môn Toán Đà Nẵng 2021

Đề thi tuyển sinh lớp 10 môn Toán Đà Nẵng 2021

Ngoài ra, VnDoc.com đã thành lập group chia sẻ tài liệu học tập THPT miễn phí trên Facebook: Tài liệu học tập lớp 10. Mời các bạn học sinh tham gia nhóm, để có thể nhận được những tài liệu mới nhất.

Để ôn tập và chuẩn bị tốt hơn cho kì thi vào lớp 10 các bạn tham khảo đề thi vào lớp 10 của các tỉnh khác nhé

.............................................

Ngoài Đáp án đề thi tuyển sinh lớp 10 môn Toán Đà Nẵng năm 2021. Mời các bạn học sinh còn có thể tham khảo các đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề Thi vào lớp 10 năm 2024 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt

Chia sẻ, đánh giá bài viết

4

4.045

Bài trước

Bài sau