Đáp án đề thi tuyển sinh lớp 10 môn Toán chuyên năm 2020 Trung học Thực hành TPHCM

Đề thi tuyển sinh vào lớp 10 môn Toán năm 2020 có đáp án

Đề thi tuyển sinh lớp 10 môn Toán chuyênTrung học Thực hành TPHCM năm 2020

Đáp án đề thi tuyển sinh lớp 10 môn Toán chuyên năm 2020 Trung học Thực hành TPHCM do thư viện đề thi VnDoc.com sưu tầm. Đây là đề thi vào lớp 10 dành cho các bạn học sinh ôn tập, củng cố kiến thức, rèn luyện kĩ năng làm bài Toán. Mời các bạn cùng tham khảo

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 9, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 9 sau: Nhóm Tài liệu học tập lớp 9. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Đáp án đề thi tuyển sinh lớp 10 môn Toán chuyên năm 2020 Trung học Thực hành TPHCM

Câu 1:

a) Xem hình

b)

Xét phương trình hoành độ giao điểm của (P) và (d') ta có:

$-x^2 = -mx - 4$

$\Leftrightarrow x^{2} -mx-4=0 (*)$ $\Leftrightarrow x^{2} -mx-4=0 (*)$

Để (P) cắt (d') tại hai điểm phân biệt khi và chỉ khi (*) có hai nghiệm phân biệt, hay:

$\Delta = m^2 + 16 >0$ $\Delta = m^2 + 16 >0$ với mọi m.

Áp dụng hệ thức Vi-ét, ta có:

$\left\{ \matrix{ x_1+x_2 = m \hfill \cr x_1x_2 = -4 \hfill \cr} \right.$ $\left\{ \matrix{ x_1+x_2 = m \hfill \cr x_1x_2 = -4 \hfill \cr} \right.$

Ta có:

$y_1^2 + y_2^2 = 49$

$\Leftrightarrow x_1^4 + x_2^4 = 49$ $\Leftrightarrow x_1^4 + x_2^4 = 49$

$\Leftrightarrow (x_1^2 + x_2^2)^2 - 2x_1^2x_2^2 = 49$ $\Leftrightarrow (x_1^2 + x_2^2)^2 - 2x_1^2x_2^2 = 49$

$\Leftrightarrow [(x_1 + x_2)^2-2x_1x_2]^2 - 2x_1^2x_2^2 = 49$ $\Leftrightarrow [(x_1 + x_2)^2-2x_1x_2]^2 - 2x_1^2x_2^2 = 49$

$\Leftrightarrow (m^2+8)^2 - 2.(-4)^2= 49$ $\Leftrightarrow (m^2+8)^2 - 2.(-4)^2= 49$

$\Leftrightarrow m^4 + 16m^2 -17 = 0$ $\Leftrightarrow m^4 + 16m^2 -17 = 0$

$\Leftrightarrow \left[ \matrix{ m^2 = 1 \Rightarrow m = ±1 & (tm) \hfill \cr m^2 = -17 & (loại) \hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ m^2 = 1 \Rightarrow m = ±1 & (tm) \hfill \cr m^2 = -17 & (loại) \hfill \cr} \right.$

KL...

Câu 2:

Để phương trình có 2 nghiệm phân biệt

$⇔\Delta = 1^2 - 4 + 4m = 4m -3 >0 ⇔ m > \dfrac{3}4$ $⇔\Delta = 1^2 - 4 + 4m = 4m -3 >0 ⇔ m > \dfrac{3}4$

Áp dụng hệ thức Vi-ét, ta có:

$\left\{ \matrix{ x_1+x_2 = -1 \hfill \cr x_1x_2 = 1-m \hfill \cr} \right.$ $\left\{ \matrix{ x_1+x_2 = -1 \hfill \cr x_1x_2 = 1-m \hfill \cr} \right.$

Ta có:

$\dfrac{1}{x_1^2} + \dfrac{1}{x_2^2} \leq \dfrac{5}{(x_1x_2)^2}$ $\dfrac{1}{x_1^2} + \dfrac{1}{x_2^2} \leq \dfrac{5}{(x_1x_2)^2}$ (đkxđ: $x_1x_2 ≠ 0 ⇔ m ≠1$)

$⇔ \dfrac{x_1^2 + x_2^2}{(x_1x_2)^2} \leq \dfrac{5}{(x_1x_2)^2}$ $⇔ \dfrac{x_1^2 + x_2^2}{(x_1x_2)^2} \leq \dfrac{5}{(x_1x_2)^2}$

$⇔ x_1^2 + x_2^2 \leq 5$ $⇔ x_1^2 + x_2^2 \leq 5$

$⇔ (x_1+ x_2)^2 - 2x_1x_2 \leq 5$ $⇔ (x_1+ x_2)^2 - 2x_1x_2 \leq 5$

$⇔ 1 - 2(1-m) \leq 5$ $⇔ 1 - 2(1-m) \leq 5$

$⇔ m \leq 3$ $⇔ m \leq 3$

Vậy $\dfrac{3}4 < m \leq 3; m ≠ 1$ $\dfrac{3}4 < m \leq 3; m ≠ 1$

Câu 3:

Ta có:

$VT = \left( \sqrt a - \sqrt b \right) \left( \dfrac{a\sqrt a - b\sqrt b}{a-b} + \dfrac{1}{\dfrac{1}{\sqrt a}+\dfrac{1}{\sqrt b}} \right)$ $VT = \left( \sqrt a - \sqrt b \right) \left( \dfrac{a\sqrt a - b\sqrt b}{a-b} + \dfrac{1}{\dfrac{1}{\sqrt a}+\dfrac{1}{\sqrt b}} \right)$

$=\left( \sqrt a - \sqrt b \right) \left( \dfrac{(\sqrt a - \sqrt b)(a+ \sqrt {ab} + b)}{(\sqrt a - \sqrt b)(\sqrt a + \sqrt b)} + \dfrac{ \sqrt {ab} }{\sqrt a + \sqrt b} \right)$ $=\left( \sqrt a - \sqrt b \right) \left( \dfrac{(\sqrt a - \sqrt b)(a+ \sqrt {ab} + b)}{(\sqrt a - \sqrt b)(\sqrt a + \sqrt b)} + \dfrac{ \sqrt {ab} }{\sqrt a + \sqrt b} \right)$

$= \left( \sqrt a - \sqrt b \right) \left( \dfrac{a+ \sqrt {ab} + b}{\sqrt a + \sqrt b} + \dfrac{ \sqrt {ab} }{\sqrt a + \sqrt b} \right)$ $= \left( \sqrt a - \sqrt b \right) \left( \dfrac{a+ \sqrt {ab} + b}{\sqrt a + \sqrt b} + \dfrac{ \sqrt {ab} }{\sqrt a + \sqrt b} \right)$

$= \left( \sqrt a - \sqrt b \right) \left( \dfrac{a+ 2\sqrt {ab} + b}{\sqrt a + \sqrt b}\right)$ $= \left( \sqrt a - \sqrt b \right) \left( \dfrac{a+ 2\sqrt {ab} + b}{\sqrt a + \sqrt b}\right)$

$= \left( \sqrt a - \sqrt b \right) \left( \dfrac{(\sqrt a + \sqrt b)^2}{\sqrt a + \sqrt b}\right)$ $= \left( \sqrt a - \sqrt b \right) \left( \dfrac{(\sqrt a + \sqrt b)^2}{\sqrt a + \sqrt b}\right)$

$= \left( \sqrt a - \sqrt b \right) \left( \sqrt a + \sqrt b\right)$ $= \left( \sqrt a - \sqrt b \right) \left( \sqrt a + \sqrt b\right)$

$= a-b$

Hay $\left( \sqrt a - \sqrt b \right) \left( \dfrac{a\sqrt a - b\sqrt b}{a-b} + \dfrac{1}{\dfrac{1}{\sqrt a}+\dfrac{1}{\sqrt b}} \right) = a-b$ $\left( \sqrt a - \sqrt b \right) \left( \dfrac{a\sqrt a - b\sqrt b}{a-b} + \dfrac{1}{\dfrac{1}{\sqrt a}+\dfrac{1}{\sqrt b}} \right) = a-b$

(đpcm)

KL....

Câu 4:

$\dfrac{x^4}{1+x^2 - 2x} + \dfrac{1}{1-x} = 3+ x$ $\dfrac{x^4}{1+x^2 - 2x} + \dfrac{1}{1-x} = 3+ x$

ĐKXĐ: x ≠ 1.

$⇔ \dfrac{x^4+1-x}{(x-1)^2} = 3+ x$ $⇔ \dfrac{x^4+1-x}{(x-1)^2} = 3+ x$

$⇔ x^4 - x + 1 = (3+ x)(x-1)^2$

$⇔ x^4 - x + 1 = (x + 3)(x^2 - 2x + 1)$

$⇔ x^4 - x + 1 = x^3 + x^2 - 5x + 3$

$⇔ x^4 -x^3 - x^2 + 4x - 2 = 0$

$⇔ (x^2 + x -1) (x^2 -2x + 2) = 0$

Vì $⇔x^2 -2x + 2 = (x-1)^2 + 1 > 0$ nên:

$x^2 + x -1 = 0$

$⇔ \left[ \matrix{ {x} = \dfrac{-1+\sqrt 5}2 \hfill \cr {x} = \dfrac{-1-\sqrt 5}2 \hfill \cr} \right.$ $⇔ \left[ \matrix{ {x} = \dfrac{-1+\sqrt 5}2 \hfill \cr {x} = \dfrac{-1-\sqrt 5}2 \hfill \cr} \right.$ (tm đkxđ)

KL....

Câu 5:

Gọi số bạn được 9 điểm là A (học sinh, A ∈ ℕ*)

Gọi số học sinh trong 1 tổ là X (học sinh, X ∈ ℕ*)

Vì lớp có 4 tổ, mỗi tổ có số học sinh bằng nhau ⇒ Tổng số học sinh của lớp là:$4X (4X > A)$

Theo bài ra ta có:

$9A + 8(4X - A) = 336$

$⇔A+32X=336>32X⇒X<10,5$

Lại có $4X>A⇒336=A+32X<4X+32X=36X⇒9,3<X$

Mà X ∈ ℕ^*, 9,3 < X < 10,5 ⇒ X = 10 (học sinh)

⇒ A = 336 - 32 x 10 = 16 (học sinh) (tm đk)

KL...

Câu 6:

Gọi cạnh tấm tôn ban đầu là a (cm; a > 4)

Ta có:

$V_{hộp} = h.(a-4)^2 = 128 ⇔ (a-4)^2 = \dfrac{128}h = \dfrac{128}2 = 64$ $V_{hộp} = h.(a-4)^2 = 128 ⇔ (a-4)^2 = \dfrac{128}h = \dfrac{128}2 = 64$

$⇔a-4=8⇔a=12(cm)$

Diện tích tấm tôn ban đầu là:

$S = a^2 = 144 \space ({cm}^2)$ $S = a^2 = 144 \space ({cm}^2)$

KL....

Câu 7:

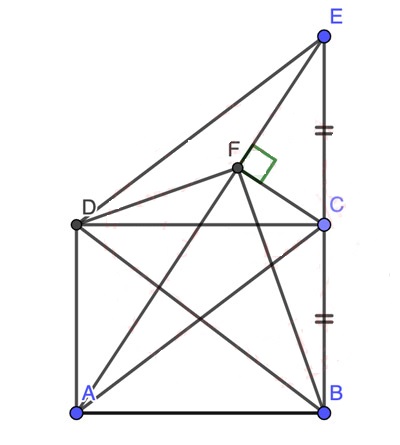
Đáp án đề thi tuyển sinh lớp 10 môn Toán chuyên năm 2020 Trung học Thực hành TPHCM

a)

Theo giả thiết, ta có: ∠ADC = ∠AFC = 90° ⇒ Tứ giác CADF nội tiếp đường tròn đường kính CA (đpcm)

⇒ ∠DFA = ∠DCA = ∠DBA

⇒ Tứ giác DFBA nội tiếp ⇒ ∠BFD + ∠BAD = 180° ⇒ ∠BFD = 180° - ∠BAD = 90° (đpcm)

b)

Xét △EFC và △EBA có:

Góc ∠FEC chung

∠EFC = ∠EBA = 90°

Suy ra $\triangle E F C \sim \Delta E B A \Rightarrow \frac{C F}{A B}=\frac{E C}{E A}$ $\triangle E F C \sim \Delta E B A \Rightarrow \frac{C F}{A B}=\frac{E C}{E A}$

$\Rightarrow C F=\frac{E C \cdot A B}{E A}=\frac{C B \cdot A B}{\sqrt{E B^{2}+B A^{2}}}=\frac{C B \cdot A B}{\sqrt{4 C B^{2}+B A^{2}}}=\frac{3.4}{\sqrt{4.9+16}}=\frac{6}{\sqrt{13}}(\mathrm{cm})$ $\Rightarrow C F=\frac{E C \cdot A B}{E A}=\frac{C B \cdot A B}{\sqrt{E B^{2}+B A^{2}}}=\frac{C B \cdot A B}{\sqrt{4 C B^{2}+B A^{2}}}=\frac{3.4}{\sqrt{4.9+16}}=\frac{6}{\sqrt{13}}(\mathrm{cm})$

Ta có:

$\dfrac{S_{\triangle DEF}}{S_{\triangle DAE}} = \dfrac{EF}{AE}$ $\dfrac{S_{\triangle DEF}}{S_{\triangle DAE}} = \dfrac{EF}{AE}$

$⇒ S_{\triangle DEF}= \dfrac{EF}{AE}.S_{\triangle DAE} = \dfrac{EF}{AE}(S_{ABED} - S_{\triangle EAB}) = \dfrac{EF}{AE}[\dfrac{1}2.(AD+BE).AB - \dfrac{1}2.BE.AB]$ $⇒ S_{\triangle DEF}= \dfrac{EF}{AE}.S_{\triangle DAE} = \dfrac{EF}{AE}(S_{ABED} - S_{\triangle EAB}) = \dfrac{EF}{AE}[\dfrac{1}2.(AD+BE).AB - \dfrac{1}2.BE.AB]$

$= \dfrac{\sqrt{{EC}^2-{FC}^2}}{\sqrt{{EB}^2+{BA}^2}}(\dfrac{1}2.3.AD.AB - \dfrac{1}2.2.AD.AB)$ $= \dfrac{\sqrt{{EC}^2-{FC}^2}}{\sqrt{{EB}^2+{BA}^2}}(\dfrac{1}2.3.AD.AB - \dfrac{1}2.2.AD.AB)$

$= \dfrac{\sqrt{{3}^2-{\dfrac{36}{13}}}}{\sqrt{4.3^2+4^2}}(\dfrac{1}2.3.3.4 - \dfrac{1}2.2.3.4)$ $= \dfrac{\sqrt{{3}^2-{\dfrac{36}{13}}}}{\sqrt{4.3^2+4^2}}(\dfrac{1}2.3.3.4 - \dfrac{1}2.2.3.4)$

$= \dfrac{\dfrac{9}{\sqrt{13}}}{2\sqrt{13}}.6$ $= \dfrac{\dfrac{9}{\sqrt{13}}}{2\sqrt{13}}.6$

$= \dfrac{27}{13} \space ({cm}^2)$ $= \dfrac{27}{13} \space ({cm}^2)$

KL...

Câu 8:

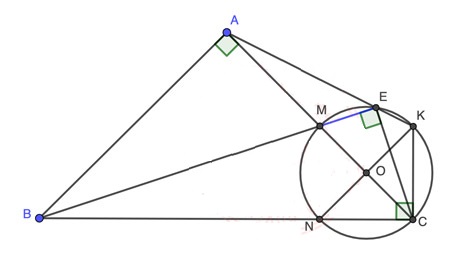
Đáp án đề thi tuyển sinh lớp 10 môn Toán chuyên năm 2020 Trung học Thực hành TPHCM

Vì △ABC vuông cân tại A ⇒ ∠ABC = ∠ACB = 45°.

△ONC cân tại O (do ON = OC) ⇒ ∠ONC = ∠OCN = 45° ⇒ ∠NOC = 90°.

Tương tự, ta có MNCK là hình vuông (do 2 đường chéo MC ⊥ NK và cắt nhau tại trung điểm mỗi đường)

Suy ra △ABC ∽ △KCM (hai △ cùng vuông cân) $\Rightarrow \frac{A C}{B C}=\frac{K C}{M C} \Rightarrow \frac{A C}{K C}=\frac{B C}{M C}$ $\Rightarrow \frac{A C}{B C}=\frac{K C}{M C} \Rightarrow \frac{A C}{K C}=\frac{B C}{M C}$

Xét △CMB và △CKA, ta có:

$\frac{A C}{K C}=\frac{B C}{M C}(\mathrm{cmt})$ $\frac{A C}{K C}=\frac{B C}{M C}(\mathrm{cmt})$

∠BCM = ∠ACK = 45°

Suy ra △CMB ∽ △CKA ⇒ ∠BMC = ∠AKC

Lại có tứ giác MEKC nội tiếp ⇒ ∠EKC + ∠EMC = 180° ⇒ ∠AKC = ∠EKC = 180° - ∠EMC

Suy ra ∠BMC = 180° - ∠EMC ⇒ ∠BMC + ∠EMC = 180° hay ∠BME = 180°

hay B,M,E thẳng hàng (đpcm).

Đề thi tuyển sinh lớp 10 môn Toán chuyên năm 2020 Trung học Thực hành TPHCM

Đáp án đề thi tuyển sinh lớp 10 môn Toán chuyên năm 2020 Trung học Thực hành TPHCM

Để chuẩn bị năm học mới vào lớp 10 các em tham gia vào nhóm Facebook do VnDoc chia sẻ, các em sẽ nhận trực tiếp các bài tập Toán, Văn, Tiếng Anh.. cùng các bài tập nâng cao cũng như các thông tin liên đến chương trình đào tạo lớp 10 khác hấp dẫn

Ngoài ra, VnDoc.com đã thành lập group chia sẻ tài liệu học tập THCS miễn phí trên Facebook: Tài liệu học tập lớp 10. Mời các bạn học sinh tham gia nhóm, để có thể nhận được những tài liệu mới nhất.

.............................................

Ngoài Đáp án đề thi tuyển sinh lớp 10 môn Toán chuyên năm 2020 tỉnh Thái Bình. Mời các bạn học sinh còn có thể tham khảo các đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề Thi vào lớp 10 năm 2024 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt

Chia sẻ, đánh giá bài viết

1

224

Bài trước

Bài sau