Đề thi thử vào lớp 10 môn Toán Trường THCS Bình Dương, Quảng Ninh năm 2020 (Mã 2)

Đề tuyển sinh vào 10 môn Toán năm 2020 có đáp án

Đề thi thử vào lớp 10 môn Toán Trường THCS Bình Dương năm 2020

VnDoc xin giới thiệu Đề thi thử vào lớp 10 môn Toán Trường THCS Bình Dương, Quảng Ninh năm 2020 (Mã 2). Đề thi vào lớp 10 môn Toán này sẽ giúp các bạn học sinh tự ôn luyện và hệ thống lại kiến thức, chuẩn bị tốt cho ôn thi vào lớp 10 các trường THPT sắp tới. Mời các bạn tham khảo.

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 9, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 9 sau: Nhóm Tài liệu học tập lớp 9. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Bài 1: (1,5 điểm)

a) Tính: $2\sqrt{25} + 3\sqrt{4}$ $2\sqrt{25} + 3\sqrt{4}$

b) Rút gọn biểu thức

$A = \left( \dfrac{\sqrt x}{\sqrt x + 2} + \dfrac{2}{\sqrt x - 2} \right): \dfrac{x+4}{\sqrt x + 2}$ $A = \left( \dfrac{\sqrt x}{\sqrt x + 2} + \dfrac{2}{\sqrt x - 2} \right): \dfrac{x+4}{\sqrt x + 2}$

với $x \geq 0; x ≠4$ $x \geq 0; x ≠4$

c) Giải phương trình bậc hai:

$x^2 - 2x - 2 =0$

Bài 2: (1,5 điểm)

Cho parabol $(P): y = x^2$ và đường thẳng (d): $y = (m-1)x + m + 4$ (tham số m)

a) Tìm m để (d) đi qua điểm A(2;5).

b) Với m = 2, tìm toạ độ giao điểm của (P) và (d).

c) Tìm m để (d) cắt (P) tại hai điểm nằm về hai phía của trục tung.

Bài 3: (2,0 điểm)

Cho hệ phương trình (tham số m):

$\left\{ \matrix{ x+ y = 3m + 2 \hfill \cr 3x - 2y = 11 - m \hfill \cr} \right.$ $\left\{ \matrix{ x+ y = 3m + 2 \hfill \cr 3x - 2y = 11 - m \hfill \cr} \right.$

a) Giải hệ phương trình với m = 2.

b) Tìm m để hệ đã cho có nghiệm (x;y) thoả mãn $y^2 - 8x^2$ đạt giá trị lớn nhất.

Bài 4: (2,0 điểm)

Lớp 9A dự định trồng 420 cây xanh. Đến ngày thực hiện có 7 bạn không tham gia do được triệu tập học bồi dưỡng đội tuyển học sinh giỏi của nhà trường nên mỗi bạn còn lại phải trồng thêm 3 cây mới đảm bảo kế hoạch đặt ra. Hỏi lớp 9A có bao nhiêu học sinh.

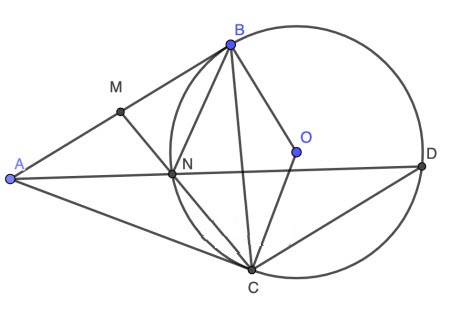
Bài 5: (3,0 điểm) Cho điểm A nằm bên ngoài đường tròn (O). Từ A kẻ hai tiếp tuyến AB, AC với đường tròn đó (B,C là các tiếp điểm). Gọi M là trung điểm của AB. Đường thẳng MC cắt đường tròn (O) tại N (N khác C).

a) Chứng minh ABOC là tứ giác nội tiếp.

b) Chứng minh $MB² = MN.MC.$

c) Tia AN cắt đường tròn (O) tại D (D khác N). Chứng minh: ∠MAN = ∠ADC.

Hết

Đáp án đề thi thử vào lớp 10 môn Toán Trường THCS Bình Dương năm 2020

Bài 1:

$a)\ 2\sqrt{25} + 3\sqrt{4} = 2.5 + 3.2 = 16$ $a)\ 2\sqrt{25} + 3\sqrt{4} = 2.5 + 3.2 = 16$

b)

Với $x \geq 0; x ≠4$ $x \geq 0; x ≠4$, ta có:

$A = \left( \dfrac{\sqrt x}{\sqrt x + 2} + \dfrac{2}{\sqrt x - 2} \right): \dfrac{x+4}{\sqrt x + 2}$ $A = \left( \dfrac{\sqrt x}{\sqrt x + 2} + \dfrac{2}{\sqrt x - 2} \right): \dfrac{x+4}{\sqrt x + 2}$

$= \dfrac{\sqrt x(\sqrt x - 2) + 2(\sqrt x + 2)}{(\sqrt x + 2)(\sqrt x - 2)}. \dfrac{\sqrt x + 2}{x+4}$ $= \dfrac{\sqrt x(\sqrt x - 2) + 2(\sqrt x + 2)}{(\sqrt x + 2)(\sqrt x - 2)}. \dfrac{\sqrt x + 2}{x+4}$

$= \dfrac{x + 4}{(\sqrt x + 2)(\sqrt x - 2)}. \dfrac{\sqrt x + 2}{x+4} = \dfrac{1}{\sqrt x - 2}$ $= \dfrac{x + 4}{(\sqrt x + 2)(\sqrt x - 2)}. \dfrac{\sqrt x + 2}{x+4} = \dfrac{1}{\sqrt x - 2}$

c)

$x^2 - 2x - 2 =0$

$\Leftrightarrow \left[ \matrix{ {x} = 1+\sqrt 3 \hfill \cr {x} = 1-\sqrt 3 \hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ {x} = 1+\sqrt 3 \hfill \cr {x} = 1-\sqrt 3 \hfill \cr} \right.$

Bài 2:

a)

Để (d) đi quả A(2;5) thì toạ độ điểm A phải thoả mãn phương trình đường thẳng (d), tức là:

$5 = (m-1).2 + m + 4$

$\Leftrightarrow m =1$ $\Leftrightarrow m =1$

b)

Với m = 2 ta có:

(d): y = x + 6

Phương trình hoành độ giao điểm của (P) và (d) là:

$x^2 = x+ 6$

$\Leftrightarrow x^2 - x - 6 = 0$ $\Leftrightarrow x^2 - x - 6 = 0$

$\Leftrightarrow \left[ \matrix{ {x} = 3 \Rightarrow y = 9 \hfill \cr {x} = -2 \Rightarrow y = 4 \hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ {x} = 3 \Rightarrow y = 9 \hfill \cr {x} = -2 \Rightarrow y = 4 \hfill \cr} \right.$

c)

Để (d) cắt (P) tại hai điểm phân biệt ⇔

$x^2 = (m-1)x + m + 4 \Leftrightarrow x^2 - (m-1) x - m - 4 = 0(*)$ $x^2 = (m-1)x + m + 4 \Leftrightarrow x^2 - (m-1) x - m - 4 = 0(*)$

có hai nghiệm phân biệt ⇔

$\Delta = (m-1)^2 + 4m + 16 = m^2 + 2m + 17 > 0$ $\Delta = (m-1)^2 + 4m + 16 = m^2 + 2m + 17 > 0$ với mọi m.

Gọi $A(x_a;y_a)$ và $B(x_b;y_b)$ là giao điểm của (d) và (P).

Áp dụng hệ thức Vi-ét cho (*) ta có:

$\left\{ \matrix{ x_a+x_b = m-1 \hfill \cr x_ax_b = -m-4 \hfill \cr} \right.$ $\left\{ \matrix{ x_a+x_b = m-1 \hfill \cr x_ax_b = -m-4 \hfill \cr} \right.$

Để hai điểm nằm về hai phía của trục tung thì $x_a.x_b < 0$

$\Leftrightarrow -m-4 < 0 \Leftrightarrow m > -4.$ $\Leftrightarrow -m-4 < 0 \Leftrightarrow m > -4.$

Bài 3:

Cho hệ phương trình (tham số m):

$\left\{ \matrix{ x+ y = 3m + 2 \hfill \cr 3x - 2y = 11 - m \hfill \cr} \right.$ $\left\{ \matrix{ x+ y = 3m + 2 \hfill \cr 3x - 2y = 11 - m \hfill \cr} \right.$

a)

Với m = 2 ta có:

$\left\{ \matrix{ x+ y = 3.2 + 2 = 8 \hfill \cr 3x - 2y = 11 - 2 = 9 \hfill \cr} \right.$ $\left\{ \matrix{ x+ y = 3.2 + 2 = 8 \hfill \cr 3x - 2y = 11 - 2 = 9 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x=5 \hfill \cr y =3 \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ x=5 \hfill \cr y =3 \hfill \cr} \right.$

b)

Ta có:

$\left\{ \matrix{ x+ y = 3m + 2 \hfill \cr 3x - 2y = 11 - m \hfill \cr} \right.$ $\left\{ \matrix{ x+ y = 3m + 2 \hfill \cr 3x - 2y = 11 - m \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x=3m+2 - y \hfill \cr 3.(3m+2-y) - 2y = 11-m \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ x=3m+2 - y \hfill \cr 3.(3m+2-y) - 2y = 11-m \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x=3m+2 - y \hfill \cr -5y = 5 -10m \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ x=3m+2 - y \hfill \cr -5y = 5 -10m \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x=3m+2 - y =3m+2 -2m + 1 = m+3\hfill \cr y = 2m - 1 \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ x=3m+2 - y =3m+2 -2m + 1 = m+3\hfill \cr y = 2m - 1 \hfill \cr} \right.$

Thay vào $y^2 - 8x^2$ được:

$y^2 - 8x^2 = (2m-1)^2 - 8(m+3)^2 = -4m^2-52m + 71$

$= -(2m + 13)^2 + 240 \leq 240$ $= -(2m + 13)^2 + 240 \leq 240$

$\Rightarrow {Max}_{y^2 - 8x^2} = 240 \Leftrightarrow 2m + 13 = 0 \Leftrightarrow m = \dfrac{-13}2$ $\Rightarrow {Max}_{y^2 - 8x^2} = 240 \Leftrightarrow 2m + 13 = 0 \Leftrightarrow m = \dfrac{-13}2$

Bài 4:

Gọi số học sinh lớp 9A là X (X ∈ ℕ*)

Số cây mỗi bạn cần trồng theo kế hoạch là $\dfrac{420}X$ $\dfrac{420}X$ (cây)

Theo giả thiết ta có:

$\dfrac{420}X + 3= \dfrac{420}{X-7}$ $\dfrac{420}X + 3= \dfrac{420}{X-7}$

$\Leftrightarrow 3X^2 -21X -2940 = 0$ $\Leftrightarrow 3X^2 -21X -2940 = 0$

$\Leftrightarrow \left[ \matrix{ X = 35 \space (tm\spaceđk) \hfill \cr X = -28 \space (loại) \hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ X = 35 \space (tm\spaceđk) \hfill \cr X = -28 \space (loại) \hfill \cr} \right.$

KL....

Bài 5:

Đề thi thử vào lớp 10 môn Toán Trường THCS Bình Dương, Quảng Ninh năm 2020 (Mã 2)

a)

Vì AB, AC là tiếp tuyến tại B, C của $(O) ⇒ ∠OBA = ∠OCA = 90° ⇒ B$, C cùng thuộc đường tròn đường kính OA, hay tứ giác ABOC nội tiếp (đpcm).

b)

Theo tính chất góc tạo bởi tiếp tuyến và dây cung, ta có ∠MBN = ∠BCN (tạo bởi tiếp tuyến BA và dây cung NB của (O).

Xét △MBN và △MCB, ta có:

Góc NMB chung

∠MBN = ∠BCN

Suy ra $△MBN ∽ △MCB ⇒ \dfrac{MB}{MN} = \dfrac{MC}{MB} ⇒ MB² = MN.MC (đpcm).$ $△MBN ∽ △MCB ⇒ \dfrac{MB}{MN} = \dfrac{MC}{MB} ⇒ MB² = MN.MC (đpcm).$

c)

Vì M là trung điểm AB ⇒ MA = MB.

$MB² = MN.MC (cmt) ⇒ \dfrac{MB}{MC} = \dfrac{MN}{MB} ⇒ \dfrac{MA}{MC} = \dfrac{MN}{MA}$ $MB² = MN.MC (cmt) ⇒ \dfrac{MB}{MC} = \dfrac{MN}{MB} ⇒ \dfrac{MA}{MC} = \dfrac{MN}{MA}$

Xét △MAN và △MCA, ta có:

Góc AMN chung

$\dfrac{MA}{MC} = \dfrac{MN}{MA}$ $\dfrac{MA}{MC} = \dfrac{MN}{MA}$

Suy ra $△MAN ∽ △MCA ⇒ ∠MAN = ∠NCA.$

Lại có $∠NCA = ∠NDC$ (t/c góc tạo bởi tiếp tuyến và dây cung)

Suy ra $∠MAN = ∠NDC = ∠ADC (đpcm).$

Đề thi thử vào lớp 10 môn Toán Trường THCS Bình Dương, Quảng Ninh năm 2020 (Mã 2) được VnDoc chia sẻ trên đây với 5 câu hỏi tự luận với thời gian 120 phút kèm theo đáp án, giúp các bạn học sinh có thêm tài liệu ôn tập chuẩn bị tốt cho kì thi sắp tới. Ngoài đề thi thử của Trường THCS Bình Dương các bạn tham khảo các đề của các tỉnh khác nữa nhé

............................................

Ngoài Đề thi thử vào lớp 10 môn Toán Trường THCS Bình Dương, Quảng Ninh năm 2020 (Mã 2). Mời các bạn học sinh còn có thể tham khảo các đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề Thi vào lớp 10 năm 2020 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt

Chia sẻ, đánh giá bài viết

1

378

Bài trước

Bài sau