Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Đề thi thử vào lớp 10 môn Toán Phòng GD&ĐT Tuy Phước, Bình Định năm 2020

Đề tuyển sinh vào 10 môn Toán năm 2020 có đáp án

Bài trước

Bài sau

Đề thi vào lớp 10 môn Toán Phòng GD&ĐT Tuy Phước năm 2020

Đề thi thử vào lớp 10 môn Toán Phòng GD&ĐT Tuy Phước, Bình Định năm 2020 được thư viện đề thi VnDoc sưu tầm và đăng tải. Đề thi vào lớp 10 môn Toán này sẽ giúp các bạn học sinh tự ôn luyện và hệ thống lại kiến thức, chuẩn bị tốt cho ôn thi vào lớp 10 các trường THPT sắp tới. Mời các bạn tham khảo.

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 9, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 9 sau: Nhóm Tài liệu học tập lớp 9. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Bài 1: (2,0 điểm)

1. Rút gọn biểu thức:

$\sqrt {54} + 2 \sqrt{24} - \sqrt{150}$ $\sqrt {54} + 2 \sqrt{24} - \sqrt{150}$

2. Cho biểu thức:

$M = \left( 1+ \dfrac{\sqrt a}{a+1} \right): \left( \dfrac{1}{\sqrt a-1} - \dfrac{2\sqrt a}{a\sqrt a+\sqrt a -a-1} \right)$ $M = \left( 1+ \dfrac{\sqrt a}{a+1} \right): \left( \dfrac{1}{\sqrt a-1} - \dfrac{2\sqrt a}{a\sqrt a+\sqrt a -a-1} \right)$

Với $a \geq 0; a ≠ 1$ $a \geq 0; a ≠ 1$

a. Rút gọn biểu thức M.

b. Tìm các giá trị của a sao cho M > 1.

Bài 2: (1,5 điểm) Cho phương trình (ẩn x, m là tham số)

$(m-1) x^2 - 2(m+1)x + m = 0$

a. Giải phương trình khi m = 2.

b. Tìm m sao cho phương trình có 2 nghiệm $x1,x2$ phân biệt thoả mãn điều kiện sau: $|x_1-x_2| \geq 2$ $|x_1-x_2| \geq 2$

Bài 3: (1,5 điểm) Một ô tô dự định đi từ tỉnh A đến tỉnh B cách nhau 120 km trong một thời gian quy định. Sau khi đi được một giờ, ô tô bị chắn đường bởi xe hoả 10 phút. Do đó, để đến tỉnh B đúng hạn, xe phải tăng vận tốc thêm 6km/h. Tính vận tốc ô tô lúc đầu.

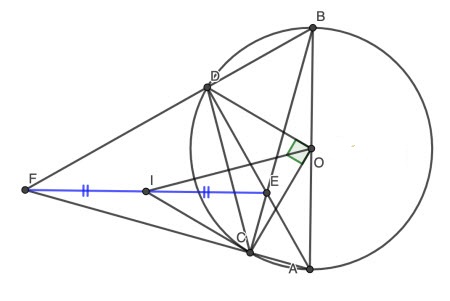
Bài 4: (4,0 điểm) Cho nửa đường tròn tâm O, đường kính AB = 2R. C là điểm nằm bất kỳ trên nửa đường tròn sao cho C ≠ A,B và AC < CB. D thuộc cung BC sao cho ∠DOC = 90°. E là giao điểm của AD và BC, F là giao điểm của AC và BD.

a. Chứng minh tứ giác CEDF là tứ giác nội tiếp.

b. Chứng minh rằng FC.FA = FD.FB.

c. I là trung điểm của EF. Chứng minh rằng IC là tiếp tuyến của (O).

d. Khi C thay đổi thoả mãn điều kiện của bài toán thì I thuộc đường tròn cố định nào?

Bài 5: (1,0 điểm) Cho a,b,c là các số thực dương. Chứng minh rằng:

$\dfrac{1}{a+2b+c} + \dfrac{1}{b+2c+a} + \dfrac{1}{c+2a+b} \leq \dfrac{1}{a+3b} + \dfrac{1}{b+3c} + \dfrac{1}{c+3a}$ $\dfrac{1}{a+2b+c} + \dfrac{1}{b+2c+a} + \dfrac{1}{c+2a+b} \leq \dfrac{1}{a+3b} + \dfrac{1}{b+3c} + \dfrac{1}{c+3a}$

Hết

Trên đây là 5 câu hỏi trong đề thi thử tuyển sinh vào lớp 10 mới nhất của Tuy Phước (Bình Định) với môn Toán, cùng làm bài thi này trong 120 phút rồi đối chiếu với đáp án chi tiết dưới đây em nhé:

Đáp án đề thi thử vào lớp 10 môn Toán năm 2020 Phòng GD&ĐT Tuy Phước

Bài 1:

$\sqrt {54} + 2 \sqrt{24} - \sqrt{150}$ $\sqrt {54} + 2 \sqrt{24} - \sqrt{150}$

$= 3\sqrt {6} + 4 \sqrt{6} - 5\sqrt{6} = 2\sqrt{6}$ $= 3\sqrt {6} + 4 \sqrt{6} - 5\sqrt{6} = 2\sqrt{6}$

Với a \geq 0; a ≠ 1, ta có:

$= \dfrac{a+\sqrt a+1}{a+1} : \left( \dfrac{1}{\sqrt a-1} - \dfrac{2\sqrt a}{(\sqrt a-1)(a+1)} \right)$ $= \dfrac{a+\sqrt a+1}{a+1} : \left( \dfrac{1}{\sqrt a-1} - \dfrac{2\sqrt a}{(\sqrt a-1)(a+1)} \right)$

$= \dfrac{a+\sqrt a+1}{a+1} :\dfrac{a+1-2\sqrt a}{(\sqrt a-1)(a+1)}$ $= \dfrac{a+\sqrt a+1}{a+1} :\dfrac{a+1-2\sqrt a}{(\sqrt a-1)(a+1)}$

$= \dfrac{a+\sqrt a+1}{a+1} .\dfrac{(\sqrt a-1)(a+1)}{(\sqrt a -1)^2}$ $= \dfrac{a+\sqrt a+1}{a+1} .\dfrac{(\sqrt a-1)(a+1)}{(\sqrt a -1)^2}$

$= \dfrac{a+\sqrt a+1}{\sqrt a-1}$ $= \dfrac{a+\sqrt a+1}{\sqrt a-1}$

Với $a \geq 0; a ≠ 1$ $a \geq 0; a ≠ 1$, ta có:

$M > 1 \Leftrightarrow \dfrac{a+\sqrt a+1}{\sqrt a-1} > 1$ $M > 1 \Leftrightarrow \dfrac{a+\sqrt a+1}{\sqrt a-1} > 1$

$\Leftrightarrow \dfrac{a+\sqrt a+1- \sqrt a+1}{\sqrt a-1} > 0$ $\Leftrightarrow \dfrac{a+\sqrt a+1- \sqrt a+1}{\sqrt a-1} > 0$

$\Leftrightarrow \dfrac{a+2}{\sqrt a-1} > 0$ $\Leftrightarrow \dfrac{a+2}{\sqrt a-1} > 0$

$\Leftrightarrow a>1$ $\Leftrightarrow a>1$

Bài 2:

Với m = 2 thay vào phương trình ta có:

$(2-1) x^2 - 2(2+1)x + 2 = 0$ $\Leftrightarrow x^2 - 6x + 2 = 0$ $\Leftrightarrow x^2 - 6x + 2 = 0$

$\Leftrightarrow \left[ \matrix{ x = 3 +\sqrt 7 \hfill \cr {x} = 3 -\sqrt 7 \hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ x = 3 +\sqrt 7 \hfill \cr {x} = 3 -\sqrt 7 \hfill \cr} \right.$

Để phương trình đã cho có 2 nghiệm phân biệt khi và chỉ khi:

$\left\{ \matrix{ \Delta$ $\left\{ \matrix{ \Delta' = (m+1)^2 - m(m-1) =3m+1 >0 \hfill \cr m-1 ≠0 \hfill \cr} \right. \Leftrightarrow m >\dfrac{-1}3;m ≠1$

Áp dụng hệ thức Vi-ét, ta có:

$\left\{ \matrix{ x_1+x_2 = \dfrac{2(m+1)}{m-1} \hfill \cr x_1x_2 = \dfrac{m}{m-1} \hfill \cr} \right.$ $\left\{ \matrix{ x_1+x_2 = \dfrac{2(m+1)}{m-1} \hfill \cr x_1x_2 = \dfrac{m}{m-1} \hfill \cr} \right.$

Ta có: $|x_1-x_2| \geq 2$ $|x_1-x_2| \geq 2$

$\Leftrightarrow (x_1-x_2)^2 \geq 4 \Leftrightarrow (x_1+x_2)^2 - 4x_1x_2 \geq 4$ $\Leftrightarrow (x_1-x_2)^2 \geq 4 \Leftrightarrow (x_1+x_2)^2 - 4x_1x_2 \geq 4$

$\Leftrightarrow \dfrac{4(m+1)^2}{(m-1)^2} - \dfrac{4m}{m-1} \geq 4$ $\Leftrightarrow \dfrac{4(m+1)^2}{(m-1)^2} - \dfrac{4m}{m-1} \geq 4$

$\Leftrightarrow \dfrac{4(m+1)^2 - 4m(m-1)}{(m-1)^2} \geq 4$ $\Leftrightarrow \dfrac{4(m+1)^2 - 4m(m-1)}{(m-1)^2} \geq 4$

$\Leftrightarrow 12m+4 \geq 4{(m-1)^2}$ $\Leftrightarrow 12m+4 \geq 4{(m-1)^2}$

$\Leftrightarrow 4m^2 - 20m \leq 0$ $\Leftrightarrow 4m^2 - 20m \leq 0$

$\Leftrightarrow m(m-5) \leq 0$ $\Leftrightarrow m(m-5) \leq 0$

$\Leftrightarrow 0 \leq m \leq 5$ $\Leftrightarrow 0 \leq m \leq 5$

Kết luận: $0 \leq m \leq 5 ; m≠1 .....$ $0 \leq m \leq 5 ; m≠1 .....$

Bài 3:

Gọi vận tốc ô tô ban đầu là $X (km/h, X > 0)$

Thời gian quy định ban đầu là $\dfrac{120}X (h)$ $\dfrac{120}X (h)$

Quãng đường ô tô đó đi được trong một giờ đầu là $1.X = X (km)$

Theo giả thiết ta có:

$\dfrac{120}X = 1 + \dfrac{10}{60} + \dfrac{120-X}{X+6}$ $\dfrac{120}X = 1 + \dfrac{10}{60} + \dfrac{120-X}{X+6}$

$\Leftrightarrow 120(X+6) = \dfrac{7}6 X(X+6)+ (120-X)X$ $\Leftrightarrow 120(X+6) = \dfrac{7}6 X(X+6)+ (120-X)X$

$\Leftrightarrow \dfrac{1}6 X^2 + 7X - 720 = 0$ $\Leftrightarrow \dfrac{1}6 X^2 + 7X - 720 = 0$

$\Leftrightarrow \left[ \matrix{ X = 48 \hfill \cr X = -90 \space (loại)\hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ X = 48 \hfill \cr X = -90 \space (loại)\hfill \cr} \right.$

KL.......

Bài 4:

Đề thi thử vào lớp 10 môn Toán Phòng GD&ĐT Tuy Phước, Bình Định năm 2020

Vì AB là đường kính của đường tròn $(O) ⇒ ∠ACB = ∠ADB = 90°$ hay $∠ECF = ∠EDF = 90°$

⇒ C, D cùng thuộc đường tròn đường kính EF, hay tứ giác CEDF nội tiếp (đpcm).

Vì tứ giác ABDC nội tiếp $⇒ ∠ABD = 180° - ∠ACD = ∠FCD$ hay $∠FBA = ∠FCD.$

Xét △FCD và △FBA, có:

Góc CFD chung

$∠FBA = ∠FCD (cmt)$

Suy ra $△FCD ∽ △FBA ⇒ \dfrac {FC}{FD} = \dfrac {FB}{FA} ⇒ FC.FA = FD.FB (đpcm).$ $△FCD ∽ △FBA ⇒ \dfrac {FC}{FD} = \dfrac {FB}{FA} ⇒ FC.FA = FD.FB (đpcm).$

Vì tứ giác CEDF nội tiếp ⇒ ∠FEC = ∠FDC (góc nội tiếp cùng chắn cung FC) = 180° - ∠CDB = ∠CAB.

Xét △FCE và △BCA, có:

∠FCE = ∠BCA (= 90°)

∠FEC = ∠CAB (cmt)

Suy ra $△FCE ∽ △BCA ⇒ ∠EFC = ∠ABC = ∠OCB$ (vì △OCB cân tại O) (1)

Xét △FCE vuông tại C, có CI là trung tuyến $⇒ CI = IE ⇒ △CIE$ cân tại I

$⇒ ∠ICE = ∠IEC (2)$

Từ (1) với (2) ta có: $∠ICE + ∠OCB = ∠IEC + ∠EFC$

$⇔ ∠ICO = 90°$ Hay IC là tiếp tuyến tại C của (O;R) (đpcm).

Chứng minh tương tự, ta có ID cũng là tiếp tuyến tới (O).

Theo tính chất tiếp tuyến ta có IC = ID và $∠ICO = ∠IDO = ∠DOC = 90° ⇒ ICOD$ là hình vuông.

$⇒ IO = \sqrt 2 OC = R\sqrt 2.$ $⇒ IO = \sqrt 2 OC = R\sqrt 2.$

Vậy khi C thay đổi thoả mãn đk bài toán thì I thuộc đường tròn $(O;R\sqrt 2).$ $(O;R\sqrt 2).$

Bài 5:

Ta áp dụng BĐT AM-GM cho x,y dương:

$(x+y)^2 \geq 4 xy$ $(x+y)^2 \geq 4 xy$

$\Leftrightarrow (x+y)\left(\dfrac{x+y}{xy} \right) \geq 4$ $\Leftrightarrow (x+y)\left(\dfrac{x+y}{xy} \right) \geq 4$

$\Leftrightarrow \dfrac{1}{x} + \dfrac{1}{y} \geq \dfrac{4}{x+y} (*)$ $\Leftrightarrow \dfrac{1}{x} + \dfrac{1}{y} \geq \dfrac{4}{x+y} (*)$

Áp dụng (*), ta có:

$\dfrac{1}{a+3b} + \dfrac{1}{a+b+2c} \geq \dfrac{4}{2a+4b+2c} =\dfrac{2}{a+2b+c}$ $\dfrac{1}{a+3b} + \dfrac{1}{a+b+2c} \geq \dfrac{4}{2a+4b+2c} =\dfrac{2}{a+2b+c}$

Chứng minh tương tự ta có:

$\dfrac{1}{b+3c} + \dfrac{1}{2a+b+c} \geq \dfrac{4}{2a+2b+4c} =\dfrac{2}{a+b+2c}$ $\dfrac{1}{b+3c} + \dfrac{1}{2a+b+c} \geq \dfrac{4}{2a+2b+4c} =\dfrac{2}{a+b+2c}$

$\dfrac{1}{c+3a} + \dfrac{1}{a+2b+c} \geq \dfrac{4}{4a+2b+2c} =\dfrac{2}{2a+b+c}$ $\dfrac{1}{c+3a} + \dfrac{1}{a+2b+c} \geq \dfrac{4}{4a+2b+2c} =\dfrac{2}{2a+b+c}$

Cộng vế theo vế đồng thời khử hạng tử trùng lặp của 3 BĐT trên, ta có:

$\dfrac{1}{a+3b} + \dfrac{1}{b+3c} + \dfrac{1}{c+3a} \geq \dfrac{1}{a+2b+c} + \dfrac{1}{b+2c+a} + \dfrac{1}{c+2a+b} (đpcm)$ $\dfrac{1}{a+3b} + \dfrac{1}{b+3c} + \dfrac{1}{c+3a} \geq \dfrac{1}{a+2b+c} + \dfrac{1}{b+2c+a} + \dfrac{1}{c+2a+b} (đpcm)$

Dấu bằng xảy ra khi và chỉ khi a = b = c.

Đề thi thử vào lớp 10 môn Toán Phòng GD&ĐT Tuy Phước, Bình Định năm 2020 được VnDoc chia sẻ trên đây với 5 câu hỏi tự luận với thời gian 120 phút, giúp các bạn học sinh có thêm tài liệu ôn tập chuẩn bị tốt cho kì thi sắp tới. Ngoài đề thi thử của Phòng GD&ĐT Tuy Phước các bạn tham khảo các đề của các tỉnh khác nữa nhé