Đề thi tham khảo vào lớp 10 môn Toán Sở GD&ĐT Tây Ninh năm học 2020 - 2021

Đề thi tham khảo vào lớp 10 môn Toán 2020 có đáp án

Đề thi tham khảo vào lớp 10 môn Toán Sở GD&ĐT Tây Ninh năm 2020

Đề thi tham khảo vào lớp 10 môn Toán Sở GD&ĐT Tây Ninh năm học 2020 - 2021 được VnDoc sưu tầm và đăng tải. Tài liệu giúp các bạn học sinh củng cố lại phần kiến thức đã học và kỹ năng giải đề thi, biết cách phân bổ thời gian làm bài sao cho hợp lý. Mời các bạn cùng tham khảo

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 9, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 9 sau: Nhóm Tài liệu học tập lớp 9. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Đề thi minh họa vào lớp 10 môn Toán tỉnh Tây Ninh

Câu 1:(1,0 điểm)

Tính giá trị biểu thức $S = \sqrt{36} – \sqrt{9} + \sqrt{16}$ $S = \sqrt{36} – \sqrt{9} + \sqrt{16}$

Câu 2:(1,0 điểm)

Tìm x để biểu thức $T= \sqrt{3x-2}$ $T= \sqrt{3x-2}$ xác định.

Câu 3:(1,0 điểm)

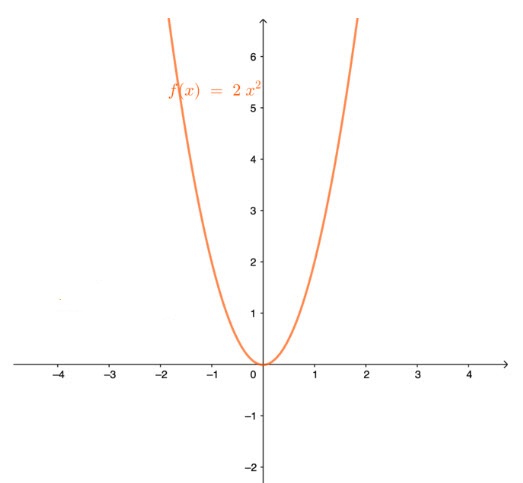
Vẽ đồ thị của hàm số $y = 2x².$

Câu 4:(1,0 điểm)

Tìm m để đường thẳng $d: y = mx + 2m -3$ đi qua điểm A(0;5).

Câu 5:(1,0 điểm)

Giải hệ phương trình

$\left\{ \matrix{ 2x + y = 1 \hfill \cr 3x – 2y = 12 \hfill \cr} \right.$ $\left\{ \matrix{ 2x + y = 1 \hfill \cr 3x – 2y = 12 \hfill \cr} \right.$

Câu 6:(1,0 điểm)

Cho hình thoi ABCD có AC = a, BD= 3a. Tính độ dài AB theo a.

Câu 7:(1,0 điểm)

Một mảnh vườn hình chữ nhật có chu vi bằng 28 m và độ dài đường chéo bằng 5/4 lần chiều dài của mảnh vườn đó. Tính diện tích của mảnh vườn đã cho.

Câu 8:(1,0 điểm)

Tìm a và b để đường thẳng $d1: y = ax+b$ cắt đường thẳng $d2, y = bx-a$ tại điểm M(2;1)

Câu 9:(1,0 điểm)

Cho tam giác ABC ( AC > AB) và ∠BAC = 60°. Trên cạnh AC lấy điểm D sao cho CD = AB. Gọi M, N lần lượt là trung điểm của AD và BC. Tính ∠CMN

Câu 10:(1,0 điểm)

Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của AB và AD, BN cắt CM tại P. Tính tỉ số giữa diện tích tam giác BMP và diện tích hình bình hành ABCD.

- Hết -

Đáp án đề thi thử Toán vào 10 Tây Ninh năm 2020

Câu 1:

$S = \sqrt{36} – \sqrt{9} + \sqrt{16} =6-3+4 =7$ $S = \sqrt{36} – \sqrt{9} + \sqrt{16} =6-3+4 =7$

Câu 2:

Để biểu thức $T= \sqrt{3x-2}$ $T= \sqrt{3x-2}$ xác định

$\Leftrightarrow 3x-2 \geq 0 \Leftrightarrow x\geq \dfrac{2}3$ $\Leftrightarrow 3x-2 \geq 0 \Leftrightarrow x\geq \dfrac{2}3$

Câu 3:

Các em cần kẻ bảng tọa độ điểm rồi tiến hành vẽ:

Đề thi tham khảo vào lớp 10 môn Toán Sở GD&ĐT Tây Ninh năm học 2020 - 2021

Câu 4:

Để A thuộc (d) thì toạ độ điểm A phải thoả mãn phương trình (d):

5 = m.0 + 2m - 3

$\Leftrightarrow m = 4$ $\Leftrightarrow m = 4$

Câu 5:

$\left\{ \matrix{ 2x + y = 1 \hfill \cr 3x – 2y = 12 \hfill \cr} \right.$ $\left\{ \matrix{ 2x + y = 1 \hfill \cr 3x – 2y = 12 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x=2 \hfill \cr y=-3 \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ x=2 \hfill \cr y=-3 \hfill \cr} \right.$

Câu 6:

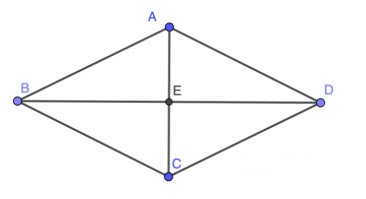
Đề thi tham khảo vào lớp 10 môn Toán Sở GD&ĐT Tây Ninh năm học 2020 - 2021

Gọi E là giao của AC và BD. Theo tính chất hình thoi ta có: AE = EC và DE = EB.

Áp dụng định lý Pytago cho △ABE vuông tại E, ta có:

$AB = \sqrt{{AE}^2 + {EB}^2} = \sqrt{{\left(\dfrac{AC}2\right)}^2 + {\left(\dfrac{BD}2\right)}^2} =\sqrt{{\left(\dfrac{a}2\right)}^2 + {\left(\dfrac{3a}2\right)}^2} = \dfrac{a\sqrt{10}}2$ $AB = \sqrt{{AE}^2 + {EB}^2} = \sqrt{{\left(\dfrac{AC}2\right)}^2 + {\left(\dfrac{BD}2\right)}^2} =\sqrt{{\left(\dfrac{a}2\right)}^2 + {\left(\dfrac{3a}2\right)}^2} = \dfrac{a\sqrt{10}}2$

Câu 7:

Gọi chiều dài và rộng của mảnh vườn đó lần lượt là A và B (mét, A,B > 0)

Độ dài đường chéo mảnh vườn là $\sqrt{A^2+B^2} (m)$ $\sqrt{A^2+B^2} (m)$

Theo bài ra ta có hệ:

$\left\{ \matrix{ 2A+2B = 28 \hfill \cr \sqrt{A^2+B^2} = \dfrac{5}4 A \hfill \cr} \right.$ $\left\{ \matrix{ 2A+2B = 28 \hfill \cr \sqrt{A^2+B^2} = \dfrac{5}4 A \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ A + B = 14 \hfill \cr A^2 +B^2 = \dfrac{25}{16} A^2 \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ A + B = 14 \hfill \cr A^2 +B^2 = \dfrac{25}{16} A^2 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ A + B = 14 \hfill \cr B^2 = \dfrac{9}{16} A^2 \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ A + B = 14 \hfill \cr B^2 = \dfrac{9}{16} A^2 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ A + B = 14 \hfill \cr B = \dfrac{3}{4} A \hfill \cr} \right. (vì A,B > 0)$ $\Leftrightarrow \left\{ \matrix{ A + B = 14 \hfill \cr B = \dfrac{3}{4} A \hfill \cr} \right. (vì A,B > 0)$

$\Leftrightarrow \left\{ \matrix{ A = 8 \hfill \cr B = 6 \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ A = 8 \hfill \cr B = 6 \hfill \cr} \right.$

KL....

Câu 8:

Để d1 và d2 cắt nhau tại M(2;1) tức là toạ độ điểm M thoả mãn phương trình của d1 và d2:

$\left\{ \matrix{ 1=2a+b \hfill \cr 1=2b-a \hfill \cr} \right.$ $\left\{ \matrix{ 1=2a+b \hfill \cr 1=2b-a \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ a = \dfrac{1}5 \hfill \cr b = \dfrac{3}5 \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ a = \dfrac{1}5 \hfill \cr b = \dfrac{3}5 \hfill \cr} \right.$

Câu 9:

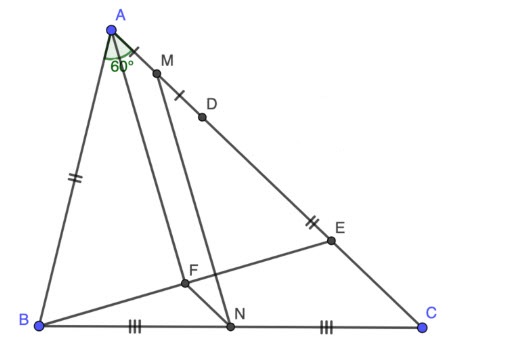
Đề thi tham khảo vào lớp 10 môn Toán Sở GD&ĐT Tây Ninh năm học 2020 - 2021

Trên AC lấy điểm E sao cho $AE = AB = DC ⇒ AD + DE = DE + EC ⇒ AD = EC.$

△AEB cân tại A, có $∠BAC = 60° ⇒ △AEB$ đều.

Lấy F là trung điểm BE, xét △CBE có F là trung điểm BE, N là trung điểm BC

⇒ FN là đường trung bình $⇒ FN // EC và FN = \dfrac{1}2 EC = \dfrac{1}2 AD = AM$ $⇒ FN // EC và FN = \dfrac{1}2 EC = \dfrac{1}2 AD = AM$

Ta có $FN // AM, FN = AM ⇒ AMNF$ là hình bình hành ⇒ MN // AF

Suy ra $∠CMN = ∠CAF = \dfrac{1}2 \angle BAC = 30°.$ $∠CMN = ∠CAF = \dfrac{1}2 \angle BAC = 30°.$

Câu 10:

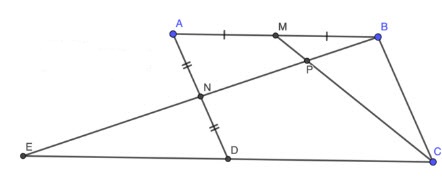
Đề thi tham khảo vào lớp 10 môn Toán Sở GD&ĐT Tây Ninh năm học 2020 - 2021

Vì M là trung điểm AB

⇒ $MB = \dfrac{1}2 AB ⇒ S_{CMB} = \dfrac{1}2 S_{CAB} = \dfrac{1}4 S_{ABCD}$ $MB = \dfrac{1}2 AB ⇒ S_{CMB} = \dfrac{1}2 S_{CAB} = \dfrac{1}4 S_{ABCD}$ (cùng độ dài chiều cao)

Kéo dài BN cắt CD tại E.

Dễ thấy $EC = 2ED = 2DC.$

Xét △PMB và △PCE, ta có:

$∠EPC = ∠BPM$ (đối đỉnh)

$∠PMB = ∠PCE$(so le trong)

Suy ra $△PMB ∽ △PCE ⇒ \dfrac{PM}{PC} = \dfrac{MB}{EC} = \dfrac{1}{4} ⇒ \dfrac{PM}{MC} = \dfrac{1}{5}$ $△PMB ∽ △PCE ⇒ \dfrac{PM}{PC} = \dfrac{MB}{EC} = \dfrac{1}{4} ⇒ \dfrac{PM}{MC} = \dfrac{1}{5}$

Suy ra $MP = \dfrac{1}5 MC$ $MP = \dfrac{1}5 MC$

$⇒ S_{BMP} = \dfrac{1}5S_{BMC} = \dfrac{1}5 . \dfrac{1}4 S_{ABCD} = \dfrac{1}{20} S_{ABCD}$ $⇒ S_{BMP} = \dfrac{1}5S_{BMC} = \dfrac{1}5 . \dfrac{1}4 S_{ABCD} = \dfrac{1}{20} S_{ABCD}$ .

Đề thi tham khảo vào lớp 10 môn Toán Sở GD&ĐT Tây Ninh năm học 2020 - 2021 được VnDoc chia sẻ trên đây là tài liệu hay, giúp các bạn học sinh có thêm tài liệu ôn tập chuẩn bị tốt cho kì thi sắp tới

............................................

Ngoài Đề thi tham khảo vào lớp 10 môn Toán Sở GD&ĐT Tây Ninh năm học 2020 - 2021. Mời các bạn học sinh còn có thể tham khảo các đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề Thi vào lớp 10 năm 2019 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt

Chia sẻ, đánh giá bài viết

1

1.821

Bài trước

Bài sau