Đề thi thử vào 10 môn Toán Sở GD&ĐT Ninh Bình năm học 2020 - 2021 (lần 2)

Đề tuyển sinh vào lớp 10 môn Toán có đáp án

Đề thi thử vào lớp 10 môn Toán Sở GD&ĐT Ninh Bình năm 2020

Đề thi thử vào 10 môn Toán Sở GD&ĐT Ninh Bình năm học 2020 - 2021 (lần 2) được VnDoc chia sẻ nằm trong bộ tài liệu đề thi thử vào lớp 10. Hy vọng với tài liệu này các bạn học sinh sẽ có thêm tài liệu ôn tập tại nhà, đồng thời chuẩn bị tốt cho kì thi sắp tới. Chúc các bạn học tốt

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 9, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 9 sau: Nhóm Tài liệu học tập lớp 9. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

SỞ GD&ĐT NINH BÌNH

(Đề thi có 01 trang)

ĐỀ THI THỬ VÀO LỚP 10 THPT

LẦN THỨ HAI - NĂM HỌC 2019 - 2020;

MÔN TOÁN

Thời gian làm bài: 120 phút, không kể thời gian nhất để

Câu 1 (1,5 điểm)

a) Tìm điều kiện của x để biểu thức $A = \sqrt{x – 2020}$ $A = \sqrt{x – 2020}$ có nghĩa.

b) Rút gọn biểu thức $B = \dfrac{1}{\sqrt{7}+2} + \dfrac{1}{\sqrt{7}-2}$ $B = \dfrac{1}{\sqrt{7}+2} + \dfrac{1}{\sqrt{7}-2}$

Câu 2 (2,5 điểm).

1, Bằng phép toán, hãy xác định tọa độ giao điểm của parabol y = x² và đường thẳng y = 5x - 4.

2. Cho phương trình bậc hai $5x² -8x +1= 0$. Biết phương trình có hai nghiệm phân biệt $x_1, x_2$. Không giải phương trình, hãy tính giá trị các biểu thức sau .

$a)\ x_1.x_2 + 2(x_1 + x_2)$ $a)\ x_1.x_2 + 2(x_1 + x_2)$

$b)\ \dfrac{x_1}{x_2} + \dfrac{x_2}{x_1}$ $b)\ \dfrac{x_1}{x_2} + \dfrac{x_2}{x_1}$

Câu 3 (1,5 điểm). Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình

Người ta hòa lẫn 5 lít chất lỏng A với 7 lít chất lỏng B thì được một hỗn hợp có khối lượng bằng 5 kg. Biết các thành phần trong hai chất lỏng không có phản ứng hóa học với nhau và khối lượng riêng của chất lỏng B lớn hơn khối lượng riêng của chất lỏng A là 0,2 kg/dm³. Tính khối lượng riêng của mỗi chất lông A và B.

Câu 4 (3,5 điểm).

1. Cho đường tròn tâm O. Qua điểm C nằm ngoài đường tròn vẽ các tiếp tuyển CD, CE với đường tròn (D và E là các tiếp điểm). Gọi H là giao điểm của DE với CO, I là giao điểm của đoạn thẳng CO với đường tròn. Chứng minh rằng:

a) Tứ giác CDOE là tứ giác nội tiếp.

b) IC.DH = IH.DC.

2. Người ta thả từ từ một quả cầu đặc bằng sắt vào một cái thùng đựng đầy nước thì thấy quả cầu chìm hoàn toàn trong nước và lượng nước tràn ra bằng 113,04 lít. Tính bán kính của quả cầu (lấy π = 3,14).

Câu 5 (1,0 điểm).

a) Cho a, b, c là các số thực dương thỏa mãn $ab + bc+ca= 3abc$. Tìm giá trị lớn nhất của biểu thức

$P = \dfrac{1}{a+2b} + \dfrac{1}{b+2c} + \dfrac{1}{c+2a}$ $P = \dfrac{1}{a+2b} + \dfrac{1}{b+2c} + \dfrac{1}{c+2a}$

b) Có bao nhiêu số tự nhiên có 10 chữ số được tạo thành từ các chữ số 1, 2, 3 sao cho bất kì hai chữ số nào đứng cạnh nhau trong số tự nhiên đó cũng hơn kém nhau 1 đơn vị?

Hết

Đáp án đề thi thử vào 10 môn Toán Sở GD&ĐT Ninh Bình năm 2020

Câu 1 (1,5 điểm)

$a)\ x ≥ 2020$ $a)\ x ≥ 2020$

$b)\ B = \dfrac{2\sqrt{7}}{3}$ $b)\ B = \dfrac{2\sqrt{7}}{3}$

Câu 2 (2,5 điểm).

$1. (1 ; 1), (4 ; 16)$

2. Áp dụng Vi-et

$\left\{ \matrix{ x_1 . x_2 = \dfrac{8}{5} \hfill \cr x_1 + x_2 = \dfrac{1}{5} \hfill \cr} \right.$ $\left\{ \matrix{ x_1 . x_2 = \dfrac{8}{5} \hfill \cr x_1 + x_2 = \dfrac{1}{5} \hfill \cr} \right.$

$a) x_1. x_2 + 2(x_1 + x_2) =\dfrac{17}{5}$ $a) x_1. x_2 + 2(x_1 + x_2) =\dfrac{17}{5}$

$b)\ \dfrac{x_1}{x_2} + \dfrac{x_2}{x_1} = \dfrac{54}{5}$ $b)\ \dfrac{x_1}{x_2} + \dfrac{x_2}{x_1} = \dfrac{54}{5}$

Câu 3. 1.5 điểm

Đổi 5 lít = 5dm³,7 lít = 7dm³.

Gọi khối lượng riêng của chất lỏng A và chất lỏng B lần lượt là x và y (kg/dm³, x>0, y > 0,2).(Nếu học sinh chỉ đặt điều kiện y>0 thì châm chước vì thật ra còn ràng buộc bởi điều kiện x>0)

Vì khối lượng riêng của chất lỏng B lớn hơn khối lượng riêng của chất lỏng A là 0,2 kg/dm³ nên ta có phương trình x = y-0,2 (1).

Khối lượng của chất lỏng A là 5x (kg), khối lượng của chất lỏng B là 7y (kg).

Vì khối lượng của hỗn hợp là 5kg nên ta có phương trình 5x +7y = 5 (2).

Kết hợp (1) và (2) ta có hệ phương trình:

$\left\{ \matrix{ x = y-0,2 \,\,(1)\hfill \cr 5x+7y = 5 \,\,(2) \hfill \cr} \right.⇔ \left\{ \matrix{ x = 0,3 \hfill \cr y = 0,5 \hfill \cr} \right.$ $\left\{ \matrix{ x = y-0,2 \,\,(1)\hfill \cr 5x+7y = 5 \,\,(2) \hfill \cr} \right.⇔ \left\{ \matrix{ x = 0,3 \hfill \cr y = 0,5 \hfill \cr} \right.$ (thỏa mãn).

Vậy khối lượng riêng của chất lỏng A và chất lỏng B lần lượt là 0,3 kg/dm³ và 0,5 kg/dm³ .

Câu 4. 3,5 điểm.

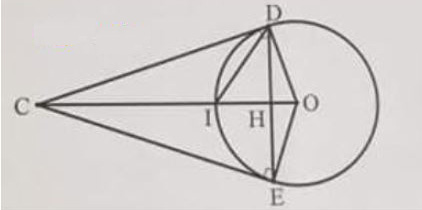
Đề thi thử vào 10 môn Toán Sở GD&ĐT Ninh Bình năm học 2020 - 2021 (lần 2)

a) (1,0 điểm)

Vi CD là tiếp tuyến của đường tròn tại D nên ∠CDO = 90° điểm)

Vi CE là tiếp tuyến của đường tròn tại E nên ∠CEO = 90°.

Tứ giác CDOE có $∠CDO + ∠CEO = 90° + 90° = 180°.$

Do đó tứ giác CDOE là tứ giác nội tiếp.

b) (1,0 điểm)

Vì CD và CE là hai tiếp tuyến của đường tròn nên theo tính chất của hai tiếp tuyến cắt nhau ta có OC là tia phân giác của góc DOE, tức là DOI = EỌI. Suy ra DI = I.

Vì CDI là góc tạo bởi tia tiếp tuyến DC và dây cung DI nên $∠CDI= \dfrac{1}{2}sd \stackrel\frown{DI}$ $∠CDI= \dfrac{1}{2}sd \stackrel\frown{DI}$

Vì ∠IDE là góc nội tiếp chắn cung EI nên $∠IDE = \dfrac{1}{2}sd \stackrel\frown{EI}.$ $∠IDE = \dfrac{1}{2}sd \stackrel\frown{EI}.$

Mà DI = EI nên suy ra ∠CDI = ∠IDE hay DI là tia phân giác của góc CDE

Áp dụng tính chất đường phân giác trong tam giác CDH ta có

$\dfrac{IC}{IH} = \dfrac{DC}{DH} ⇒ IC.DH = IH.DC$ $\dfrac{IC}{IH} = \dfrac{DC}{DH} ⇒ IC.DH = IH.DC$

2) (1,0 điểm) Gọi V (dm³) là thể tích của quả cầu và r (dm) là bán kính của quả cầu.

Ta có $V = \dfrac{4}{3}.πr³ = \dfrac{4}{3}.3,14r³ (dm³),$ $V = \dfrac{4}{3}.πr³ = \dfrac{4}{3}.3,14r³ (dm³),$

Đổi 113,04 lít = 113,04 dm³

Lượng nước tràn ra chính là thể tích của quả cầu sắt. Do đó ta có V =113,04 dm³

Do đó ta có $\dfrac{4}{3}.3,14r³ = 113,04$ $\dfrac{4}{3}.3,14r³ = 113,04$

$⇔ r³ = 27 ⇔ r = 3$

Vậy bán kính của quả cầu là 3 dm.

Câu 5 (1.0 điểm)

a) (0,5 điểm)

Ta có với mọi số thực dương thì $a_1, a_2, ..., a_n; x_1, x_2, ..., x_n$ thì:

$\dfrac{a_1^2}{x_1} + \dfrac{a_2^2}{x_2}+....+ \dfrac{a_n^2}{x_n} ≥ \dfrac{(a_1 + a_2 + ... + a_n)^2}{x_1 + x_2 + ... + x_n}$ $\dfrac{a_1^2}{x_1} + \dfrac{a_2^2}{x_2}+....+ \dfrac{a_n^2}{x_n} ≥ \dfrac{(a_1 + a_2 + ... + a_n)^2}{x_1 + x_2 + ... + x_n}$

Dấu bằng xảy ra khi $\dfrac{a_1}{x_1} = \dfrac{a_2}{x_2} = ... = \dfrac{a_n}{x_n}$ $\dfrac{a_1}{x_1} = \dfrac{a_2}{x_2} = ... = \dfrac{a_n}{x_n}$

Áp dụng, ta có:

$\dfrac{1}{a+2b} ≤ \dfrac{1}{9}\left( \dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{b} \right)$ $\dfrac{1}{a+2b} ≤ \dfrac{1}{9}\left( \dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{b} \right)$

$\dfrac{1}{b+2c} ≤ \dfrac{1}{9}\left( \dfrac{1}{b} + \dfrac{1}{c} + \dfrac{1}{c} \right)$ $\dfrac{1}{b+2c} ≤ \dfrac{1}{9}\left( \dfrac{1}{b} + \dfrac{1}{c} + \dfrac{1}{c} \right)$

$\dfrac{1}{c+2a} ≤ \dfrac{1}{9}\left( \dfrac{1}{c} + \dfrac{1}{a} + \dfrac{1}{a} \right)$ $\dfrac{1}{c+2a} ≤ \dfrac{1}{9}\left( \dfrac{1}{c} + \dfrac{1}{a} + \dfrac{1}{a} \right)$

Cộng từng về các bất đẳng thức trên ta được

$P = \dfrac{1}{a+2b} + \dfrac{1}{b+2c} + \dfrac{1}{c+2a} ≤ \dfrac{1}{9} \left(\dfrac{3}{a} + \dfrac{3}{b} + \dfrac{3}{c}\right) = \dfrac{1}{3} \left( \dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} \right)$ $P = \dfrac{1}{a+2b} + \dfrac{1}{b+2c} + \dfrac{1}{c+2a} ≤ \dfrac{1}{9} \left(\dfrac{3}{a} + \dfrac{3}{b} + \dfrac{3}{c}\right) = \dfrac{1}{3} \left( \dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} \right)$

Từ giả thiết: $ab+bc+ca = 3abc ⇔ \dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} = 3$ $ab+bc+ca = 3abc ⇔ \dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} = 3$

Do đó $P≤\dfrac{1}{3}.3=1$ $P≤\dfrac{1}{3}.3=1$. Dấu bằng xảy ra khi a = b = c =1.

Vậy giá trị lớn nhất của P bằng 1 đạt được khi a = b = c =1.

b) (0,5 điểm)

Nếu chữ số đầu tiên (tính từ trái qua phải) bằng 2: Chữ số thứ hai sẽ phải là 1 hoặc 3. Do đó chữ số thứ ba sẽ phải là chữ số 2. Cứ tiếp tục lập luận như vậy ta thấy chữ số đứng vị trí lẻ là chữ số 2, chữ số đứng ở vị trí chẵn là chữ số 1 hoặc 3. Vậy có 2 = 32 số.

Nếu chữ số đầu tiên (tính từ trái qua phải) là chữ số 1 hoặc chữ số 3: Chữ số thứ hai phải là chữ số 2. Chữ số thứ ba phải là chữ số 1 hoặc 3. Cứ tiếp tục lập luận như vậy ta thấy chữ số đứng ở vị trí lẻ là chữ số 1 hoặc 3, chữ số đứng ở vị trí chắn là chữ số 2. Vậy có 2⁵ = 32 số.

Vậy có tổng cộng 32 + 32 = 64 số.

Đề thi thử vào 10 môn Toán Sở GD&ĐT Ninh Bình năm học 2020 - 2021 (lần 2) được VnDoc chia sẻ trên đây với 5 câu hỏi tự luận, giúp các bạn học sinh có thêm tài liệu ôn tập chuẩn bị tốt cho kì thi sắp tới. Ngoài đề thi thử của tỉnh Ninh Bình các bạn tham khảo các đề của các tỉnh khác nữa nhé

............................................

Ngoài Đề thi thử vào 10 môn Toán Sở GD&ĐT Ninh Bình năm học 2020 - 2021 (lần 2). Mời các bạn học sinh còn có thể tham khảo các đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề Thi vào lớp 10 năm 2020 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt

Chia sẻ, đánh giá bài viết

1

644

Bài trước

Bài sau