Đáp án đề thi tuyển sinh lớp 10 môn Toán tỉnh Thanh Hóa năm 2020

Đáp án chính thức của Sở GD&ĐT Thanh Hóa môn Toán năm 2020

Đề thi tuyển sinh lớp 10 môn Toán Sở GD&ĐT Thanh Hóa năm 2020

Đáp án đề thi tuyển sinh lớp 10 môn Toán tỉnh Thanh Hóa năm 2020. Được VnDoc sưu tầm và đăng tải, kèm lời giải chi tiết cho các bạn đánh giá so sánh, hy vọng tài liệu này sẽ giúp ích cho các bạn học sinh ôn tập, chuẩn bị tốt cho kì thi vào lớp 10 THPT sắp tới. Mời các bạn cùng tham khảo

Lưu ý: Điểm chuẩn, điểm thi vào lớp 10 tỉnh Thanh Hóa năm 2020

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 9, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 9 sau: Nhóm Tài liệu học tập lớp 9. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Đáp án chính thức tuyển sinh lớp 10 môn Toán tỉnh Thanh Hóa năm 2020

Đáp án đề thi tuyển sinh lớp 10 môn Toán tỉnh Thanh Hóa năm 2020

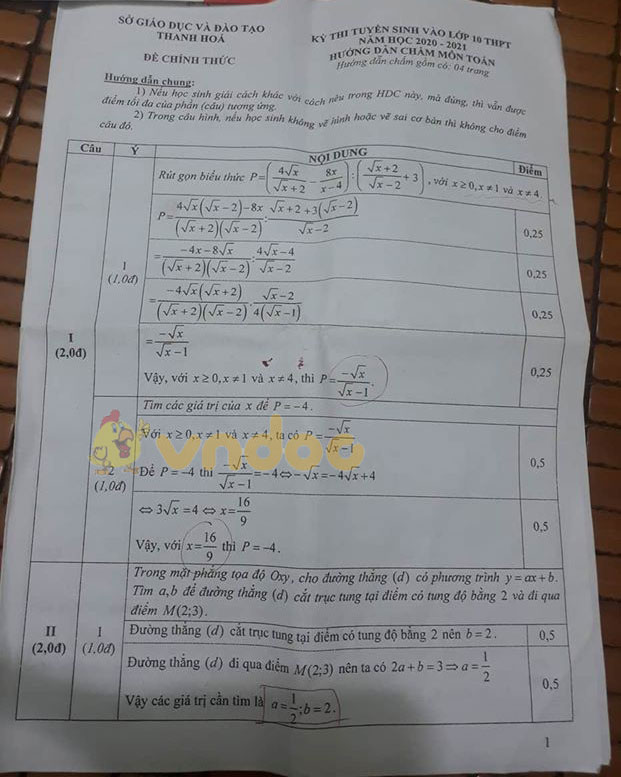
Đáp án đề thi tuyển sinh lớp 10 môn Toán tỉnh Thanh Hóa năm 2020 được đội ngũ giáo viên Vndoc giải đáp

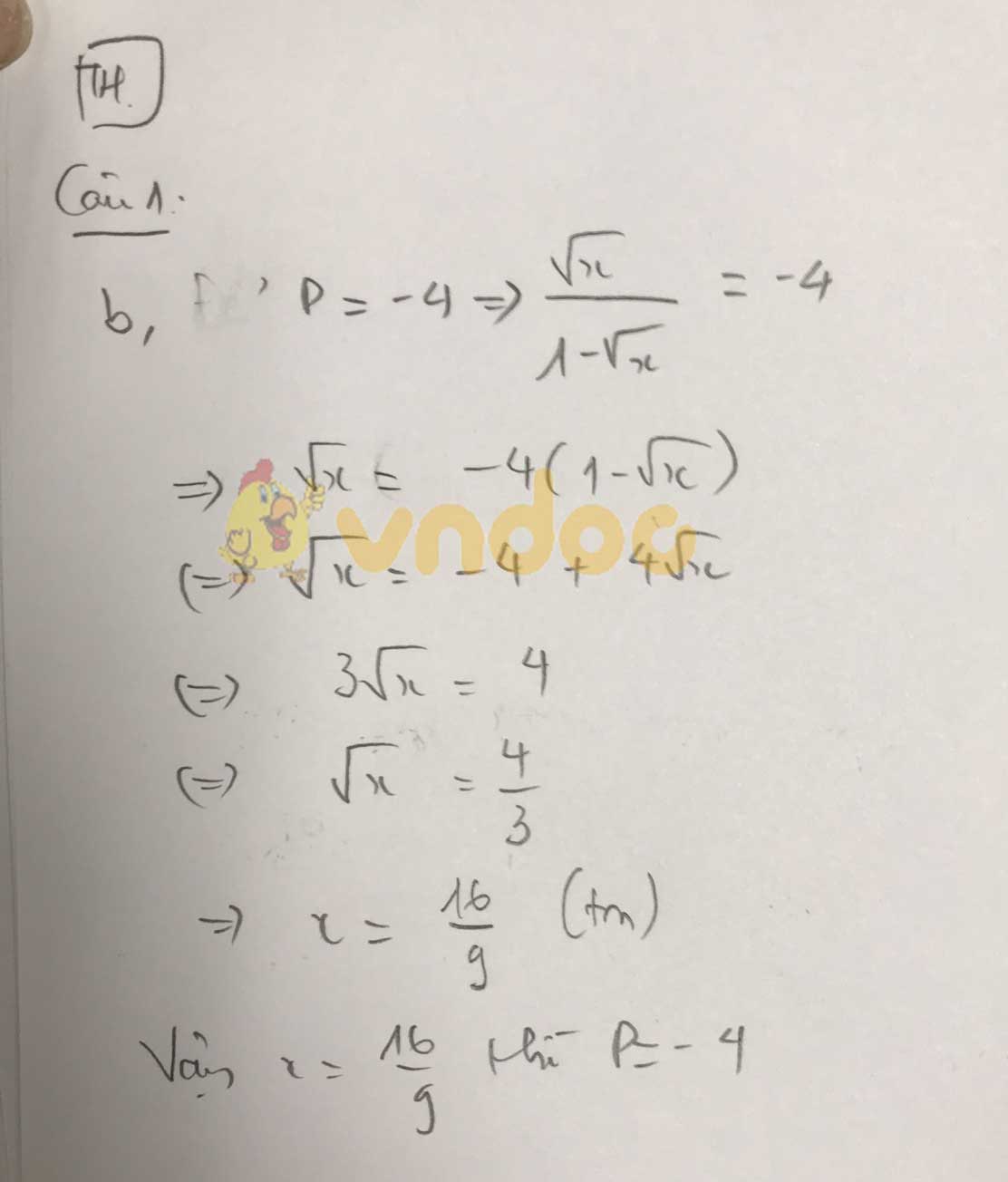
Đáp án đề thi tuyển sinh lớp 10 môn Toán tỉnh Thanh Hóa năm 2020

Câu 5

Từ $x+y+z=x y z \Rightarrow \frac{1}{x y}+\frac{1}{y z}+\frac{1}{z x}=1$ $x+y+z=x y z \Rightarrow \frac{1}{x y}+\frac{1}{y z}+\frac{1}{z x}=1$

Đặt $a=\frac{1}{x} ; b=\frac{1}{y} ; c=\frac{1}{z}(a, b, c>0)$ $a=\frac{1}{x} ; b=\frac{1}{y} ; c=\frac{1}{z}(a, b, c>0)$

Suy ra $a b+b c+c a=1$

Ta có $\frac{y+2}{x^{2}}=\frac{1}{x^{2}} \cdot(y+2)=\frac{1}{x^{2}} \frac{1+\frac{2}{y}}{\frac{1}{y}}=a^{2} \cdot \frac{1+2 b}{b}=\frac{a^{2}}{b}+2 a^{2}$ $\frac{y+2}{x^{2}}=\frac{1}{x^{2}} \cdot(y+2)=\frac{1}{x^{2}} \frac{1+\frac{2}{y}}{\frac{1}{y}}=a^{2} \cdot \frac{1+2 b}{b}=\frac{a^{2}}{b}+2 a^{2}$

Suy ra $Q=\frac{a^{2}}{b}+\frac{b^{2}}{c}+\frac{c^{2}}{a}+2\left(a^{2}+b^{2}+c^{2}\right)$ $Q=\frac{a^{2}}{b}+\frac{b^{2}}{c}+\frac{c^{2}}{a}+2\left(a^{2}+b^{2}+c^{2}\right)$

Mà $\frac{a^{2}}{b}+\frac{b^{2}}{c}+\frac{c^{2}}{a} \geq \frac{(a+b+c)^{2}}{a+b+c}=a+b+c$ $\frac{a^{2}}{b}+\frac{b^{2}}{c}+\frac{c^{2}}{a} \geq \frac{(a+b+c)^{2}}{a+b+c}=a+b+c$

Nên $Q \geq 2\left(a^{2}+b^{2}+c^{2}\right)+a+b+c$ $Q \geq 2\left(a^{2}+b^{2}+c^{2}\right)+a+b+c$

Lại có

$a^{2}+\frac{1}{3} \geq 2 \sqrt{a^{2} \cdot \frac{1}{3}}=\frac{2 a}{\sqrt{3}}=\frac{2 \sqrt{3}}{3} a$ $a^{2}+\frac{1}{3} \geq 2 \sqrt{a^{2} \cdot \frac{1}{3}}=\frac{2 a}{\sqrt{3}}=\frac{2 \sqrt{3}}{3} a$

$b^{2}+\frac{1}{3} \geq 2 \sqrt{b^{2} \cdot \frac{1}{3}}=\frac{2 b}{\sqrt{3}}=\frac{2 \sqrt{3}}{3} b$ $b^{2}+\frac{1}{3} \geq 2 \sqrt{b^{2} \cdot \frac{1}{3}}=\frac{2 b}{\sqrt{3}}=\frac{2 \sqrt{3}}{3} b$

${c^{2}}+\frac{1}{3} \geq 2 \sqrt{c^{2} \cdot \frac{1}{3}}=\frac{2 c}{\sqrt{3}}=\frac{2 \sqrt{3}}{3} c$ ${c^{2}}+\frac{1}{3} \geq 2 \sqrt{c^{2} \cdot \frac{1}{3}}=\frac{2 c}{\sqrt{3}}=\frac{2 \sqrt{3}}{3} c$

Suy ra

$a^{2}+b^{2}+c^{2}+1 \geq \frac{2 \sqrt{3}}{3}(a+b+c)$ $a^{2}+b^{2}+c^{2}+1 \geq \frac{2 \sqrt{3}}{3}(a+b+c)$

$\Rightarrow 2\left(a^{2}+b^{2}+c^{2}\right) \geq \frac{4 \sqrt{3}}{3}(a+b+c)-2$ $\Rightarrow 2\left(a^{2}+b^{2}+c^{2}\right) \geq \frac{4 \sqrt{3}}{3}(a+b+c)-2$

$\Rightarrow Q\left(\frac{4 \sqrt{3}}{3}+1\right)(a+b+c)-2$ $\Rightarrow Q\left(\frac{4 \sqrt{3}}{3}+1\right)(a+b+c)-2$

Mà

$(a+b+c)^{2} \geq 3(a b+b c+c a)=3$ $(a+b+c)^{2} \geq 3(a b+b c+c a)=3$

$\Rightarrow (a+b+c) \geq \sqrt{3}$ $\Rightarrow (a+b+c) \geq \sqrt{3}$

Vậy $Q \geq\left(\frac{4 \sqrt{3}}{3}+1\right) \sqrt{3}-2=2+\sqrt{3}$ $Q \geq\left(\frac{4 \sqrt{3}}{3}+1\right) \sqrt{3}-2=2+\sqrt{3}$ Dấu "=" xảy ra khi và chỉ khi

$a=b=c=\frac{1}{\sqrt{3}}$ $a=b=c=\frac{1}{\sqrt{3}}$. Suy ra $x=y=z=\sqrt{3}$ $x=y=z=\sqrt{3}$

Đề thi tuyển sinh lớp 10 môn Toán tỉnh Thanh Hóa năm 2020

Đáp án đề thi tuyển sinh lớp 10 môn Toán tỉnh Thanh Hóa năm 2020

Tham khảo thêm: Đáp án đề thi tuyển sinh lớp 10 môn Văn tỉnh Quảng Ninh năm 2020

.............................................

Ngoài Đáp án đề thi tuyển sinh lớp 10 môn Toán tỉnh Thanh Hóa năm 2020. Mời các bạn học sinh còn có thể tham khảo các đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề Thi vào lớp 10 năm 2024 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt

Chia sẻ, đánh giá bài viết

2

1.414

Bài trước

Bài sau

Chia sẻ bởi:
Đinh Thị Nhàn
Nhóm:
Sở GD&ĐT Thanh Hóa
Ngày: 04/08/2020

2 Bình luận

Sắp xếp theo

Xóa Đăng nhập để Gửi

Phùng Văn Thảo thầy nhầm câu viét
Thích Phản hồi 0 17/07/20
Lê Đức em đặt lộn đỉnh m và n nhưng vẫn cm // bình thường hỏi e bị trừ nhiều điểm k ạ
Thích Phản hồi 0 17/07/20