Đề thi tuyển sinh lớp 10 môn Toán chuyên năm 2020 THPT Chuyên Sư Phạm Hà Nội

Đề thi tuyển sinh vào lớp 10 môn Toán năm 2019 có đáp án

Đề thi tuyển sinh lớp 10 môn Toán Chuyên Sư Phạm Hà Nội năm 2020

Đề thi tuyển sinh lớp 10 môn Toán chuyên năm 2020 THPT Chuyên Sư Phạm Hà Nội do thư viện đề thi VnDoc.com sưu tầm. Đây là đề thi tham khảo vào lớp 10 môn Toán dành cho các bạn học sinh ôn tập, củng cố kiến thức, rèn luyện kĩ năng làm bài Toán. Mời các bạn cùng tham khảo

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 9, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 9 sau: Nhóm Tài liệu học tập lớp 9. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Đáp án đề thi tuyển sinh lớp 10 môn Toán chuyên THPT Chuyên Sư Phạm Hà Nội

Đề thi tuyển sinh lớp 10 môn Toán chuyên năm 2020 THPT Chuyên Sư Phạm Hà Nội

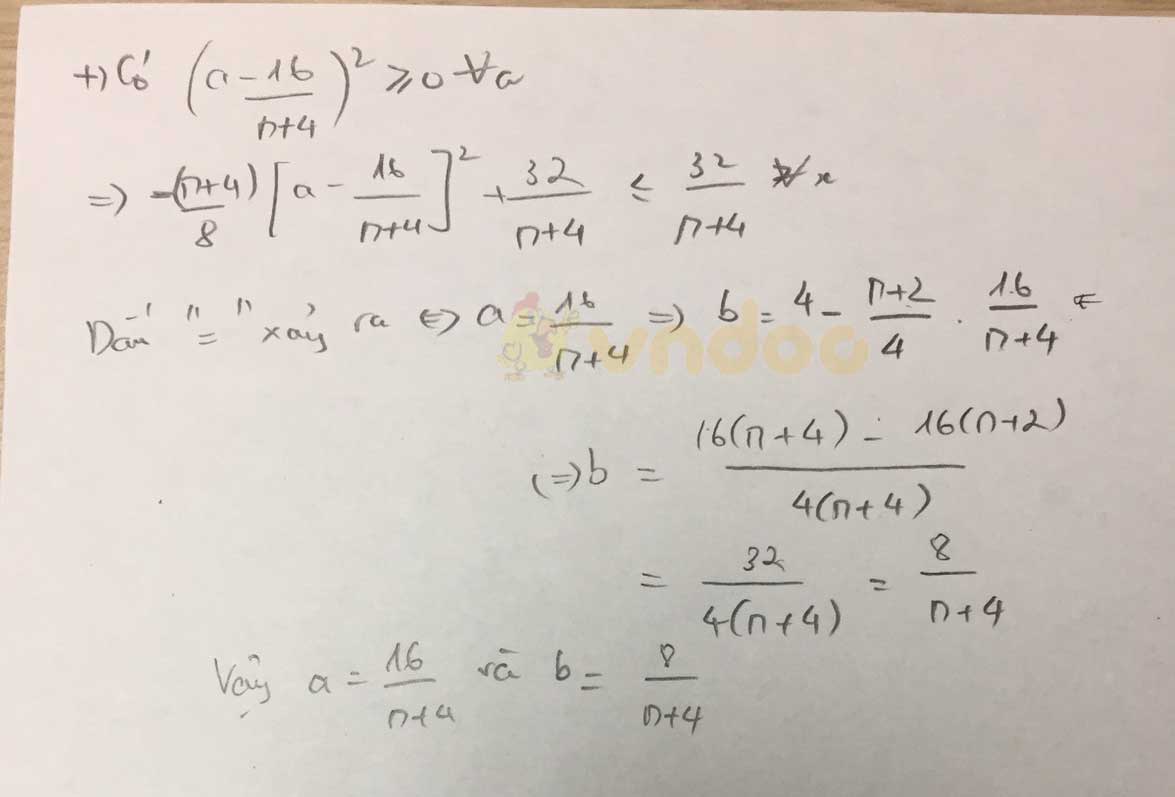
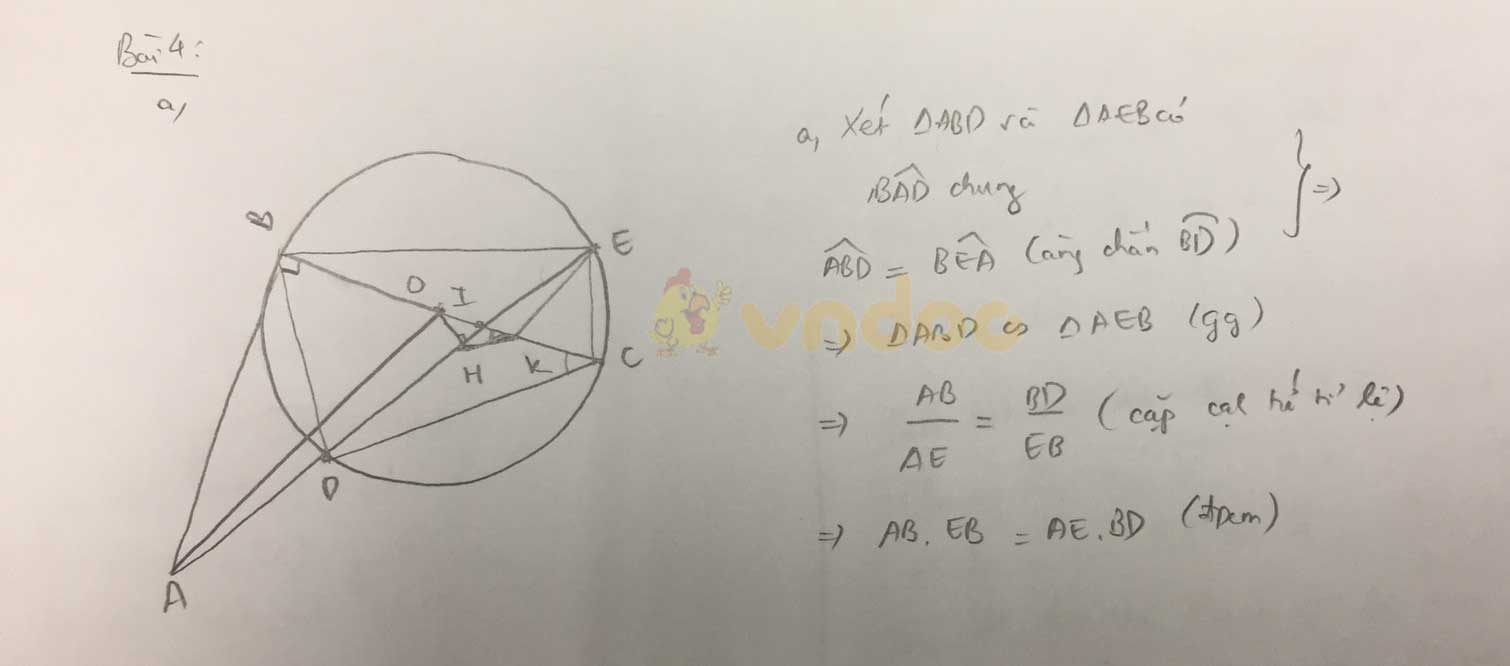
b.

Vì AB là tiếp tuyến của (O)=> OA⊥AB=> OBA = 90°. DE là dây cung của (O) mà H là trung điểm của DE

=> OH⊥ DE => ∠OHA = 90°.

Xét tứ giác ABOH có: ∠OHA + ∠OBA = 90° + 90° =180° nên tứ giác ABOH nội tiếp.

=> ∠HAO = ∠HBO (hai góc cùng chắn một cung (1)

Mà EK // AO => ∠KEA = ∠ HAO (hai góc sole trong) (2)

Từ (1) và (2) => ∠KEH = ∠KBH. => Tứ giác HKEB nội tiếp (dấu hiệu tứ giác nội tiếp)

=> ∠EHK = ∠KBE. (3)

Vì tứ giác DCEB nội tiếp => ∠CDE = ∠CBE (hai góc cùng chắn cung CE). (4)

Từ (3) và (4)=> ∠CDE = ∠KHE mà hai góc nằm ở vị trí đồng vị HK // DC.

c.

Xét tứ giác OTAB có OTA+ OBA =180° mà hai góc đối nhau

=> Tứ giác OTAB nội tiếp

=> ∠OAT = ∠OBT (góc nội tiếp cùng chắn cung OI).

Mà trên (O) có: ∠OBT = ∠CBT = ∠CDT (góc nội tiếp cùng chắn cung CT)

=> ∠OAT = ∠ CDT hay ∠PAT = ∠CDT => ∠PAT+ ∠PDT = 180°

Mà hai góc ở vị trí đối nhau trong tứ giác TAPD => TAPD là tứ giác nội tiếp.

=> ∠ATP = ∠ADP (góc nội tiếp cùng chắn cung AP).

Trên (O) có ∠EBC = ∠EDC (góc nội tiếp cùng chắn cung CE).

Mà ∠ADP = ∠EDC (hai góc đối đỉnh)

=> ∠ATP = ∠CBE (1)

AT; AB là tiếp tuyến của (O) => AO là phân giác của góc TAB => ∠TAP = ∠BAP

Xét △TAP và △BAP có:

AT = AB;
∠TAP = ∠BAP (cmt);
AP chung

=> △TAP và △BAP (c.g.c) (2).

Từ (1) và (2) ∠ABP = ∠EBC

-> EBP = ∠EBC + ∠CBP = ∠ABP+ ∠CBP = ∠CBA 90° => EBF = 90°

Mà EF qua 0, nên EF là đường kính của (O) suy BFCE có 2 đường chéo EF và BC bằng nhau và cắt nhau tại trung điểm mỗi đường nên nó là hình chữ nhật

Bài 5:

Ta có:

$1 \geq x,y,z > 0$ $1 \geq x,y,z > 0$

$⇒ 1 \geq x^2 và y \geq xy ⇒ 1 + y + zx \geq x^2 + xy + zx$ $⇒ 1 \geq x^2 và y \geq xy ⇒ 1 + y + zx \geq x^2 + xy + zx$

$\Leftrightarrow \dfrac{x}{1+y+zx} \leq \dfrac{x}{x^2+xy+zx} = \dfrac{1}{x+y+z}$ $\Leftrightarrow \dfrac{x}{1+y+zx} \leq \dfrac{x}{x^2+xy+zx} = \dfrac{1}{x+y+z}$

Chứng minh tương tự, ta có:

$\dfrac{y}{1+z+xy} \leq \dfrac{1}{x+y+z}$ $\dfrac{y}{1+z+xy} \leq \dfrac{1}{x+y+z}$

và $\dfrac{z}{1+x+yz} \leq \dfrac{1}{x+y+z}$ $\dfrac{z}{1+x+yz} \leq \dfrac{1}{x+y+z}$

Cộng vế theo vế, ta có:

$\dfrac{x}{1+y+zx}+ \dfrac{y}{1+z+xy}+ \dfrac{z}{1+x+yz} \leq \dfrac{3}{x+y+z} (*)$ $\dfrac{x}{1+y+zx}+ \dfrac{y}{1+z+xy}+ \dfrac{z}{1+x+yz} \leq \dfrac{3}{x+y+z} (*)$

Để hệ đã cho có nghiệm ⇔ Dấu bằng của BĐT (*) xảy ra hay x = y = z.

Thay vào ta có:

$\dfrac{3x}{1+x+x^2}= \dfrac{3}{3x}$ $\dfrac{3x}{1+x+x^2}= \dfrac{3}{3x}$

$\Leftrightarrow 3x^2= 1+x+x^2$ $\Leftrightarrow 3x^2= 1+x+x^2$

$\Leftrightarrow 2x^2-x-1=0$ $\Leftrightarrow 2x^2-x-1=0$

$\Leftrightarrow \left[ \matrix{ {x} = 1 &(tm) \hfill \cr {x} =-\dfrac{1}2 &(loại) \hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ {x} = 1 &(tm) \hfill \cr {x} =-\dfrac{1}2 &(loại) \hfill \cr} \right.$

⇒ x = y = z = 1.

Đề thi tuyển sinh lớp 10 môn Toán Chuyên Sư Phạm Hà Nội

Đề thi tuyển sinh lớp 10 môn Toán chuyên năm 2020 THPT Chuyên Sư Phạm Hà Nội

Trên đây VnDoc đã hướng dẫn các bạn giải Đề thi Toán chuyên Sư Phạm 2020. Hy vọng với đề thi này sẽ là tài liệu hữu ích cho các bạn tham khảo chuẩn bị cho kì thi vào lớp 10 THPT sắp tới.

.............................................

Ngoài Đề thi tuyển sinh lớp 10 môn Toán chuyên năm 2020 THPT Chuyên Sư Phạm Hà Nội. Mời các bạn học sinh còn có thể tham khảo các đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề Thi vào lớp 10 năm 2024 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt

Chia sẻ, đánh giá bài viết

1

521

Bài trước

Bài sau