VnDoc.com

Đề khảo sát Toán (chuyên) vào lớp 10 trường THPT chuyên Thái Nguyên năm 2025 - 2026

Ôn thi vào lớp 10 môn Toán có đáp án

Tải về

Lớp: Ôn vào 10

Môn: Toán

Dạng tài liệu: Đề thi

Loại File: PDF

Phân loại: Tài liệu Tính phí

SỞ GIÁO DỤC VÀ ĐÀO TẠO THÁI NGUYÊN

TRƯỜNG THPT CHUYÊN

ĐỀ THI KHẢO SÁT VÀO LỚP 10 MÔN TOÁN

NĂM HỌC 2025 – 2026

(Dành cho thí sinh thi vào chuyên Toán)

Th

ờ

i gian làm bài:

150

phút

.

(ĐỀ THI GỒM CÓ 01 TRANG)

Câu 1 (1,5 điểm). Cho biểu thức

1 3

: 2

1 3 2 3 1

x x x

S

x x x x x

 



 

   

 

    

 

a) Tìm điều kiện xác định và rút gọn biểu thức

.

S

b) Tìm tất cả các số thực

x

thoả mãn





3 1. 2 5 2 .

x x S x x

    

Câu 2 (1,5 điểm).

a) Giải hệ phương trình

2 2

3 3

2

.

4

3

x y



 





 







b) Từ một tấm bìa hình tam giác vuông cân có cạnh bên bằng 10 dm, bác An cắt một hình

chữ nhật có hai đỉnh thuộc cạnh đáy và mỗi cạnh bên chứa một đỉnh còn lại để làm biển

quảng cáo. Hỏi bác An có thể cắt được hình chữ nhật có diện tích lớn nhất là bao nhiêu?

Câu 3 (1,0 điểm). Bạn Ân thực hiện một thí nghiệm: Gieo một con xúc sắc có sáu mặt cân

đối, đồng chất hai lần liên tiếp.

a) Tính số phần tử của không gian mẫu



.

b) Tính xác suất của biến cố A: “Tổng hai lần gieo là một số nguyên tố”.

Câu 4 (1,0 điểm). Tìm tất cả các số nguyên

n

để biểu thức

4 3 2

2 4 2 3

A n n n n

    

là

số chính phương.

Câu 5 (1,0 điểm). Cho

p

là số nguyên tố lớn hơn 5 và

2

4 1

3

p

n





. Chứng minh rằng

5

4 1

n



chia hết cho

3 .

n

Câu 6 (1,0 điểm). Cho tập hợp





1; 2;...; 4048 .

S



Chứng minh rằng khi chọn 2025 số bất

kì trong tập

S

ta luôn chọn được 2 số trong 2025 số đó mà số này là bội của số kia.

Câu 7 (3,0 điểm). Cho tam giác

ABC

cân tại

A

ngoại tiếp đường tròn





.

I

Một tiếp tuyến

bất kì của đường tròn





I

tại điểm

P

cắt hai đoạn thẳng

,

AB AC

lần lượt tại

,

F E

(

E

khác

A

và

,

C

F

khác

A

và

B

). Hạ

,

EK FL

cùng vuông góc với





, .

BC K L BC



Gọi

FK

cắt

LE

tại điểm

.

J

Hạ

JH

vuông góc với





.

BC H BC



a) Chứng minh rằng



.

EHJ FHJ



b) Chứng minh rằng

2 2

. . .

CEJK BFJL

BF S CE S

c) Gọi

M

là giao điểm của

PJ

và

.

EK

Chứng minh rằng

.

MK PF CE

ME PE BF



------------------------------- HẾT----------------------------------

Họ tên thí sinh ………………………………………..Số báo danh ……………….

HƯỚNG DẪN CHẤM THI KHẢO SÁT VÀO LỚP 10 MÔN TOÁN

NĂM HỌC 2025 – 2026

(Dành cho thí sinh thi vào chuyên Toán)

Câu Nội dung Điểm

Câu 1

Cho biểu thức

1 3

: 2

1 3 2 3 1

x x x

S

x x x x x

 



 

   

 

    

 

a) Tìm điều kiện xác định và rút gọn biểu thức

.

S

b) Tìm tất cả các số thực

x

thoả mãn





3 1. 2 5 2

x x S x x

    

1,5 đ

a) ĐKXĐ

0

1

x













 







Ta có:

    

  

 

  

1 3

: 2

1 3 2 3 1

3 1 1 2 1 3

:

1

1 3

3 1 2 1

:

1

1 3

2 1 1 1

.

2 1 3

1 3

x x x

S

x x x x x

x x x x x x

S

x

x x

x x x x x

S

x

x x

S

x x

 



 

   

 

    

 

      





 

    





 

 

 

 

 

0.25

0,25

b) Ta có





   

 

1

3 1. 2 5 2

3

1 1 2 5 3 2 4 0 1

2 2

2

2 2 0

1 1 2 5 3

1 2

2 2 0

1 1 2 5 3

x x x x

x

x x x x

x

x x

x

x x

    



        



   

   

 

   

 

   

 

Nhận xét

1 2 2

2 1 2 0

3

1 1 2 5 3x x

     

   

suy ra





2 TM

x



0,25

Câu 2

a) Giải hệ phương trình

2 2

3 3

2

.

4

3

x y



 





 







b) Từ một tấm bìa hình tam giác vuông cân có cạnh bên bằng 10 dm, bác

An cắt một hình chữ nhật có hai đỉnh thuộc cạnh đáy và mỗi cạnh bên chứa

một đỉnh còn lại để làm biển quảng cáo. Hỏi bác An có thể cắt được hình

chữ nhật có diện tích lớn nhất là bao nhiêu?

1,5 đ

a) Ta có





 

2

2 2

3 3

4 3 3 4 4 4 2 2

4 3 2 2 3 4

3

3 3 2 0

2 3 2 2 0 *

x y

x y x y

x y

x xy x y y x y x y

x x y x y xy y



   



      

    

Nhận xét: Nếu

0

y



suy ra

0

x



(Vô lý)

Vậy

0

y



. Chia cả hai vế phương trình (*) cho

4

y

và đặt

 

1

x

t t

y

  

ta

được phương trình:

4 3 2

2 3 2 2 0

t t t t

    

suy ra

1

t



hoặc

2

t

 

(TM)

Với

1

t



suy ra

x y



. Ta có

2

2 2

x



suy ra

1

x y

  

Với

2

t

 

suy ra

2

x y

 

. Ta có

2

5 2

y



suy ra

10 2 10

;

5 5

y x



 

hoặc

10 2 10

;

5 5

y x



 

Vậy hệ phương trình có 4 nghiệm

   

2 10 10 2 10 10

1;1 , 1; 1 , ; , ;

5 5 5 5

   

 

   

   

0,25

b)

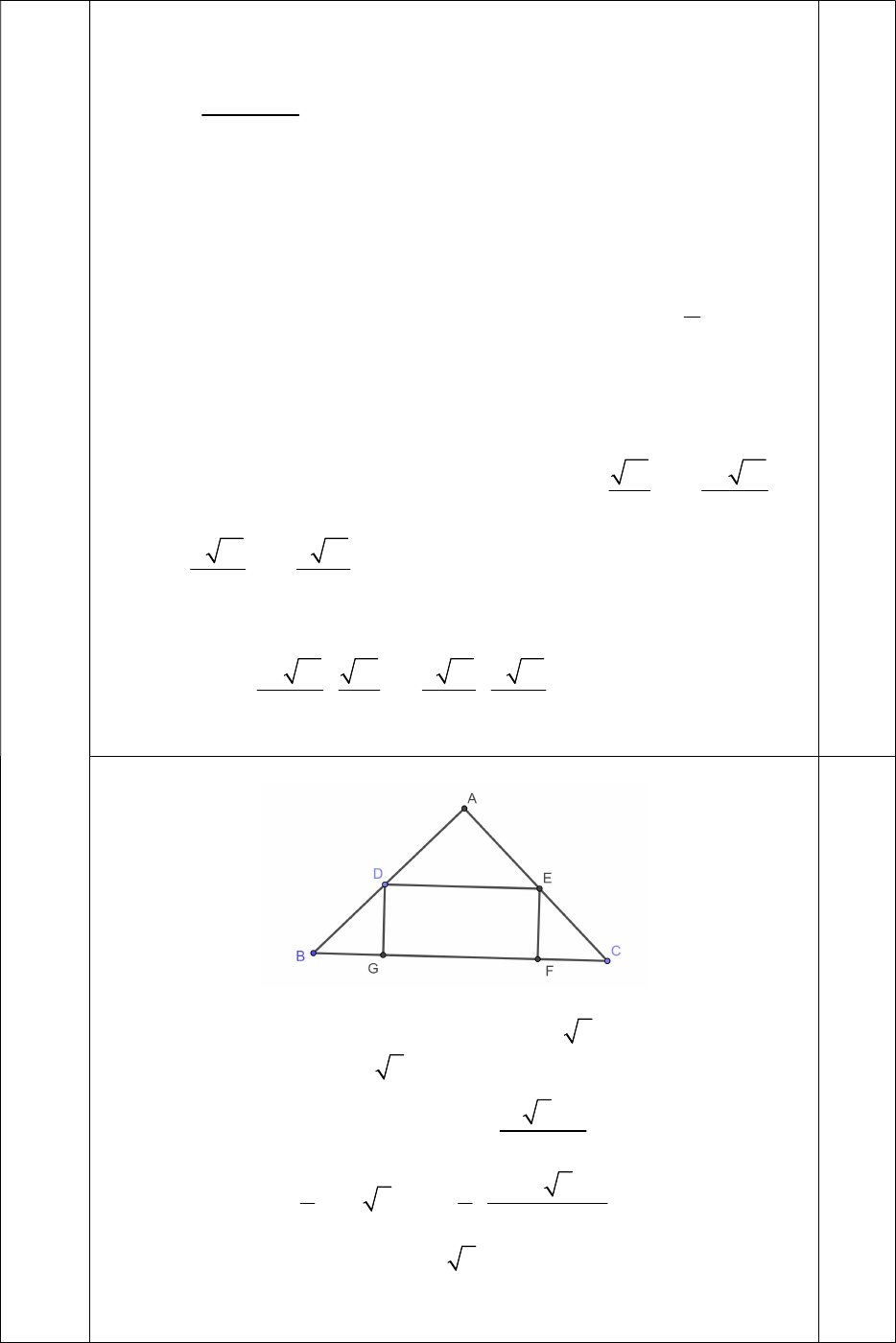
Xét tam giác vuông cân ABC có cạnh bên AB = AC = 10 dm. Bác An cắt

hình chữ nhật DEFG như hình vẽ. Ta có

10 2

BC 

Đặt





0 10 2

DE FG x x    . Khi đó ta có

,

BGD CFE

 

vuông cân

tại G và F. Suy ra

10 2

2

x

BG GD EF FC



   

.

Khi đó ta có

 

2

1 1 10 2

10 2 25

2 2 2

DEFG

x x

S x x

 

 

   

 

 

Suy ra

2

max 25

DEFG

S dm

 khi

5 2.

x 

Vậy diện tích của tấm bìa hình chữ nhật mà bác An có thể cắt lớn nhất là

2

25 .

dm

0,25

Đề minh họa thi vào 10 môn Toán 2025

VnDoc giới thiệu đến quý thầy, cô giáo và các em học sinh Đề khảo sát Toán (chuyên) vào lớp 10 trường THPT chuyên Thái Nguyên năm 2025 - 2026. Tài liệu với cấu trúc trắc nghiệm và tự luận, có đáp án và hướng dẫn giải cho các em so sánh và đối chiếu với bài làm của mình.

Ngoài tài liệu trên, VnDoc còn gửi tới các bạn nhiều tài liệu tuyển sinh vào lớp 10 các môn để giúp các em ôn luyện, làm quen với nhiều đề thi khác nhau, chuẩn bị cho kì thi tuyển sinh vào lớp 10 năm học 2025 - 2026.

Tải về

Chọn file muốn tải về: