Đề khảo sát Toán (chuyên) thi vào 10 trường chuyên Lam Sơn, Thanh Hóa năm 2025 - 2026
Ôn thi vào lớp 10 môn Toán có đáp án
Lớp:
Ôn vào 10
Môn:
Toán
Dạng tài liệu:
Đề thi
Loại:
Tài liệu Lẻ
Loại File:
PDF
Phân loại:
Tài liệu Tính phí
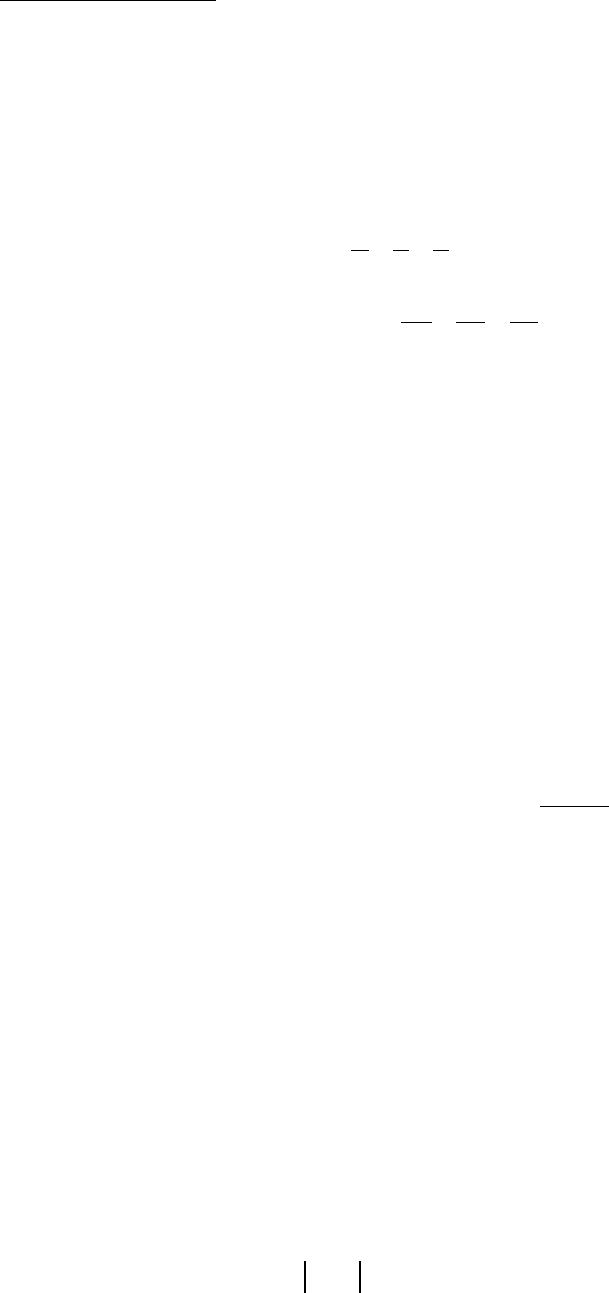
SỞ GD & ĐT THANH HÓA
TRƯỜNG THPT CHUYÊN LAM SƠN
ĐỀ THI CHÍNH THỨC
(Đề thi có 01 trang)
KỲ THI KHẢO SÁT CÁC MÔN THI VÀO LỚP 10
THPT CHUYÊN LAM SƠN
Năm học: 2025 – 2026
Môn thi: TOÁN
(Dành cho thí sinh thi vào chuyên Toán)
Ngày thi: 06/4/2025
Thời gian làm bài:150 phút (không kể thời gian phát đề)
Câu 1. (2,0 điểm).
a) Cho ba số
,,abc
khác
0
thỏa mãn
111
0
abc
++=
, tính giá trị biểu thức
2 22
ab bc ca
A
cab
=++
.
b) Cho đa thức
( )
Px
với hệ số nguyên, chứng minh rằng không tồn tại ba số nguyên phân biệt
,,
abc
sao cho
(
) ( ) ( )
,,PabPbcPca= = =
.
Câu 2 (1,0 điểm).
Xét hệ phương trình:
2
2
()
()
y xy m
x xy m
−+=
−+=
(với
m
là tham số), tìm
m
để hệ có nghiệm duy nhất.
Câu 3 (1,0 điểm).
Có
10
bạn (trong đó chỉ có một bạn tên An và một bạn tên Bảo) xếp ngẫu nhiên thành một hàng
dọc, tính xác suất để trong đó nhất thiết có 2 bạn An và Bảo phải đứng cạnh nhau.
Câu 4 (2,0 điểm)
a) Chứng minh rằng tồn tại vô số số nguyên dương n thỏa mãn tính chất
( )
21
n
n+
.
b) Cho
p
là số nguyên tố, chứng minh phương trình
2
4
2
xx
p
yy
+
=
+
không có nghiệm nguyên
dương.
Câu 5 (3,0 điểm).
Cho tam giác
ABC
nhọn (
AB AC<
) nội tiếp đường tròn
()O
, ngoại tiếp đường tròn
()I
. Đường
thẳng đi qua
I
vuông góc với
AI
cắt
BC
tại
T
.
a) Chứng minh
TI
là tiếp tuyến của đường tròn ngoại tiếp tam giác
BIC
.
b)
AI
cắt lại
()O
tại
D
(
D
khác
A
), đoạn
TI
cắt
()O
tại
Q
,
QD
cắt
BC
tại
P
. Chứng minh
rằng
2
..
IP PB PC=
c) Gọi
,EF
là tiếp điểm của
()I
theo thứ tự với
,AC AB
và
N
là trung điểm
EF
. Chứng minh
rằng
BNC
tù.
Câu 6 (1,0 điểm).
Trên bảng có viết
2025
số nguyên dương từ
1
đến
2025
. Mỗi lần ta được phép xóa đi 2 số
,
ab
tùy ý có trên bảng và thay bởi số
ab−
. Thực hiện cho tới khi trên bảng chỉ còn đúng một số là
m
. Tìm giá trị nhỏ nhất có thể có của
m
.
………………………….. Hết …………………………
Cán bộ coi thi không giải thích gì thêm
Họ và tên thí sinh: ................................................................... Số báo danh: ..........................
Chữ kí của giám thị số 1: ……………………………………..….Chữ kí của giám thị số 2:………………

SỞ GD & ĐT THANH HÓA
TRƯỜNG THPT CHUYÊN LAM SƠN
HƯỚNG DẪN CHẤM
KỲ THI KHẢO SÁT CÁC MÔN THI VÀO LỚP 10
THPT CHUYÊN LAM SƠN
Năm học: 2025 – 2026
Môn thi: TOÁN
(Dành cho thí sinh thi vào chuyên Toán)
Ngày thi: 06/4/2025
Thời gian làm bài:150 phút (không kể thời gian phát đề)
Câu 1 (2,0 điểm).
a) Cho ba số
,,abc
khác
0
thỏa mãn
111
0
abc
++=
, tính giá trị biểu thức
2 22
ab bc ca
A
cab
=++
.
b) Cho đa thức
( )
Px
với hệ số nguyên, chứng minh rằng không tồn tại ba số nguyên phân biệt
,,
abc
sao cho
(
) ( ) ( )
,,PabPbcPca= = =
.
Giải
a) Từ đẳng thức
3 33 2 22
3 ( )( ),x y z xyz x y z x y z xy yz zx+ + − = ++ + + − + +
với
0xyz++=
thì
3 33
3
x y z xyz
++=
.
Vì
111
0
abc
++=
nên
333
111 3
abc
abc
++=
2 22
3
ab bc ca
A
cab
⇒= + + =
, vậy
3A =
.
b) Giả sử tồn tại ba số nguyên phân biệt
,,abc
sao cho
( ) ( ) ( )
,,PabPbcPca= = =
, không mất
tính tổng quát nếu giả sử b là số lớn nhất (b > a, b > c). Khi đó ta có
(
)
( ) (
)
(
) ( )
( )
( ) ( ) ( )
Pa Pb a b
Pb Pc b c
Pc Pa c a
− −
−−
−−
( ) ( )
( ) ( )
( ) ( )
0
0
0
bc ab
ca bc
ab ca
≠ − −
⇒ ≠− −
≠− −
bc ab
ca bc
ab ca
−≥−
⇒ −≥−
−≥−
ab ca bc ab⇒−≥−≥−≥−
ab ca bc
⇒−=−=−
ab bc⇒−=−
ba bc a c⇒−=−⇒ =
vô lý.
Vậy không tồn tại ba số nguyên phân biệt
,,abc
thỏa mãn đề bài.
Câu 2 (1,0 điểm).
Cho hệ phương trình:
2
2
()
()
y xy m
x xy m
−+=
−+=
(với
m
là tham số), tìm
m
để hệ có nghiệm duy nhất.
Giải
Nhận xét nếu
( )
00
,
xy
là một nghiệm của hệ thì
( )
00
,yx
cũng là một nghiệm của hệ. Nếu hệ có
nghiệm duy nhất thì
00
xy=
, từ hệ suy ra phương trình:
2
20x xm− −=
.
Do hệ có nghiệm duy nhất nên phương trình trên phải có nghiệm duy nhất.
'
10m⇒∆ = + =
1m⇒=−
.
Với
1m = −
ta có hệ:
2
2
( )1
( )1
y xy
x xy
−+=−
−+=−
( ) ( )
22
1 10xy⇒− +− =
1xy⇔==
thỏa mãn bài toán.
Vậy đáp số bài toán
1m = −
.
Câu 3 (1,0 điểm).

Có 10 bạn (trong đó chỉ có một bạn tên An và một bạn tên Bảo) xếp ngẫu nhiên thành một hàng
dọc, tính xác suất để trong đó nhất thiết có 2 bạn An và Bảo phải đứng cạnh nhau.
Giải
Số cách xếp 10 bạn xếp thành một hàng dọc là
10!
Xem An và Bảo là “1 bạn” thì số cách xếp 9 “bạn” thành 1 hàng dọc là 9!, đổi chỗ An và Bảo
cho nhau được cách xếp 10 bạn mà trong đó An và Bảo đứng cạnh nhau là 2.9!.
Vậy xác suất để trong đó nhất thiết có 2 bạn An và Bảo phải đứng cạnh nhau là:
2.9! 1
10! 5
=
.
Câu 4 (2,0 điểm)
a) Chứng minh rằng tồn tại vô số số nguyên dương n thỏa mãn tính chất
( )
21
n
n+
b) Cho
p
là số nguyên tố, chứng minh phương trình
2
4
2
xx
p
yy
+
=
+
không có nghiệm nguyên
dương.
Giải
a) Ta có nhận xét sau: nếu
( )
21
n
n+
thì
( )
21
m
m+
với
21
n
m = +
Thật vậy do
( )
21
n
n+
và
( )
21
n
+
lẻ nên
n
lẻ, đặt
21
n
m nl= +=
( l là số lẻ)
Ta có:
( ) ( ) ( ) ( ) ( )
12
2 1 2 1 2 1 2 2 ... 2 1
l ll
m n nnn n
−−
+= += + − + − +
suy ra
(
) (
)
2 12 1
mn
++
hay
( )
21
m
m+
(nhận xét đã được chứng minh)
Với n = 1, n = 3 thỏa mãn tính chất, cho nên,
39
2 1 9, 2 1...nn= += = +
cũng thõa mãn. Đậy là
điều phải chứng minh.
b) Phương trình đã cho tương đương với:
( ) ( )
4
11xx yy p
+= +
(1) suy ra
( )
4
1xx p+
, mặt khác
ta có
(
)
, 11xx+=
nên
4
xp
hoặc
( )
4
1xp+
.
*) Xét
4
xp
, đặt
(
)
4*
x pk k
= ∈
thay vào phương trình ta được:
(
)
( )
44 4
11pk pk py y+= +
⇔
(
)
( )
4
11k pk y y
+= +
⇔
( )
( )
22
kp y kp y y k− +=−
Nếu y = k suy ra p = 1 vô lý.
Nếu
yk
>
suy ra
( )
22
10y k kp y k p−≥ +⇒ + ≤
vô lý
Nếu
yk
<
suy ra
2
y pk<
( )
( )
22
0kp y kp y y k⇒ − + >>−
vô lý.
*) Nếu
( )
4
1xp+
xét tương tự ta cũng suy ra vô lý.
Vậy phương trình đã cho không có nghiệm nguyên dương.
Câu 5 (3,0 điểm).
Cho tam giác
ABC
nhọn (
AB AC<
) nội tiếp đường tròn
()O
, ngoại tiếp đường tròn
()I
. Đường
thẳng đi qua
I
vuông góc với
AI
cắt
BC
tại
T
.
a) Chứng minh
TI
là tiếp tuyến của đường tròn ngoại tiếp tam giác
BIC
.
b)
AI
cắt lại
()O
tại
D
(
D
khác
A
), đoạn
TI
cắt
()O
tại
Q
,
QD
cắt
BC
tại
P
. Chứng minh
rằng
2
..IP PB PC=
c) Gọi
,EF
là tiếp điểm của
()I
theo thứ tự với
,AC AB
và
N
là trung điểm
EF
. Chứng minh
rằng
BNC
tù.
Giải
Đề minh họa thi vào 10 môn Toán 2025
VnDoc giới thiệu đến quý thầy, cô giáo và các em học sinh Đề khảo sát Toán (chuyên) thi vào 10 trường chuyên Lam Sơn, Thanh Hóa năm 2025 - 2026. Tài liệu với cấu trúc trắc nghiệm và tự luận, có đáp án và hướng dẫn giải cho các em so sánh và đối chiếu với bài làm của mình.
Ngoài tài liệu trên, VnDoc còn gửi tới các bạn nhiều tài liệu tuyển sinh vào lớp 10 các môn để giúp các em ôn luyện, làm quen với nhiều đề thi khác nhau, chuẩn bị cho kì thi tuyển sinh vào lớp 10 năm học 2025 - 2026.




