Đề thi thử tuyển sinh lớp 10 môn Toán sở GD&ĐT Bắc Giang năm 2025 - 2026
Ôn thi vào lớp 10 môn Toán có đáp án
Lớp:
Ôn vào 10
Môn:
Toán
Dạng tài liệu:
Đề thi
Loại:
Tài liệu Lẻ
Loại File:
PDF
Phân loại:
Tài liệu Tính phí
Trang 1/3 - Mã đề thi 911
SỞ GIÁO DỤC VÀ ĐÀO TẠO
BẮC GIANG
ĐỀ THI THỬ
(Đề thi gồm 03 trang)
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT
NĂM HỌC 2025 - 2026
MÔN: TOÁN
Thời gian làm bài: 120 phút, không kể thời gian giao đề.
Mã đề thi: 911
I. PHẦN TRẮC NGHIỆM (3,0 điểm).
Câu 1. Một công ty sản xuất và đưa ra bán trên thị trường sản phẩm
A
. Theo tính toán, khi đơn giá của
mỗi sản phẩm
A
là
x
nghìn đồng thì doanh thu
P
(đơn vị nghìn đồng) là
( )
2
560 50000Px x x
=−+
.
Doanh thu tháng đầu tiên của công ty khi bán sản phẩm
A
với giá ưu đãi là 996 triệu đồng. Biết giá bán
ưu đãi của sản phẩm
A
không vượt quá 50 nghìn đồng, hỏi giá ưu đãi của sản phẩm
A
mà công ty đã
bán ở tháng đầu tiên là bao nhiêu?
A.
32000
đồng. B.
30000
đồng. C.
300000
đồng. D.
35000
đồng.
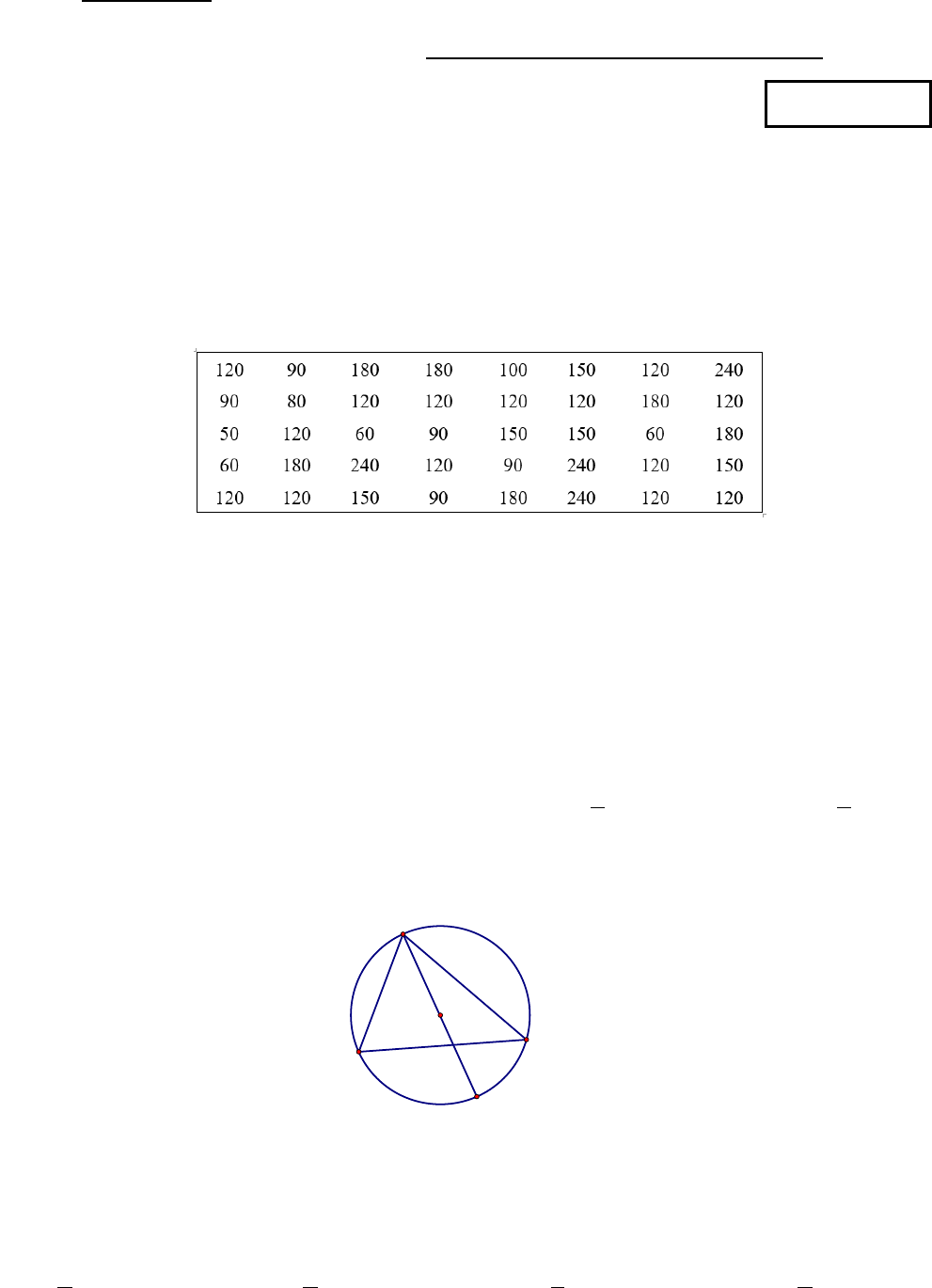
Câu 2. Thời gian tự học (tính theo phút) trong một ngày của 40 học sinh lớp 9A được ghi lại trong bảng sau:
Tần số tương đối của học sinh có thời gian tự học 120 phút một ngày là
A.
25%.
B.
20%.
C.
35%.
D.
50%.
Câu 3. Cho hai đường tròn:
( )
;4cmO
và
( ;5 cm)I
. Nếu
1cm
OI =
thì hai đường tròn đã cho
A. tiếp xúc trong. B. không giao nhau. C. cắt nhau. D. tiếp xúc ngoài.
Câu 4. Cặp số
( )
,xy
nào sau đây là nghiệm của hệ phương trình
32 5
23 1
xy
xy
−=
+=−
?
A.
( )
1; 1 .−−
B.
( )
1;1 .−
C.
( )
1; 1 .−
D.
(
)
1;1 .
Câu 5. Phương trình
( )
2
2 1 4 10m x xm− + + −=
là phương trình bậc hai khi
A.
1.m ≠
B.
0.m ≠
C.
1
.
2
m
≠
D.
1
.
2
m =
Câu 6. Cho tam giác
ABC
nội tiếp đường tròn
( )
O
đường kính
AD
(như hình vẽ). Biết
o
25DAC =
. Số
đo
ABC
bằng
O
B
C
A
D
A.
o
130 .
B.
o
90 .
C.
o
65 .
D.
o
50 .
Câu 7. Một chiếc hộp chứa ba quả bóng có kích thước và khối lượng như nhau chỉ khác màu, trong đó có
1 quả bóng màu xanh, 1 quả bóng màu vàng và 1 quả bóng màu hồng. Lần lượt lấy ra ngẫu nhiên từng
quả bóng từ trong hộp cho đến khi hộp hết bóng. Xác suất của biến cố ‘‘Quả bóng cuối cùng lấy ra có
màu xanh’’ là
A.
1
.
6
B.
2
.
3
C.
1
.
3
D.
1
.
2
Câu 8. Biết
8−
là một căn bậc hai của
x
. Căn bậc ba của
x
bằng
A.
2.−
B.
4.
C.
64.
D.
2.

Trang 2/3 - Mã đề thi 911
Câu 9. Lớp 9A có
38
học sinh tham gia buổi lao động trồng cây gây rừng. Biết cả lớp trồng được tất cả
170 cây xanh, trong đó mỗi bạn nữ trồng 4 cây, mỗi bạn nam trồng 5 cây. Nếu gọi số học sinh nam là
x
và số học sinh nữ là
y
thì
, xy
thoả mãn hệ phương trình nào sau đây?
A.
38
.
5 4 170
xy
xy
+=
−=
B.
38
.
5 4 170
xy
xy
+=
+=
C.
38
.
4 5 170
xy
xy
+=
+=
D.
38
.
4 5 170
xy
yx
+=
−=
Câu 10. Để trang trí lớp, bạn Lan đã dùng 4 miếng bìa hình quạt tròn cung
o
120
, bán kính 30 cm (hình
vẽ) để gấp trang trí. Tổng diện tích các miếng bìa bạn Lan đã dùng là
A.
2
300 cm
π
. B.
2
1200 cm
π
. C.
2
1500 cm
π
. D.
2
2400 cm
π
.
Câu 11. Với
0, 0
ab
><
thì biểu thức
3
2
ba
A
ab
−
=
bằng
A.
.a
B.
.
a
a
b
C.
.a−
D.
.
a
a
b
−
Câu 12. Tất cả các giá trị của biến
x
để biểu thức
42x
−
có nghĩa là
A.
0.x ≥
B.
2.x ≥−
C.
1
.
2
x
−
≥
D.
1
.
2
x
≥
Câu 13. Nam muốn mua một chiếc xe đạp có giá 3200000 đồng. Hiện tại, Nam đã có 1200000 đồng. Nam
dự định mỗi tháng sẽ tiết kiệm một số tiền cố định như nhau từ tiền ăn sáng và tiền tiêu vặt mà bố mẹ cho
để mua xe. Hỏi Nam cần tiết kiệm ít nhất bao nhiêu tiền mỗi tháng để sau 8 tháng có đủ tiền mua xe?
A.
200000
đồng. B.
250000
đồng. C.
300000
đồng. D.
25000
đồng.
Câu 14. Tính độ dài đường tròn ngoại tiếp tam giác
ABC
vuông tại
A
có
6 cm, 8 cmAB AC= =
.
A.
40 cm.
π
B.
5 cm.
π
C.
10 cm.
π
D.
20 cm.
π
Câu 15. Hàm số
( ) ( )
2
11y m xm=−≠
có đồ thị nằm phía trên trục hoành khi
A.
1.m >
B.
1.m >−
C.
1.m <−
D.
1.m <
Câu 16. Chọn ngẫu nhiên một số có hai chữ số. Xác suất để số được chọn là số chính phương (là số bằng
bình phương đúng của một số nguyên) bằng bao nhiêu?
A.
2
45
. B.
1
15
. C.
7
90
. D.
1
10
.
Câu 17. Cho tam giác
MNP
vuông tại
M
. Trong các khẳng định sau khẳng định nào đúng?
A.
( )
sin cos 90 .
o
NP= −
B.
tan cot .MP
=
C.
tan .cot 1.NP=
D.
sin cos .NP=
Câu 18. Nếu đặt một chiếc thang dài 4 m cách chân tường 2 m (hình vẽ) thì góc tạo bởi thang và mặt đất bằng
A.
o
30 .
B.
o
60 .
C.
o
90 .
D.
o
50 .

Trang 3/3 - Mã đề thi 911
Câu 19. Biết hệ phương trình
2
3
x my
nx y
−=
+=
có nghiệm
( ) ( )
, 2;1xy =
. Khi đó giá trị của biểu thức
2025
2025mn+
bằng
A.
2025.
B.
1.
C.
2026.
D.
0.
Câu 20. Gieo ngẫu nhiên hai con xúc xắc cân đối đồng chất. Xác suất của biến cố A: “Tổng số chấm xuất
hiện trên hai con xúc xắc bằng 8” là
A.
5
.
36
B.
1
.
6
C.
1
.
9
D.
1
.
12
II. PHẦN TỰ LUẬN (7,0 điểm).
Câu 1: (2,5 điểm)
1) Tìm tham số
m
để đồ thị của hàm số
(
) (
)
2
11y mx m
=−≠
đi qua điểm
( )
2; 4M −−
.
2) Rút gọn biểu thức
2 131 4
:
1
11 1
x
P
x
xx x
−
= −+
−
+− +
với
0x ≥
và
1x ≠
.
3) Giải bất phương trình:
63 0
x−>
.
Câu 2: (1,0 điểm) Cho phương trình:
( )
2
2 30x m xm+ − − −=
(1) (
x
là ẩn,
m
là tham số).
1) Giải phương trình
( )
1
với
3
m
=
.
2) Tìm tất cả các giá trị của
m
để phương trình
(
)
1
có hai nghiệm
12
,xx
thoả mãn:
(
)
( )
2
11 2
2 3 5.x mx m x+ − +=
Câu 3: (1,0 điểm) AQI (Air Quality Index) là một chỉ số báo cáo chất lượng không khí hàng ngày. Đây
được coi là một thước đo đơn giản hóa mức độ ô nhiễm không khí, cho biết không khí xung quanh ta là
sạch hay ô nhiễm, ô nhiễm đến mức độ nào từ đó đánh giá được chất lượng không khí. Tiến hành đo chỉ
số chất lượng không khí (AQI) để đánh giá chất lượng không khí ở thành phố A tại cùng một thời điểm
trong 40 ngày, kết quả được ghi lại trong bảng sau:
Chất lượng không khí
Tốt
Trung bình
Kém
Xấu
Rất xấu
Nguy hại
Số ngày
6
16
12
4
2
0
1) Lập bảng tần số tương đối chất lượng không khí tại thành phố A trong 40 ngày đó.
2) Chọn ngẫu nhiên một ngày trong 40 ngày trên để xem chất lượng không khí của ngày được chọn đó.
Tính xác suất của biến cố: “Ngày được chọn ra có chất lượng không khí trung bình hoặc tốt”.
Câu 4: (2,0 điểm) Cho tam giác
ABC
( )
AB AC<
có ba góc nhọn nội tiếp đường tròn
(
)
O
. Các đường
cao
BM
và
CN
của tam giác
ABC
cắt nhau tại
H
( )
,M AC N AB∈∈
.
1) Chứng minh tứ giác
BNMC
là tứ giác nội tiếp.
2) Đường thẳng
,BM CN
cắt đường tròn
( )
O
lần lượt tại
( )
,,
PQ P BQ C≠≠
. Chứng minh:
..HM NQ HN MP
=
.
3) Gọi
I
là trung điểm của
BC
. Chứng minh:
2AH OI=
.
Câu 5: (0,5 điểm). Cho
,ab
là hai số thực dương thỏa mãn
1
ab ≥
. Tìm giá trị nhỏ nhất của biểu thức:
2
11 1
a b ab
P
b a ab
+
=++
++ +
.
------ HẾT ------
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh: .................................................................Số báo danh: ......................................
Cán bộ coi thi số 1 (Họ tên và chữ ký)...............................................................................................
Cán bộ coi thi số 2 (Họ tên và chữ ký)...............................................................................................
Đề minh họa thi vào 10 môn Toán 2025
VnDoc giới thiệu đến quý thầy, cô giáo và các em học sinh Đề thi thử tuyển sinh lớp 10 môn Toán sở GD&ĐT Bắc Giang năm 2025 - 2026. Tài liệu với cấu trúc trắc nghiệm và tự luận, có đáp án và hướng dẫn giải cho các em so sánh và đối chiếu với bài làm của mình.
Ngoài tài liệu trên, VnDoc còn gửi tới các bạn nhiều tài liệu tuyển sinh vào lớp 10 các môn để giúp các em ôn luyện, làm quen với nhiều đề thi khác nhau, chuẩn bị cho kì thi tuyển sinh vào lớp 10 năm học 2025 - 2026.




