Đề khảo sát Toán thi vào 10 lần 2 năm 2025 - 2026 trường chuyên Sơn Tây, Hà Nội
Ôn thi vào lớp 10 môn Toán có đáp án
Lớp:
Ôn vào 10
Môn:
Toán
Dạng tài liệu:
Đề thi
Loại:
Tài liệu Lẻ
Loại File:
PDF
Phân loại:
Tài liệu Tính phí
1
TRƯỜNG THPT CHUYÊN SƠN TÂY
CÔNG TY CỔ PHẦN GIÁO DỤC FAMILY
ĐỀ KHẢO SÁT KIẾN THỨC KỲ THI TUYỂN SINH
LỚP 10 THPT (LẦN 2)
NĂM HỌC 2025 – 2026
(Đề thi có 02 trang)
Môn thi: TOÁN
Thời gian làm bài: 120 phút
Bài I. (1,5 điểm)
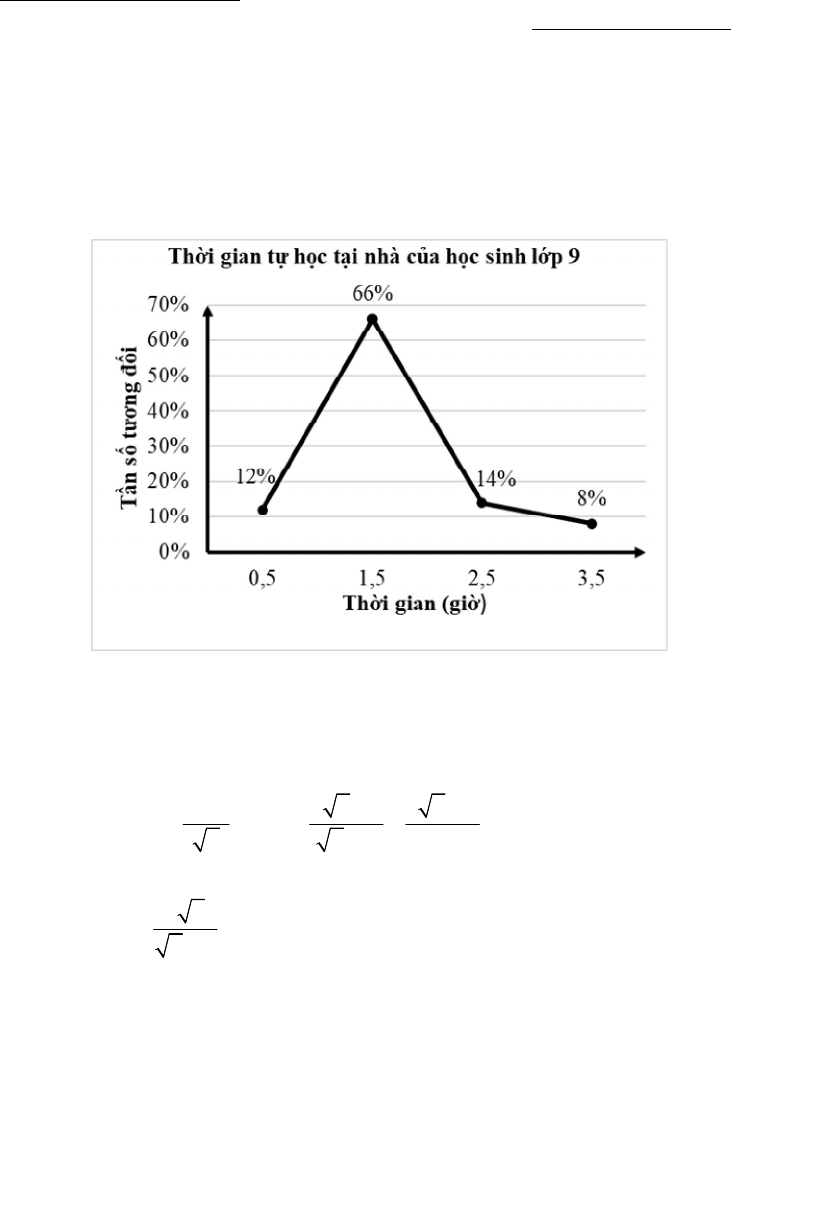
1) Thống kê thời gian tự học ở nhà của
350
học sinh lớp
9
tại một trường THCS ta được biểu đồ
đoạn thẳng biểu diễn tần số tương đối ghép nhóm với các nhóm
0;1
,
1;2
,
2;3
,
3;4
như sau:
Tìm tần số tương đối ghép nhóm và tần số ghép nhóm của nhóm có số học sinh tự học nhiều nhất.
2) Gieo một đồng xu cân đối đồng chất ba lần liên tiếp. Tính xác suất của biến cố
A
: “Có ít nhất
hai lần xuất hiện mặt ngửa”.
Bài II. (1,5 điểm)
Cho hai biểu thức:
2
x
A
x
và
2 3 5 6
4
2
x x
B
x
x
với
0, 4
x x
.
1) Tính giá trị của biểu thức
A
khi
16
x
.
2) Chứng minh
2
2
x
B
x
.
3) Tìm tất cả các giá trị nguyên của
x
để biểu thức
P AB
có giá trị nguyên.
Bài III. (2,5 điểm)
1) Trong kỳ thi tuyển sinh vào lớp
10
THPT năm 2024-2025, toàn thị xã Sơn Tây có
1900
thí
sinh đỗ vào trường THPT gồm THPT chuyên và THPT không chuyên. Biết rằng trong đó có
61
thí sinh
đạt tổng điểm xét tuyển ba môn từ
44,0
điểm trở lên thì trường THPT chuyên đạt tỉ lệ
15%
và trường
THPT không chuyên đạt tỉ lệ
1%
. Hãy tính số thí sinh của thị xã đỗ vào mỗi trường: THPT chuyên và
THPT không chuyên trong kỳ thi này.
2) Năm
2025
, nhân kỷ niệm
135
năm ngày sinh của Chủ tịch Hồ Chí Minh, Lan và gia đình vào
thăm quê Bác trên một chuyến xe du lịch từ Hà Nội đến Nghệ An cách nhau
336
km trong một thời gian
đã định. Đi được
1
giờ
30
phút thì xe nghỉ, nhưng vì thời gian nghỉ quá
30
phút so với dự định nên để
đến nơi đúng thời gian đã định, xe phải tăng tốc thêm
7
km mỗi giờ. Tính vận tốc lúc đầu của xe. (Giả
định xe đi luôn tuân thủ luật giao thông và đảm bảo an toàn).
2
3) Biết rằng phương trình bậc hai
2
3 0
x mx
có một nghiệm là
5 13
2
x
và hai nghiệm
của phương trình này là độ dài hai cạnh góc vuông của một tam giác vuông. Tính cạnh huyền của tam
giác vuông đó.
Bài IV. (4,0 điểm)
1) Lương Thế Vinh nổi tiếng là thần đồng, học có phương pháp, vừa học vừa lao động, vui chơi
giải trí và được mệnh danh là “Trạng Lường”. Trong một lần chơi đá “bóng bưởi” cùng các bạn, bóng bị
rơi xuống một cái hố sâu và hẹp, Lương Thế Vinh cùng các bạn dùng nón múc nước đổ xuống hố cho đến
khi bóng nổi lên.
a) Biết nón có đường kính vành nón là
40
cm và chiều cao là
20
cm. Tính thể tích của nón.
b) Để lấy được bóng, Lương Thế Vinh cùng các bạn phải mất
10
lần đổ nón nước vào hố. Sau khi
bóng được lấy lên, mặt nước trong hố cách mặt đất
20
cm. Tính độ sâu của hố biết hố có dạng hình trụ
đường kính
20
cm và lượng nước dâng lên trong hố sau mỗi lần đổ một nón nước chỉ bằng
60%
thể tích
của nón. (Giả định lượng nước mỗi lần đổ vào hố là như nhau và trong quá trình đổ nước lấy bóng,
lượng nước thấm vào đất là không đáng kể).
(Lấy
3,14
và làm tròn kết quả đến hàng đơn vị).
2) Cho tam giác nhọn
ABC
(
AB AC
) nội tiếp đường tròn
O
và có các đường cao
AD
,
BE
,
CF
cắt nhau tại trực tâm
H
.
a) Chứng minh bốn điểm
A
,
F
,
D
,
C
cùng thuộc một đường tròn.
b) Gọi
M
là trung điểm của đoạn thẳng
BC
,
K
là giao điểm của hai đường thẳng
BC
và
EF
.
Chứng minh
FB
là tia phân giác của góc
DFK
và
. .
KD KM KE KF
.
c) Chứng minh
MF
là tiếp tuyến của đường tròn ngoại tiếp tam giác
KDF
.
Bài V. (0,5 điểm)
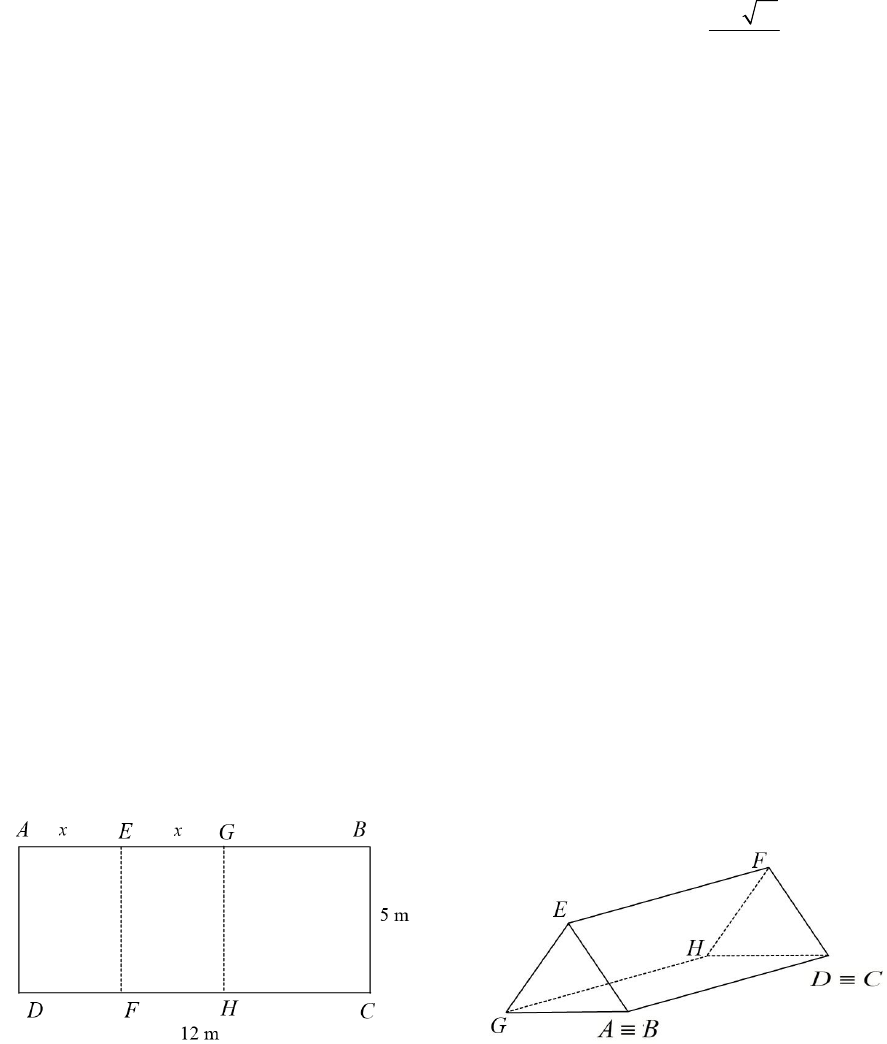
Bạn Hoa đi dã ngoại đã chuẩn bị một cái bạt hình chữ nhật
ABCD
có chiều dài
12
AB
m và
chiều rộng
5
BC
m để dựng thành một chiếc lều dạng hình lăng trụ đứng tam giác gồm hai mái lều và
đáy lều. Biết hai điểm
E
và
G
nằm trên cạnh
AB
sao cho
(m)
AE EG x
. Tìm
x
để thể tích không
gian trong lều là lớn nhất.
-------------------Hết------------------
(Cán bộ coi thi không giải thích gì thêm)
Họ và tên thí sinh:.......................................................................Số báo danh:...............................................
Họ và tên của cán bộ coi thi:......................................................Chữ ký của cán bộ coi thi:..........................

1
TRƯ
Ờ
NG THPT CHUYÊN SƠN TÂY
CÔNG TY CỔ PHẦN GIÁO DỤC FAMILY
ĐỀ KHẢO SÁT KIẾN THỨC KỲ THI TUYỂN SINH
LỚP 10 THPT (LẦN 2)
NĂM HỌC 2025 – 2026
HƯỚNG DẪN CHẤM MÔN TOÁN
(gồm 04 trang)
BÀI ĐÁP ÁN ĐIỂM
Bài I
1,5 điểm
1) Tìm tần số tương đối ghép nhóm và tần số ghép nhóm của nhóm có số học sinh
tự học nhiều nhất.
0,75
Nhóm có số học sinh tự học nhiều nhất là nhóm
1;2
có giá trị đại diện là
1,5
;
0,25
Nhóm này có tần số tương đối ghép nhóm là
66%
; 0,25
Và tần số ghép nhóm là:
350.66%
231
100%
(học sinh).
0,25
2) Tính xác suất của biến cố
A
: “Có ít nhất hai lần xuất hiện mặt ngửa”. 0,75
Không gian mẫu là:
{ ; ; ; ; ; ; ; }
SSS SSN SNS SNN NSS NSN NNS NNN
nên
8
n .
Vì
đ
ồng xu cân
đ
ối
đ
ồng chất nên c
ác k
ết quả có thể trên là
đ
ồng khả n
ăng.
0,25
Kết quả thuận lợi của biến cố
A
: “Có ít nhất hai lần xuất hiện mặt ngửa” là:
{ ; ; ; }
SNN NSN NNS NNN
nên
4
n A .
0,25
Xác suất của biến cố
A
là:
4 1
8 2
n A
P A
n
.
0,25
Bài II
1,5 điểm
1) Tính giá trị của biểu thức
A
khi
16
x
. 0,5
Thay
16
x
(thoả mãn điều kiện) vào biểu thức
A
, ta được: 0,25
16 2 14 7
4 2
16
A
.
0,25
2) Chứng minh
2
2
x
B
x
. 0,5
Với điều kiện
0, 4
x x
, ta có:
2 3 2
2 3 5 6 5 6
4
2
2 2 2 2
x x
x x x
B
x
x
x x x x
0,25
2 4
2 2
x x
x x
2 2
2
2
2 2
x x
x
x
x x
(đpcm).
0,25
3) Tìm tất cả các giá trị nguyên của
x
để biểu thức
P AB
có giá trị nguyên. 0,5
Với điều kiện
0, 4
x x
, ta có:
2 2
2 2
2 2
x
x x
P AB
x x x
. 0,25
Ta xét các trường hợp:
TH1: Với
2
x
(thỏa mãn điều kiện) thì
0
P
. Do đó
2
x
(thỏa mãn).
TH2: Với
x
nguyên dương,
2
x
,
4
x
và
x
không là số chính phương thì
x
là số
vô tỉ.
Khi đó:
2 2
x
là số nguyên khác
0
,
2
x
là số vô tỉ thì
2 2
2
x
P
x
là số vô tỉ
(không thỏa mãn).
TH3: Với
x
nguyên dương,
2
x
,
4
x
và
x
là số chính phương thì
x
là số nguyên.
0,25
Đề minh họa thi vào 10 môn Toán 2025
VnDoc giới thiệu đến quý thầy, cô giáo và các em học sinh Đề khảo sát Toán thi vào 10 lần 2 năm 2025 - 2026 trường chuyên Sơn Tây, Hà Nội. Đề thi với cấu trúc tự luận, thời gian làm bài 120 phút, mời các bạn thử sức.
Ngoài tài liệu trên, VnDoc còn gửi tới các bạn nhiều tài liệu tuyển sinh vào lớp 10 các môn để giúp các em ôn luyện, làm quen với nhiều đề thi khác nhau, chuẩn bị cho kì thi tuyển sinh vào lớp 10 năm học 2025 - 2026.



