Đề thi thử Toán vào 10 lần 4 trường THCS Nhữ Bá Sỹ, Thanh Hóa năm 2025 - 2026
Ôn thi vào lớp 10 môn Toán có đáp án
Lớp:
Ôn vào 10
Môn:
Toán
Dạng tài liệu:
Đề thi
Loại:
Tài liệu Lẻ
Loại File:
PDF
Phân loại:
Tài liệu Tính phí
UBND HUYỆN HOẰNG HÓA
TRƯỜNG THCS NHỮ BÁ SỸ
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT
NĂM HỌC 2025 - 2026
Môn: TOÁN
Thời gian làm bài: 120 phút, không kể thời gian giao đề
(Đề thi gồm có 02 trang)
Ngày thi: 09/03/2025
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm, gồm 08 câu, mỗi câu 0,25 điểm).
Câu 1. Phương trình
5 3 0x x
có nghiệm là:
A. x = -5 B. x = 3 C. x = -5 và x = 3 D. x = -5 hoặc x = 3
Câu 2. Điều kiện xác định của căn thức là:
Câu 3. Đồ thị hàm số nào sau đây đi qua điểm M(2; -2) ?
A.
2
1
2
y x
B.
2
1
2
y x
C.
2
2y x
D.
2
2y x
Câu 4. Nghiệm của bất phương trình
5( 2) 2 2x x
là:
A.
4.x
B.
4.x
C.
4.x
D.
4.x
Câu 5. Cho tam giác
ABC
vuông tại A, đường cao AH
6 , 9AB cm HC cm
. Độ dài cạnh AC là:
A.
3 6cm
B.
6 3cm
C.
5 3cm
D.
3 5cm
Câu 6. Trên đường tròn (O; 5cm) vẽ dây MN = 8cm. Khoảng cách từ tâm O đến dây MN là:
A. 3cm B. 4cm C. 5cm D. 8cm
Câu 7: Gieo 1 con xúc sắc 30 lần và được kết quả như sau:
Số chấm xuất hiện
1
2
3
4
5
6
Tần số
4
7
5
?
4
6
Tần số xuất hiện mặt 4 chấm là:
A.
2
B.
3
C.
4
D.
5
Câu 8. Xét phép thử ngẫu nhiên là việc gieo hai con xúc xắc cùng một lúc. Xác suất của biến cố:
“Tổng số chấm xuất hiện trên mặt hai con xúc xắc bằng 6” là:
A.
5
36
B.
11
36
C.
25
36
D.
31
36
PHẦN II. TỰ LUẬN (8,0 điểm).
Câu 9. (1,5 điểm)
a) (0,75 điểm). Giải phương trình:
2
3 5 2 0x x
b) (0,75 điểm). Giải hệ phương trình:
2 3 5
2 4
x y
x y
Câu 10. (1,0 điểm) Rút gọn biểu thức:
2 1 4 8 2
.
4
2 2 3
x x x x
A
x
x x x
với
0; 4; 9.x x x
Câu 11. (1,0 điểm) Cho phương trình
2
7 1 0x x m
(m là tham số). Tìm m để phương
trình đã cho có hai nghiệm dương phân biệt
1 2
,x x
thỏa mãn:
2
1 2 2
6 1 3x x x m
ĐỀ THI THỬ LẦN 4
Câu 12. (1 điểm) Hai vòi nước cùng chảy vào một bể cạn (bể không có nước) thì sau
4
3
giờ thì đầy bể. Nếu mở vòi I trong 20 phút và vòi II trong 30 phút thì chảy được
7
24
bể
nước. Hỏi nếu chảy riêng thì mỗi vòi chảy đầy bể trong bao lâu ?
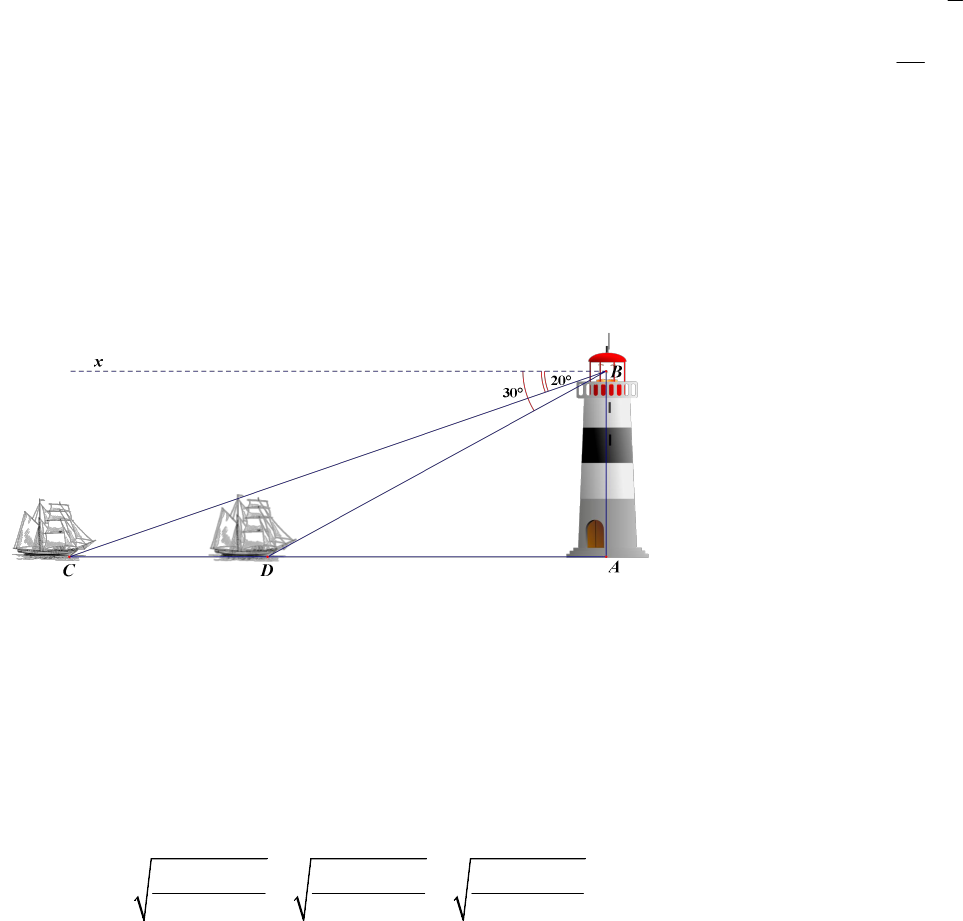
Câu 13 (1,0 điểm) Một người đứng trên tháp (tại
B
) của ngọn hải đăng ở độ cao 75 m
quan sát hai lần một con tàu đang hướng về ngọn hải đăng. Lần thứ nhất người đó nhìn
thấy tàu tại
C
với góc hạ là
20
, lần thứ 2 người đó nhìn thấy tàu tại
D
với góc hạ là
30
.
Hỏi con tàu đã đi được bao nhiêu mét giữa hai lần quan sát ? (kết quả làm tròn đến hàng
phần mười).
Câu 14. (2,0 điểm)
Cho nửa đường tròn (O) đường kính BC. Trên cung BC lấy các điểm F,
E (F thuộc cung BE; E, F khác B và C); đường thẳng BF và CE cắt nhau tại A; BE và CF
cắt nhau tại H; đường thẳng AH cắt EF và BC lần lượt tại I và D. Đường thẳng qua I song
song với BC cắt
,AB BE
lần lượt tại P, Q. Tia AQ cắt BC tại K.
a) Chứng minh các tứ giác AEHF , ACDF là tứ giác nội tiếp.
b) Chứng minh
. .AI HD AD HI
và D là trung điểm của BK.
Câu 15. (0,5 điểm) Cho các số thực dương
, ,a b c
thỏa mãn
2 2 2
1a b c
. Chứng minh:
2 2 2
2 2 2
2 2 2
2
1 1 1
ab c bc a ca b
ab bc ca
ab c bc a ca b
----------------Hết---------------
75m

HƯỚNG DẪN CHẤM
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm, gồm 08 câu, mỗi câu 0,25 điểm).
Câu
1
2
3
4
5
6
7
8
Đáp án
C
D
B
D
B
A
C
A
PHẦN II. TỰ LUẬN (8,0 điểm).
Câu
Nội dung
Điểm
Câu
9a.
a) Giải phương trình:
2
3 5 2 0x x
Phương trình là phương trình bậc hai có:
2
5 4.3.( 2) 49 0 7
0,25
Vậy phương trình có hai nghiệm phân biệt:
1 2
5 7 1 5 7
; 2
2.3 3 2.3
x x
0,5
Câu
9b.
Giải hệ phương trình:
2 3 5 2 3 5
2 4 2 4 8
x y x y
x y x y
0,25
3 2
2 12 8 3
y x
x y
0,25
Vậy hệ phương trình có 1 nghiệm duy nhất: (x, y) = (-2; 3)
0,25
Câu 10
Rút gọn biểu thức:
với
0; 4; 9.x x x
1,0
Với
0; 4; 9x x x
biểu thức A xác định. Ta có:
0,25
0,25
0,25
Vậy với
0,25
Câu 11
Cho phương trình
2
7 1 0x x m
(m là tham số). Tìm m để
phương trình đã cho có hai nghiệm dương phân biệt
1 2
,x x
thỏa
mãn:
2
1 2 2
6 1 3x x x m
1,0
Phương trình có hai nghiệm dương phân biệt
1 2
,x x
khi và chỉ khi:
0,25
Đề minh họa thi vào 10 môn Toán 2025
VnDoc giới thiệu đến quý thầy, cô giáo và các em học sinh Đề thi thử Toán vào 10 lần 4 trường THCS Nhữ Bá Sỹ, Thanh Hóa năm 2025 - 2026. Tài liệu với cấu trúc trắc nghiệm và tự luận, có đáp án và hướng dẫn giải cho các em so sánh và đối chiếu với bài làm của mình.
Ngoài tài liệu trên, VnDoc còn gửi tới các bạn nhiều tài liệu tuyển sinh vào lớp 10 các môn để giúp các em ôn luyện, làm quen với nhiều đề thi khác nhau, chuẩn bị cho kì thi tuyển sinh vào lớp 10 năm học 2025 - 2026.




