Giải SBT Toán 12 bài 6: Bất phương trình mũ và bất phương trình logarit

Giải SBT Toán lớp 12

Toán 12 - Bất phương trình mũ và bất phương trình logarit

Để giúp các bạn học sinh có kết quả cao hơn trong học tập, VnDoc mời các bạn tham khảo tài liệu Giải SBT Toán 12 bài 6: Bất phương trình mũ và bất phương trình logarit, với nội dung được cập nhật chi tiết và chính xác sẽ là nguồn thông tin hay để giúp các bạn học sinh học tốt hơn môn Toán 12.

Giải SBT Toán 12 bài 2: Hàm số lũy thừa

Giải SBT Toán 12 bài 3: Logarit

Giải SBT Toán 12 bài 4: Hàm số mũ. Hàm số logarit

Giải SBT Toán 12 bài 5: Phương trình mũ và phương trình logarit

Giải SBT Toán 12 bài 6

Bài 2.39 trang 131, 132 Sách bài tập (SBT) Giải tích 12

Giải các bất phương trình mũ sau:

a) ${3^{|x - 2|}} < 9$ ${3^{|x - 2|}} < 9$

b) ${4^{|x + 1|}} > 16$ ${4^{|x + 1|}} > 16$

c) ${2^{ - {x^2} + 3x}} < 4$ ${2^{ - {x^2} + 3x}} < 4$

d) ${(\frac{7}{9})^{2{x^2} - 3x}} \ge \frac{9}{7}$ ${(\frac{7}{9})^{2{x^2} - 3x}} \ge \frac{9}{7}$

e) ${11^{\sqrt {x + 6} }} \ge {11^x}$ ${11^{\sqrt {x + 6} }} \ge {11^x}$

g) ${2^{2x - 1}} + {2^{2x - 2}} + {2^{2x - 3}} \ge 448$ ${2^{2x - 1}} + {2^{2x - 2}} + {2^{2x - 3}} \ge 448$

h) ${16^x} - {4^x} - 6 \le 0$ ${16^x} - {4^x} - 6 \le 0$

i) $\frac{{{3^x}}}{{{3^x} - 2}} < 3$ $\frac{{{3^x}}}{{{3^x} - 2}} < 3$

Hướng dẫn làm bài:

a) ${3^{|x - 2|}} < {3^2}$ ${3^{|x - 2|}} < {3^2}$

$\Leftrightarrow |x - 2| < 2$ $\Leftrightarrow |x - 2| < 2$

$\Leftrightarrow - 2 < x - 2 < 2$ $\Leftrightarrow - 2 < x - 2 < 2$

$\Leftrightarrow 0 < x < 4$ $\Leftrightarrow 0 < x < 4$

b)

${4^{|x + 1|}} > {4^2} \Leftrightarrow |x + 1| > 2 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x + 1 > 2}\\ {x + 1 < - 2} \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x > 1}\\ {x < - 3} \end{array}} \right.$ ${4^{|x + 1|}} > {4^2} \Leftrightarrow |x + 1| > 2 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x + 1 > 2}\\ {x + 1 < - 2} \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x > 1}\\ {x < - 3} \end{array}} \right.$

c)

${2^{ - {x^2} + 3x}} < {2^2}$ ${2^{ - {x^2} + 3x}} < {2^2}$

$\Leftrightarrow - {x^2} + 3x < 2 \Leftrightarrow {x^2} - 3x + 2 > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x < 1}\\ {x > 2} \end{array}} \right.$ $\Leftrightarrow - {x^2} + 3x < 2 \Leftrightarrow {x^2} - 3x + 2 > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x < 1}\\ {x > 2} \end{array}} \right.$

d)

${(\frac{7}{9})^{2{x^2} - 3x}} \ge {(\frac{7}{9})^{ - 1}}$ ${(\frac{7}{9})^{2{x^2} - 3x}} \ge {(\frac{7}{9})^{ - 1}}$

$\Leftrightarrow 2{x^2} - 3x \le - 1$ $\Leftrightarrow 2{x^2} - 3x \le - 1$

$\Leftrightarrow 2{x^2} - 3x + 1 \le 0 \Leftrightarrow \frac{1}{2} \le x \le 1$ $\Leftrightarrow 2{x^2} - 3x + 1 \le 0 \Leftrightarrow \frac{1}{2} \le x \le 1$

e)

$\eqalign{& \sqrt {x + 6} \ge x \Leftrightarrow \left[ {\matrix{{\left\{ {\matrix{{x + 6 \ge 0} \cr {x < 0} \cr} } \right.} \cr {\left\{ {\matrix{{x \ge 0} \cr {x + 6 \ge {x^2}} \cr} } \right.} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{\left\{ {\matrix{{x \ge - 6} \cr {x < 0} \cr} } \right.} \cr {\left\{ {\matrix{{x \ge 0} \cr {{x^2} - x - 6 \le 0} \cr} } \right.} \cr} } \right. \Leftrightarrow \left[ {\matrix{{ - 6 \le x < 0} \cr {\left\{ {\matrix{{ - 2 \le x \le 3} \cr {x \ge 0} \cr} } \right.} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{ - 6 \le x < 0} \cr {0 \le x \le 3} \cr} } \right. \Leftrightarrow - 6 \le x \le 3 \cr}$ $\eqalign{& \sqrt {x + 6} \ge x \Leftrightarrow \left[ {\matrix{{\left\{ {\matrix{{x + 6 \ge 0} \cr {x < 0} \cr} } \right.} \cr {\left\{ {\matrix{{x \ge 0} \cr {x + 6 \ge {x^2}} \cr} } \right.} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{\left\{ {\matrix{{x \ge - 6} \cr {x < 0} \cr} } \right.} \cr {\left\{ {\matrix{{x \ge 0} \cr {{x^2} - x - 6 \le 0} \cr} } \right.} \cr} } \right. \Leftrightarrow \left[ {\matrix{{ - 6 \le x < 0} \cr {\left\{ {\matrix{{ - 2 \le x \le 3} \cr {x \ge 0} \cr} } \right.} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{ - 6 \le x < 0} \cr {0 \le x \le 3} \cr} } \right. \Leftrightarrow - 6 \le x \le 3 \cr}$

g)

$\frac{1}{2}{.2^{2x}} + \frac{1}{4}{.2^{2x}} + \frac{1}{8}{.2^{2x}} \ge 448$ $\frac{1}{2}{.2^{2x}} + \frac{1}{4}{.2^{2x}} + \frac{1}{8}{.2^{2x}} \ge 448$

$\Leftrightarrow {2^{2x}} \ge 512 \Leftrightarrow {2^{2x}} \ge {2^9} \Leftrightarrow x \ge \frac{9}{2}$ $\Leftrightarrow {2^{2x}} \ge 512 \Leftrightarrow {2^{2x}} \ge {2^9} \Leftrightarrow x \ge \frac{9}{2}$

h) Đặt t = 4^x (t > 0), ta có hệ bất phương trình:

$\eqalign{& \left\{ {\matrix{{{t^2} - t - 6 \le 0} \cr {t > 0} \cr} } \right. \Leftrightarrow \left\{ {\matrix{{ - 2 \le t \le 3} \cr {t > 0} \cr} } \right. \cr & \Leftrightarrow 0 < t \le 3 \Leftrightarrow 0 < {4^x} \le 3 \Leftrightarrow x \le {\log _4}3 \cr}$ $\eqalign{& \left\{ {\matrix{{{t^2} - t - 6 \le 0} \cr {t > 0} \cr} } \right. \Leftrightarrow \left\{ {\matrix{{ - 2 \le t \le 3} \cr {t > 0} \cr} } \right. \cr & \Leftrightarrow 0 < t \le 3 \Leftrightarrow 0 < {4^x} \le 3 \Leftrightarrow x \le {\log _4}3 \cr}$

i)

$\eqalign{& {{{3^x}} \over {{3^x} - 2}} - 3 < 0 \Leftrightarrow {{ - {{2.3}^x} + 6} \over {{3^x} - 2}} < 0 \cr & \Leftrightarrow {{{3^x} - 3} \over {{3^x} - 2}} > 0 \Leftrightarrow \left[ {\matrix{{{3^x} > 3} \cr {{3^x} < 2} \cr} } \right. \Leftrightarrow \left[ {\matrix{{x > 1} \cr {x < {{\log }_3}2} \cr} } \right. \cr}$ $\eqalign{& {{{3^x}} \over {{3^x} - 2}} - 3 < 0 \Leftrightarrow {{ - {{2.3}^x} + 6} \over {{3^x} - 2}} < 0 \cr & \Leftrightarrow {{{3^x} - 3} \over {{3^x} - 2}} > 0 \Leftrightarrow \left[ {\matrix{{{3^x} > 3} \cr {{3^x} < 2} \cr} } \right. \Leftrightarrow \left[ {\matrix{{x > 1} \cr {x < {{\log }_3}2} \cr} } \right. \cr}$

Bài 2.40 trang 132 Sách bài tập (SBT) Giải tích 12

Giải các bất phương trình logarit sau:

a) ${\log _{\frac{1}{3}}}(x - 1) \ge - 2$ ${\log _{\frac{1}{3}}}(x - 1) \ge - 2$

b) ${\log _3}(x - 3) + {\log _3}(x - 5) < 1$ ${\log _3}(x - 3) + {\log _3}(x - 5) < 1$

c) ${\log _{\frac{1}{2}}}\frac{{2{x^2} + 3}}{{x - 7}} < 0$ ${\log _{\frac{1}{2}}}\frac{{2{x^2} + 3}}{{x - 7}} < 0$

d) ${\log _{\frac{1}{3}}}{\log _2}{x^2} > 0$ ${\log _{\frac{1}{3}}}{\log _2}{x^2} > 0$

e) $\frac{1}{{5 - \log x}} + \frac{2}{{1 + \log x}} < 1$ $\frac{1}{{5 - \log x}} + \frac{2}{{1 + \log x}} < 1$

g) $4{\log _4}x - 33{\log _x}4 \le 1$ $4{\log _4}x - 33{\log _x}4 \le 1$

Hướng dẫn làm bài:

a) $0 < x - 1 \le {(\frac{1}{3})^{ - 2}} \Leftrightarrow 1 < x \le 10$ $0 < x - 1 \le {(\frac{1}{3})^{ - 2}} \Leftrightarrow 1 < x \le 10$

b)

$\eqalign{& \left\{ {\matrix{{x > 5} \cr {{{\log }_3}{\rm{[}}(x - 3)(x - 5){\rm{]}} < {{\log }_3}3} \cr} } \right. \cr & \Leftrightarrow \left\{ {\matrix{{x > 5} \cr {{x^2} - 8x + 12 < 0} \cr} \Leftrightarrow \left\{ {\matrix{{x > 5} \cr {2 < x < 6} \cr} } \right.} \right. \cr & \Leftrightarrow 5 < x < 6 \cr}$ $\eqalign{& \left\{ {\matrix{{x > 5} \cr {{{\log }_3}{\rm{[}}(x - 3)(x - 5){\rm{]}} < {{\log }_3}3} \cr} } \right. \cr & \Leftrightarrow \left\{ {\matrix{{x > 5} \cr {{x^2} - 8x + 12 < 0} \cr} \Leftrightarrow \left\{ {\matrix{{x > 5} \cr {2 < x < 6} \cr} } \right.} \right. \cr & \Leftrightarrow 5 < x < 6 \cr}$

c)

$\eqalign{& \left\{ {\matrix{{x - 7 > 0} \cr {{{2{x^2} + 3} \over {x - 7}} > 1} \cr} \Leftrightarrow \left\{ {\matrix{{x > 7} \cr {2{x^2} + 3 > x - 7} \cr} } \right.} \right. \cr & \Leftrightarrow \left\{ {\matrix{{x > 7} \cr {2{x^2} - x + 10 > 0} \cr} \Leftrightarrow \left\{ {\matrix{{x > 7} \cr {x \in R} \cr} \Leftrightarrow x > 7} \right.} \right. \cr}$ $\eqalign{& \left\{ {\matrix{{x - 7 > 0} \cr {{{2{x^2} + 3} \over {x - 7}} > 1} \cr} \Leftrightarrow \left\{ {\matrix{{x > 7} \cr {2{x^2} + 3 > x - 7} \cr} } \right.} \right. \cr & \Leftrightarrow \left\{ {\matrix{{x > 7} \cr {2{x^2} - x + 10 > 0} \cr} \Leftrightarrow \left\{ {\matrix{{x > 7} \cr {x \in R} \cr} \Leftrightarrow x > 7} \right.} \right. \cr}$

d)

$\eqalign{ & {\log _{{1 \over 3}}}{\log _2}{x^2} > {\log _{{1 \over 3}}}1 \cr & \Leftrightarrow {\log _2}{x^2} < 1 \cr & \Leftrightarrow {\log _2}{x^2} < {\log _2}2 \cr & \Leftrightarrow 0 < {x^2} < 2 \cr}$ $\eqalign{ & {\log _{{1 \over 3}}}{\log _2}{x^2} > {\log _{{1 \over 3}}}1 \cr & \Leftrightarrow {\log _2}{x^2} < 1 \cr & \Leftrightarrow {\log _2}{x^2} < {\log _2}2 \cr & \Leftrightarrow 0 < {x^2} < 2 \cr}$

$\Leftrightarrow 0 < |x| < \sqrt 2 \Leftrightarrow \left[ {\matrix{{ - \sqrt 2 < x < 0} \cr {0 < x < \sqrt 2 } \cr} } \right.$ $\Leftrightarrow 0 < |x| < \sqrt 2 \Leftrightarrow \left[ {\matrix{{ - \sqrt 2 < x < 0} \cr {0 < x < \sqrt 2 } \cr} } \right.$

e) Đặt $t = \log x$ $t = \log x$ với điều kiện $t \ne 5,t \ne - 1$ $t \ne 5,t \ne - 1$ ta có:

$\eqalign{ & {1 \over {5 - t}} + {2 \over {1 + t}} < 1 \Leftrightarrow {{t + 1 + 10 - 2t} \over {5 + 4t - {t^2}}} - 1 < 0 \cr & \Leftrightarrow {{{t^2} - 5t + 6} \over {{t^2} - 4t - 5}} > 0 \Leftrightarrow {{(t - 2)(t - 3)} \over {(t + 1)(t - 5)}} > 0 \cr & \Leftrightarrow \left[ {\matrix{{t < - 1} \cr {2 < t < 3} \cr {t > 5} \cr} } \right. \cr}$ $\eqalign{ & {1 \over {5 - t}} + {2 \over {1 + t}} < 1 \Leftrightarrow {{t + 1 + 10 - 2t} \over {5 + 4t - {t^2}}} - 1 < 0 \cr & \Leftrightarrow {{{t^2} - 5t + 6} \over {{t^2} - 4t - 5}} > 0 \Leftrightarrow {{(t - 2)(t - 3)} \over {(t + 1)(t - 5)}} > 0 \cr & \Leftrightarrow \left[ {\matrix{{t < - 1} \cr {2 < t < 3} \cr {t > 5} \cr} } \right. \cr}$

Suy ra log x < -1 hoặc 2 < log x < 3 hoặc log x > 5.

Vậy $x < \frac{1}{{10}}$ $x < \frac{1}{{10}}$ hoặc 100 < x < 1000 hoặc x > 100 000.

g) Với điều kiện $x > 0,x \ne 1$ $x > 0,x \ne 1$ đặt $t = {\log _4}x$ $t = {\log _4}x$, ta có: $4t - \frac{{33}}{t} \le 1$ $4t - \frac{{33}}{t} \le 1$

$\eqalign{& \Leftrightarrow {{4{t^2} - t - 33} \over t} \le 0 \Leftrightarrow {{(4t + 11)(t - 3)} \over t} \le 0 \cr & \Leftrightarrow \left[ {\matrix{{t \le - {{11} \over 4}} \cr {0 < t \le 3} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{{{\log }_4}x \le - {{11} \over 4}} \cr {0 < {{\log }_4}x \le 3} \cr} } \right. \Leftrightarrow \left[ {\matrix{{0 < x \le {4^{ - {{11} \over 4}}}} \cr {1 < x \le 64} \cr} } \right. \cr}$ $\eqalign{& \Leftrightarrow {{4{t^2} - t - 33} \over t} \le 0 \Leftrightarrow {{(4t + 11)(t - 3)} \over t} \le 0 \cr & \Leftrightarrow \left[ {\matrix{{t \le - {{11} \over 4}} \cr {0 < t \le 3} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{{{\log }_4}x \le - {{11} \over 4}} \cr {0 < {{\log }_4}x \le 3} \cr} } \right. \Leftrightarrow \left[ {\matrix{{0 < x \le {4^{ - {{11} \over 4}}}} \cr {1 < x \le 64} \cr} } \right. \cr}$

Bài 2.41 trang 132 Sách bài tập (SBT) Giải tích 12

Giải các bất phương trình sau bằng đồ thị:

a) ${(\frac{1}{2})^x} < x - \frac{1}{2}$ ${(\frac{1}{2})^x} < x - \frac{1}{2}$

b) ${(\frac{1}{3})^x} \ge x + 1$ ${(\frac{1}{3})^x} \ge x + 1$

c) ${\log _{\frac{1}{3}}}x > 3x$ ${\log _{\frac{1}{3}}}x > 3x$

d) ${\log _2}x \le 6 - x$ ${\log _2}x \le 6 - x$

Hướng dẫn làm bài:

a) Vẽ đồ thị của hàm số $y = {(\frac{1}{2})^x}$ $y = {(\frac{1}{2})^x}$ và đường thẳng $y = x - \frac{1}{2}$ $y = x - \frac{1}{2}$ trên cùng một hệ trục tọa độ (H.65), ta thấy chúng cắt nhau tại điểm có hoành độ x = 1. Với x > 1 đồ thị của hàm số $y = {(\frac{1}{2})^x}$ $y = {(\frac{1}{2})^x}$ nằm phía dưới đường thẳng $y = x - \frac{1}{2}$ $y = x - \frac{1}{2}$. Vậy tập nghiệm của bất phương trình đã cho là $(1; + \infty )$ $(1; + \infty )$

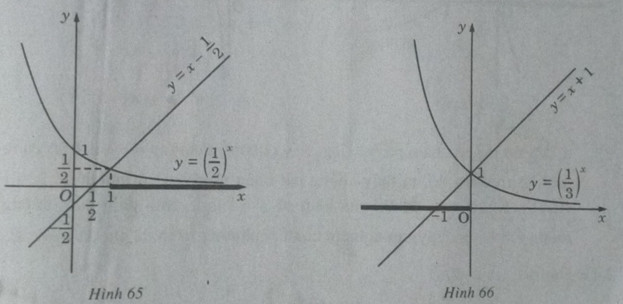
Giải SBT Toán 12 bài 6: Bất phương trình mũ và bất phương trình logarit

b) Vẽ đồ thị của hàm số $y = {(\frac{1}{3})^x}$ $y = {(\frac{1}{3})^x}$ và đường thẳng y = x + 1 trên cùng một hệ trục tọa độ (H.66), ta thấy chúng cắt nhau tại điểm có hoành độ x = 0.

Khi x < 0 đồ thị của hàm số $y = {(\frac{1}{3})^x}$ $y = {(\frac{1}{3})^x}$nằm phía trên đường thẳng y = x + 1. Vậy tập nghiệm của bất phương trình đã cho là $( - \infty ;0]$ $( - \infty ;0]$

c) Vẽ đồ thị của hàm số $y = {\log _{\frac{1}{3}}}x$ $y = {\log _{\frac{1}{3}}}x$ và đường thẳng y = 3x trên cùng một hệ trục tọa độ ta thấy chúng cắt nhau tại điểm có hoành độ $x = \frac{1}{3}$ $x = \frac{1}{3}$ (H.67)

Khi $x < \frac{1}{3}$ $x < \frac{1}{3}$ đồ thị của hàm số $y = {\log _{\frac{1}{3}}}x$ $y = {\log _{\frac{1}{3}}}x$ nằm phía trên đường thẳng y = 3x.

Vậy tập nghiệm của bất phương trình đã cho là $( - \infty ;\frac{1}{3})$ $( - \infty ;\frac{1}{3})$.

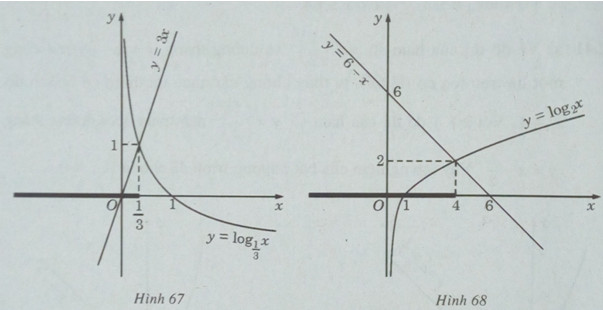
Giải SBT Toán 12 bài 6: Bất phương trình mũ và bất phương trình logarit

d) Vẽ đồ thị của hàm số y=log₂x và đường thẳng y = 6 – x trên cùng một hệ trục tọa độ, ta thấy chúng cắt nhau tại điểm có hoành độ x = 4 (H.68).

Khi x < 4, đồ thị của hàm số y=log₂x nằm phía dưới y = 6 – x.

Vậy tập nghiệm của bất phương trình đã cho là $(−∞;4]$

Bài 2.42 trang 132 Sách bài tập (SBT) Giải tích 12

Giải bất phương trình: ${\log _{\frac{1}{3}}}({\log _2}\frac{{2x + 3}}{{x + 1}}) \ge 0$ ${\log _{\frac{1}{3}}}({\log _2}\frac{{2x + 3}}{{x + 1}}) \ge 0$

Trả lời:

Đáp số: x < - 2.

---------------------------------

Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải SBT Toán 12 bài 6: Bất phương trình mũ và bất phương trình logarit. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán lớp 12, Giải bài tập Hóa học lớp 12, Giải bài tập Vật Lí 12 mà VnDoc tổng hợp và đăng tải.

Chia sẻ, đánh giá bài viết

1

313

Bài trước

Bài sau