VnDoc.com

Giải SBT Toán 12 bài 5: Phương trình mũ và phương trình logarit

Giải SBT Toán lớp 12

Bài trước

Bài sau

Toán 12 - Phương trình mũ và phương trình logarit

Để rèn luyện giải bài tập Toán nhanh và hiệu quả hơn, VnDoc mời các bạn học sinh tham khảo tài liệu Giải SBT Toán 12 bài 5: Phương trình mũ và phương trình logarit, chắc chắn nội dung tài liệu sẽ giúp các bạn học sinh đạt kết quả cao hơn trong học tập.

Giải SBT Toán 12 bài 1: Lũy thừa

Giải SBT Toán 12 bài 2: Hàm số lũy thừa

Giải SBT Toán 12 bài 3: Logarit

Giải SBT Toán 12 bài 5

Bài 2.30 trang 125 Sách bài tập (SBT) Giải tích 12

Giải các phương trình mũ sau:

a) ${(0,75)^{2x - 3}} = {(1\frac{1}{3})^{5 - x}}$ ${(0,75)^{2x - 3}} = {(1\frac{1}{3})^{5 - x}}$

b) ${5^{{x^2} - 5x - 6}} = 1$ ${5^{{x^2} - 5x - 6}} = 1$

c) ${(\frac{1}{7})^{{x^2} - 2x - 3}} = {7^{x + 1}}$ ${(\frac{1}{7})^{{x^2} - 2x - 3}} = {7^{x + 1}}$

d) ${32^{\frac{{x + 5}}{{x - 7}}}} = 0,{25.125^{\frac{{x + 17}}{{x - 3}}}}$ ${32^{\frac{{x + 5}}{{x - 7}}}} = 0,{25.125^{\frac{{x + 17}}{{x - 3}}}}$

Hướng dẫn làm bài:

a) ${(\frac{3}{4})^{2x - 3}} = {(\frac{4}{3})^{5 - x}}$ ${(\frac{3}{4})^{2x - 3}} = {(\frac{4}{3})^{5 - x}}$

$\Leftrightarrow {(\frac{3}{4})^{2x - 3}} = {(\frac{3}{4})^{x - 5}}$ $\Leftrightarrow {(\frac{3}{4})^{2x - 3}} = {(\frac{3}{4})^{x - 5}}$

$\Leftrightarrow 2x - 3 = x - 5 \Leftrightarrow x = - 2$ $\Leftrightarrow 2x - 3 = x - 5 \Leftrightarrow x = - 2$

b)

$\begin{array}{l} {5^{{x^2} - 5x - 6}} = {5^0} \Leftrightarrow {x^2} - 5x - 6 = 0\\ \Leftrightarrow \left[ \begin{array}{l} x = - 1\\ x = 6 \end{array} \right. \end{array}$ $\begin{array}{l} {5^{{x^2} - 5x - 6}} = {5^0} \Leftrightarrow {x^2} - 5x - 6 = 0\\ \Leftrightarrow \left[ \begin{array}{l} x = - 1\\ x = 6 \end{array} \right. \end{array}$

c)

$\begin{array}{l} {(\frac{1}{7})^{{x^2} - 2x - 3}} = {(\frac{1}{7})^{ - x - 1}} \Leftrightarrow {x^2} - 2x - 3 = - x - 1 \Leftrightarrow {x^2} - x - 2 = 0\\ \Leftrightarrow \left[ \begin{array}{l} x = - 1\\ x = 2 \end{array} \right. \end{array}$ $\begin{array}{l} {(\frac{1}{7})^{{x^2} - 2x - 3}} = {(\frac{1}{7})^{ - x - 1}} \Leftrightarrow {x^2} - 2x - 3 = - x - 1 \Leftrightarrow {x^2} - x - 2 = 0\\ \Leftrightarrow \left[ \begin{array}{l} x = - 1\\ x = 2 \end{array} \right. \end{array}$

d) ${2^{5.\frac{{x + 5}}{{x - 7}}}} = {2^{ - 2}}{.5^{3.\frac{{x + 17}}{{x - 3}}}} < = > {2^{\frac{{5x + 25}}{{x - 7}} + 2}} = {5^{\frac{{3x + 51}}{{x - 3}}}} < = > {2^{\frac{{7x + 11}}{{x - 7}}}} = {5^{\frac{{3x + 51}}{{x - 3}}}}$ ${2^{5.\frac{{x + 5}}{{x - 7}}}} = {2^{ - 2}}{.5^{3.\frac{{x + 17}}{{x - 3}}}} < = > {2^{\frac{{5x + 25}}{{x - 7}} + 2}} = {5^{\frac{{3x + 51}}{{x - 3}}}} < = > {2^{\frac{{7x + 11}}{{x - 7}}}} = {5^{\frac{{3x + 51}}{{x - 3}}}}$

Lấy logarit cơ số 2 cả hai vế, ta được:

$\frac{{7x + 11}}{{x - 7}} = \frac{{3x + 51}}{{x - 3}}{\log _2}5 < = > \left\{ {\begin{array}{*{20}{c}} {7{x^2} - 10x - 33 = (3{x^2} + 30x - 357){{\log }_2}5}\\ {x \ne 7,x \ne 3} \end{array}} \right.$ $\frac{{7x + 11}}{{x - 7}} = \frac{{3x + 51}}{{x - 3}}{\log _2}5 < = > \left\{ {\begin{array}{*{20}{c}} {7{x^2} - 10x - 33 = (3{x^2} + 30x - 357){{\log }_2}5}\\ {x \ne 7,x \ne 3} \end{array}} \right.$

$< = > (7 - 3{\log _2}5){x^2} - 2(5 + 15{\log _2}5) - (33 - 357{\log _2}5) = 0$ $< = > (7 - 3{\log _2}5){x^2} - 2(5 + 15{\log _2}5) - (33 - 357{\log _2}5) = 0$

Ta có: $\Delta$ $\Delta ' = {(5 + 15{\log _2}5)^2} + (7 - 3{\log _2}5)(33 - 357{\log _2}5)$

$= 1296\log _2^25 - 2448{\log _2}5 + 256 > 0$ $= 1296\log _2^25 - 2448{\log _2}5 + 256 > 0$

Phương trình đã cho có hai nghiệm: $x = \frac{{5 + 15{{\log }_2}5 \pm \sqrt {\Delta$ $x = \frac{{5 + 15{{\log }_2}5 \pm \sqrt {\Delta '} }}{{7 - 3{{\log }_2}5}}$, đều thỏa mãn điều kiện

Bài 2.31 trang 125 Sách bài tập (SBT) Giải tích 12

Giải các phương trình mũ sau:

a) ${2^{x + 4}} + {2^{x + 2}} = {5^{x + 1}} + {3.5^x}$ ${2^{x + 4}} + {2^{x + 2}} = {5^{x + 1}} + {3.5^x}$

b) ${5^{2x}} - {7^x} - {5^{2x}}.17 + {7^x}.17 = 0$ ${5^{2x}} - {7^x} - {5^{2x}}.17 + {7^x}.17 = 0$

c) ${4.9^x} + {12^x} - {3.16^x} = 0$ ${4.9^x} + {12^x} - {3.16^x} = 0$

d) $- {8^x} + {2.4^x} + {2^x} - 2 = 0$ $- {8^x} + {2.4^x} + {2^x} - 2 = 0$

Hướng dẫn làm bài:

a) ${16.2^x} + {4.2^x} = {5.5^x} + {3.5^x}$ ${16.2^x} + {4.2^x} = {5.5^x} + {3.5^x}$

$\Leftrightarrow {20.2^x} = {8.5^x} \Leftrightarrow {(\frac{2}{5})^x} = {(\frac{2}{5})^1} \Leftrightarrow x = 1$ $\Leftrightarrow {20.2^x} = {8.5^x} \Leftrightarrow {(\frac{2}{5})^x} = {(\frac{2}{5})^1} \Leftrightarrow x = 1$

b) ${16.7^x} - {16.5^{2x}} = 0$ ${16.7^x} - {16.5^{2x}} = 0$

$\Leftrightarrow {7^x} = {5^{2x}} \Leftrightarrow {(\frac{7}{{25}})^x} = {(\frac{7}{{25}})^0} \Leftrightarrow x = 0$ $\Leftrightarrow {7^x} = {5^{2x}} \Leftrightarrow {(\frac{7}{{25}})^x} = {(\frac{7}{{25}})^0} \Leftrightarrow x = 0$

c) Chia hai vế cho ${12^x}({12^x} > 0)$ ${12^x}({12^x} > 0)$, ta được:

$4{(\frac{3}{4})^x} + 1 - 3{(\frac{4}{3})^x} = 0$ $4{(\frac{3}{4})^x} + 1 - 3{(\frac{4}{3})^x} = 0$

Đặt $t = {(\frac{3}{4})^x}(t > 0)$ $t = {(\frac{3}{4})^x}(t > 0)$, ta có phương trình:

$4t + 1 - \frac{3}{t} = 0 \Leftrightarrow 4{t^2} + t - 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {t = - 1(l)}\\ {t = \frac{3}{4}} \end{array}} \right.$ $4t + 1 - \frac{3}{t} = 0 \Leftrightarrow 4{t^2} + t - 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {t = - 1(l)}\\ {t = \frac{3}{4}} \end{array}} \right.$

Do đó, ${(\frac{3}{4})^x} = {(\frac{3}{4})^1}$ ${(\frac{3}{4})^x} = {(\frac{3}{4})^1}$. Vậy x = 1.

d) Đặt $t = {2^x}(t > 0)$ $t = {2^x}(t > 0)$, ta có phương trình:

$- {t^3} + 2{t^2} + t - 2 = 0 \Leftrightarrow(t - 1)(t + 1)(2 - t) = 0 < = >\Leftrightarrow \left[ {\begin{array}{*{20}{c}} {t = 1}\\ {t = - 1(l)}\\ {t = 2} \end{array}} \right.$ $- {t^3} + 2{t^2} + t - 2 = 0 \Leftrightarrow(t - 1)(t + 1)(2 - t) = 0 < = >\Leftrightarrow \left[ {\begin{array}{*{20}{c}} {t = 1}\\ {t = - 1(l)}\\ {t = 2} \end{array}} \right.$

Do đó,

$\left[ {\begin{array}{*{20}{c}} {{2^x} = 1}\\ {{2^x} = 2} \end{array}} \right.$ $\left[ {\begin{array}{*{20}{c}} {{2^x} = 1}\\ {{2^x} = 2} \end{array}} \right.$

Bài 2.32 trang 125 Sách bài tập (SBT) Giải tích 12

Giải các phương trình sau bằng phương pháp đồ thị:

a) ${2^{ - x}} = 3x + 10$ ${2^{ - x}} = 3x + 10$

b) ${(\frac{1}{3})^{ - x}} = - 2x + 5$ ${(\frac{1}{3})^{ - x}} = - 2x + 5$

c) ${(\frac{1}{3})^x} = x + 1$ ${(\frac{1}{3})^x} = x + 1$

d) ${3^x} = 11 - x$ ${3^x} = 11 - x$

Hướng dẫn làm bài:

a) Vẽ đồ thị của hàm số: $y = {2^{ - x}}$ $y = {2^{ - x}}$ và đường thẳng y = 3x +10 trên cùng một hệ trục tọa độ (H. 57) ta thấy chúng cắt nhau tại điểm có hoành độ x = -2. Thử lại, ta thấy x = -2 thỏa mãn phương trình đã cho.

Mặt khác, hàm số $y = {2^{ - x}} = {(\frac{1}{2})^x}$ $y = {2^{ - x}} = {(\frac{1}{2})^x}$ luôn nghịch biến, hàm số y = 3x + 10 luôn đồng biến.

Vậy x = -2 là nghiệm duy nhất.

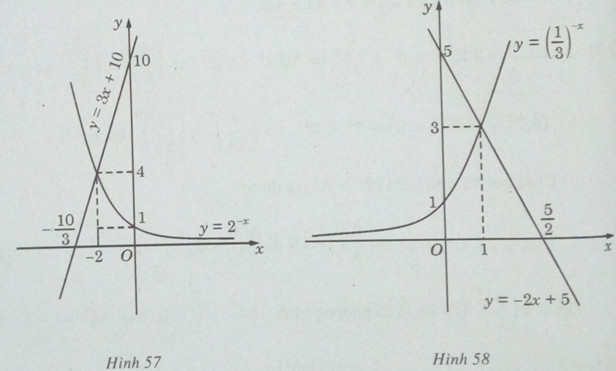
Giải SBT Toán 12 bài 5: Phương trình mũ và phương trình logarit

b) Vẽ đồ thị của hàm số $y = {(\frac{1}{3})^{ - x}}$ $y = {(\frac{1}{3})^{ - x}}$và đường thẳng y = -2x + 5 trên cùng một hệ trục tọa độ (H.58), ta thấy chúng cắt nhau tại điểm có hoành độ x = 1. Thử lại, ta thấy x = 1 thỏa mãn phương trình đã cho.

Mặt khác, hàm số $y = {(\frac{1}{3})^{ - x}} = {3^x}$ $y = {(\frac{1}{3})^{ - x}} = {3^x}$luôn đồng biến, hàm số y = -2x + 5 luôn nghịch biến.

Vậy x = 1 là nghiệm duy nhất.

c) Vẽ đồ thị của hàm số $y = {(\frac{1}{3})^x}$ $y = {(\frac{1}{3})^x}$ và đường thẳng y = x + 1 trên cùng một hệ trục tọa độ (H.59), ta thấy chúng cắt nhau tại điểm có hoành độ x = 0. Thử lại, ta thấy x = 0 thỏa mãn phương trình đã cho. Mặt khác, $y = {(\frac{1}{3})^x}$ $y = {(\frac{1}{3})^x}$ là hàm số luôn nghịch biến, hàm số y = x +1 luôn đồng biến.

Vậy x = 0 là nghiệm duy nhất.

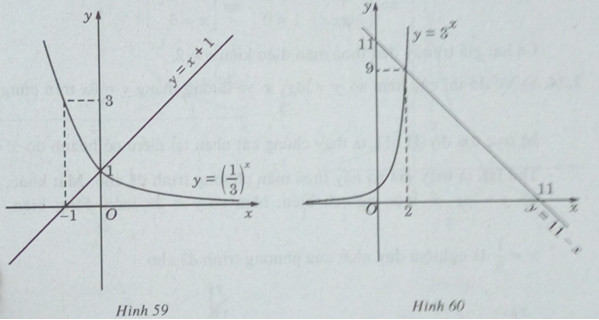
Giải SBT Toán 12 bài 5: Phương trình mũ và phương trình logarit

d) Vẽ đồ thị của hàm số và đường thẳng y = 11 – x trên cùng một hệ trục tọa độ (H.60), ta thấy chúng cắt nhau tại điểm có hoành độ x = 2. Thử lại, ta thấy x = 2 thỏa mãn phương trình đã cho. Mặt khác, y=3^x luôn đồng biến, y = 11 – x luôn nghịch biến. Vậy x = 2 là nghiệm duy nhất.

Bài 2.33 trang 125 Sách bài tập (SBT) Giải tích 12

Giải các phương trình logarit sau:

a) $\log x + \log {x^2} = \log 9x$ $\log x + \log {x^2} = \log 9x$

b) $\log {x^4} + \log 4x = 2 + \log {x^3}$$ $\log {x^4} + \log 4x = 2 + \log {x^3}$$

c) ${\log _4}{\rm{[}}(x + 2)(x + 3){\rm{]}} + {\log _4}\frac{{x - 2}}{{x + 3}} = 2$ ${\log _4}{\rm{[}}(x + 2)(x + 3){\rm{]}} + {\log _4}\frac{{x - 2}}{{x + 3}} = 2$

d) ${\log _{\sqrt 3 }}(x - 2){\log _5}x = 2{\log _3}(x - 2)$ ${\log _{\sqrt 3 }}(x - 2){\log _5}x = 2{\log _3}(x - 2)$

Hướng dẫn làm bài:

a) Với điều kiện x > 0, ta có

$\log x + 2\log x = \log 9 + \log x$ $\log x + 2\log x = \log 9 + \log x$

$\Leftrightarrow \log x = \log 3 \Leftrightarrow x = 3$ $\Leftrightarrow \log x = \log 3 \Leftrightarrow x = 3$

b) Với điều kiện x > 0, ta có

$4\log x + \log 4 + \log x = 2\log 10 + 3\log x$ $4\log x + \log 4 + \log x = 2\log 10 + 3\log x$

$\Leftrightarrow \log x = \log 5 \Leftrightarrow x = 5$ $\Leftrightarrow \log x = \log 5 \Leftrightarrow x = 5$

c) Ta có điều kiện của phương trình đã cho là:

$\left\{ {\matrix{{(x + 2)(x + 3) > 0} \cr {{{x - 2} \over {x + 3}} > 0} \cr} } \right. \Leftrightarrow \left\{ {\matrix{{\left[ {\matrix{{x < - 3} \cr {x > - 2} \cr} } \right.} \cr {\left[ {\matrix{{x < - 3} \cr {x > 2} \cr} } \right.} \cr} } \right. \Leftrightarrow \left[ {\matrix{{x < - 3} \cr {x > 2} \cr} (1)} \right.$ $\left\{ {\matrix{{(x + 2)(x + 3) > 0} \cr {{{x - 2} \over {x + 3}} > 0} \cr} } \right. \Leftrightarrow \left\{ {\matrix{{\left[ {\matrix{{x < - 3} \cr {x > - 2} \cr} } \right.} \cr {\left[ {\matrix{{x < - 3} \cr {x > 2} \cr} } \right.} \cr} } \right. \Leftrightarrow \left[ {\matrix{{x < - 3} \cr {x > 2} \cr} (1)} \right.$

Khi đó, phương trình đã cho tương đương với:

${\log _4}{\rm{[}}(x + 2)(x + 3)\frac{{x - 2}}{{x + 3}}{\rm{]}}$ ${\log _4}{\rm{[}}(x + 2)(x + 3)\frac{{x - 2}}{{x + 3}}{\rm{]}}$

$= {\log _4}16 \Leftrightarrow {x^2} - 4 = 16 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 2\sqrt 5 }\\ {x = - 2\sqrt 5 } \end{array}} \right.$ $= {\log _4}16 \Leftrightarrow {x^2} - 4 = 16 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 2\sqrt 5 }\\ {x = - 2\sqrt 5 } \end{array}} \right.$

Cả hai nghiệm trên đều thỏa mãn điều kiện (1).

d) Với điều kiện x > 2, ta có phương trình

$2{\log _3}(x - 2)({\log _5}x - 1) = 0$ $2{\log _3}(x - 2)({\log _5}x - 1) = 0$

$\Leftrightarrow \left[ {\begin{array}{*{20}{c}} {{{\log }_3}(x - 2) = 0}\\ {{{\log }_5}x - 1 = 0} \end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 3}\\ {x = 5} \end{array}} \right.} \right.$ $\Leftrightarrow \left[ {\begin{array}{*{20}{c}} {{{\log }_3}(x - 2) = 0}\\ {{{\log }_5}x - 1 = 0} \end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 3}\\ {x = 5} \end{array}} \right.} \right.$

Cả hai giá trị này đều thỏa mãn điều kiện x > 2.

Bài 2.34 trang 125 Sách bài tập (SBT) Giải tích 12

Giải các phương trình sau bằng phương pháp đồ thị:

a) ${\log _{\frac{1}{3}}}x = 3x$ ${\log _{\frac{1}{3}}}x = 3x$

b) ${\log _3}x = - x + 11$ ${\log _3}x = - x + 11$

c) ${\log _4}x = \frac{4}{x}$ ${\log _4}x = \frac{4}{x}$

d) ${16^x} = {\log _{\frac{1}{2}}}x$ ${16^x} = {\log _{\frac{1}{2}}}x$

Hướng dẫn làm bài:

a) Vẽ đồ thị của hàm số ${\log _{\frac{1}{3}}}x = 3x$ ${\log _{\frac{1}{3}}}x = 3x$ và đường thẳng y = 3x trên cùng một hệ trục tọa độ (H.61), ta thấy chúng cắt nhau tại điểm có hoành độ $x = \frac{1}{3}$ $x = \frac{1}{3}$

Thử lại, ta thấy giá trị này thỏa mãn phương trình đã cho. Mặt khác, hàm số $y = {\log _{\frac{1}{3}}}x$ $y = {\log _{\frac{1}{3}}}x$ luôn nghịch biến, hàm số y = 3x luôn đồng biến. Vậy $x = \frac{1}{3}$ $x = \frac{1}{3}$ là nghiệm duy nhất của phương trình đã cho.

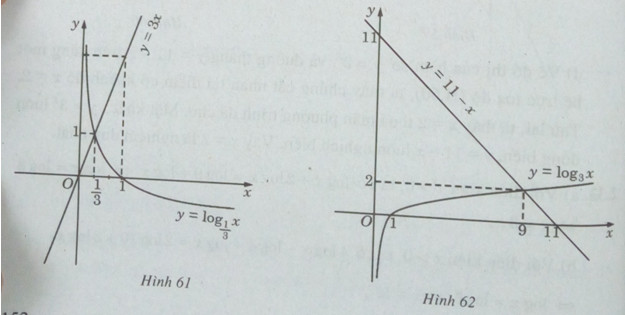
Giải SBT Toán 12 bài 5: Phương trình mũ và phương trình logarit

b) Vẽ đồ thị của hàm số $y = {\log _3}x$ $y = {\log _3}x$ và đường thẳng y = - x + 11 trên cùng một hệ trục tọa độ (H.62) , ta thấy chúng cắt nhau tại điểm có hoành độ x = 9. Lập luận tương tự câu a), ta cũng có đây là nghiệm duy nhất của phương trình đã cho.

c) Vẽ đồ thị của các hàm số $y = {\log _4}x$ $y = {\log _4}x$ và $y = \frac{4}{x}$ $y = \frac{4}{x}$ trên cùng một hệ trục tọa độ (H.63), ta thấy chúng cắt nhau tại điểm có hoành độ x = 4. Ta cũng có hàm số $y = {\log _3}x$ $y = {\log _3}x$ luôn đồng biến, hàm số $y = \frac{4}{x}$ $y = \frac{4}{x}$ luôn nghịch biến trên $(0; + \infty )$ $(0; + \infty )$. Do đó, x = 4 là nghiệm duy nhất.

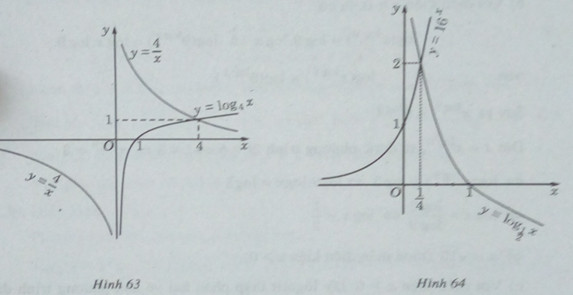
Giải SBT Toán 12 bài 5: Phương trình mũ và phương trình logarit

p>d) Vẽ đồ thị của các hàm số $y = {16^x}$ $y = {16^x}$ và $y = {\log _{\frac{1}{2}}}x$ $y = {\log _{\frac{1}{2}}}x$ trên cùng một hệ trục tọa độ (H.64), ta thấy chúng cắt nhau tại điểm có hoành độ $x = \frac{1}{4}$ $x = \frac{1}{4}$. Thử lại, ta thấy $x = \frac{1}{4}$ $x = \frac{1}{4}$ thỏa mãn phương trình đã cho. Mặt khác, hàm số luôn đồng biến, hàm số luôn nghịch biến.

Vậy $x = \frac{1}{4}$ $x = \frac{1}{4}$ là nghiệm duy nhất của phương trình.

Bài 2.35 trang 125 Sách bài tập (SBT) Giải tích 12

Giải các phương trình logarit:

a) ${\log _2}({2^x} + 1).{\log _2}({2^{x + 1}} + 2) = 2$ ${\log _2}({2^x} + 1).{\log _2}({2^{x + 1}} + 2) = 2$

b) ${x^{\log 9}} + {9^{\log x}} = 6$ ${x^{\log 9}} + {9^{\log x}} = 6$

c) ${x^{3{{\log }^3}x - \frac{2}{3}\log x}} = 100\sqrt[3]{{10}}$ ${x^{3{{\log }^3}x - \frac{2}{3}\log x}} = 100\sqrt[3]{{10}}$

d) $1 + 2{\log _{x + 2}}5 = {\log _5}(x + 2)$ $1 + 2{\log _{x + 2}}5 = {\log _5}(x + 2)$

Hướng dẫn làm bài:

a) ${\log _2}({2^x} + 1).{\log _2}{\rm{[}}2({2^x} + 1){\rm{]}} = 2$ ${\log _2}({2^x} + 1).{\log _2}{\rm{[}}2({2^x} + 1){\rm{]}} = 2$

$\Leftrightarrow {\log _2}({2^x} + 1).{\rm{[}}1 + {\log _2}({2^x} + 1){\rm{]}} = 2$ $\Leftrightarrow {\log _2}({2^x} + 1).{\rm{[}}1 + {\log _2}({2^x} + 1){\rm{]}} = 2$

Đặt $t = {\log _2}({2^x} + 1)$ $t = {\log _2}({2^x} + 1)$, ta có phương trình

$t(1 + t) = 2 ⇔ {t^2} + t – 2 = 0 \eqalign{& \Leftrightarrow \left[ {\matrix{{t = 1} \cr {t = - 2} \cr} } \right. \Leftrightarrow \left[ {\matrix{{{{\log }_2}({2^x} + 1) = 1} \cr {{{\log }_2}({2^x} + 1) = - 2} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{{2^x} + 1 = 2} \cr {{2^x} + 1 = {1 \over 4}} \cr} } \right. \Leftrightarrow \left[ {\matrix{{{2^x} = 1} \cr {{2^x} = - {3 \over 4}(l)} \cr} } \right. \Leftrightarrow x = 0 \cr}$ $t(1 + t) = 2 ⇔ {t^2} + t – 2 = 0 \eqalign{& \Leftrightarrow \left[ {\matrix{{t = 1} \cr {t = - 2} \cr} } \right. \Leftrightarrow \left[ {\matrix{{{{\log }_2}({2^x} + 1) = 1} \cr {{{\log }_2}({2^x} + 1) = - 2} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{{2^x} + 1 = 2} \cr {{2^x} + 1 = {1 \over 4}} \cr} } \right. \Leftrightarrow \left[ {\matrix{{{2^x} = 1} \cr {{2^x} = - {3 \over 4}(l)} \cr} } \right. \Leftrightarrow x = 0 \cr}$

b) Với điều kiện x > 0, ta có: $\log ({x^{\log 9}}) = \log ({9^{\log x}})$ $\log ({x^{\log 9}}) = \log ({9^{\log x}})$

$\log ({x^{\log 9}}) = \log 9.\log x$ $\log ({x^{\log 9}}) = \log 9.\log x$ và $\log ({9^{\log x}}) = \log x.\log 9$ $\log ({9^{\log x}}) = \log x.\log 9$

Nên $\log ({x^{\log 9}}) = \log ({9^{\log x}})$ $\log ({x^{\log 9}}) = \log ({9^{\log x}})$

Suy ra:

${t^4} + 14{t^2} - 32t + 17 = 0 \Leftrightarrow {(t - 1)^2}({t^2} + 2t + 17) = 0 \Leftrightarrow t = 1{x^{\log 9}} = {9^{\log x}}$ ${t^4} + 14{t^2} - 32t + 17 = 0 \Leftrightarrow {(t - 1)^2}({t^2} + 2t + 17) = 0 \Leftrightarrow t = 1{x^{\log 9}} = {9^{\log x}}$

Đặt $t = {x^{\log 9}}$ $t = {x^{\log 9}}$, ta được phương trình $2t = 6 ⇔ t = 3 ⇔ {x^{\log 9}} = 3$ $2t = 6 ⇔ t = 3 ⇔ {x^{\log 9}} = 3$

$\eqalign{ & \Leftrightarrow \log ({x^{\log 9}}) = \log 3 \cr & \Leftrightarrow \log 9.\log x = \log 3 \cr & \Leftrightarrow \log x = {{\log 3} \over {\log 9}} \cr & \Leftrightarrow \log x = {1 \over 2} \cr}$ $\eqalign{ & \Leftrightarrow \log ({x^{\log 9}}) = \log 3 \cr & \Leftrightarrow \log 9.\log x = \log 3 \cr & \Leftrightarrow \log x = {{\log 3} \over {\log 9}} \cr & \Leftrightarrow \log x = {1 \over 2} \cr}$

$\Leftrightarrow x = \sqrt {10}$ $\Leftrightarrow x = \sqrt {10}$ (thỏa mãn điều kiện x > 0)

c) Với điều kiện x > 0, lấy logarit thập phân hai vế của phương trình đã cho, ta được:

$(3{\log ^3}x - \frac{2}{3}\log x).\log x = \frac{7}{3}$ $(3{\log ^3}x - \frac{2}{3}\log x).\log x = \frac{7}{3}$

Đặt $t = \log x$ $t = \log x$, ta được phương trình $3{t^4} - \frac{2}{3}{t^2} - \frac{7}{3} = 0$ $3{t^4} - \frac{2}{3}{t^2} - \frac{7}{3} = 0$

$\eqalign{ & \Leftrightarrow 9{t^4} - 2{t^2} - 7 = 0 \Leftrightarrow \left[ \matrix{ {t^2} = 1 \hfill \cr {t^2} = - {7 \over 9}\left( {loại} \right) \hfill \cr} \right.\left[ \matrix{ t = 1 \hfill \cr t = - 1 \hfill \cr} \right. \cr & \Leftrightarrow \left[ \matrix{ \log x = 1 \hfill \cr \log x = - 1 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{ x = 10 \hfill \cr x = {1 \over {10}} \hfill \cr} \right. \cr}$ $\eqalign{ & \Leftrightarrow 9{t^4} - 2{t^2} - 7 = 0 \Leftrightarrow \left[ \matrix{ {t^2} = 1 \hfill \cr {t^2} = - {7 \over 9}\left( {loại} \right) \hfill \cr} \right.\left[ \matrix{ t = 1 \hfill \cr t = - 1 \hfill \cr} \right. \cr & \Leftrightarrow \left[ \matrix{ \log x = 1 \hfill \cr \log x = - 1 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{ x = 10 \hfill \cr x = {1 \over {10}} \hfill \cr} \right. \cr}$

d) Đặt $t = {\log _5}(x + 2)$ $t = {\log _5}(x + 2)$ với điều kiện $x + 2{\rm{ }} > 0,\,\,x + 2 \ne 1$ $x + 2{\rm{ }} > 0,\,\,x + 2 \ne 1$, ta có:

$\eqalign{& 1 + {2 \over t} = t \Leftrightarrow {t^2} - t - 2 = 0,t \ne 0 \cr & \Leftrightarrow \left[ {\matrix{{t = - 1} \cr {t = 2} \cr} } \right. \Leftrightarrow \left[ {\matrix{{{{\log }_5}(x + 2) = - 1} \cr {{{\log }_5}(x + 2) = 2} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{x + 2 = {1 \over 5}} \cr {x + 2 = 25} \cr} \Leftrightarrow \left[ {\matrix{{x = - {9 \over 5}} \cr {x = 23} \cr} } \right.} \right. \cr}$ $\eqalign{& 1 + {2 \over t} = t \Leftrightarrow {t^2} - t - 2 = 0,t \ne 0 \cr & \Leftrightarrow \left[ {\matrix{{t = - 1} \cr {t = 2} \cr} } \right. \Leftrightarrow \left[ {\matrix{{{{\log }_5}(x + 2) = - 1} \cr {{{\log }_5}(x + 2) = 2} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{x + 2 = {1 \over 5}} \cr {x + 2 = 25} \cr} \Leftrightarrow \left[ {\matrix{{x = - {9 \over 5}} \cr {x = 23} \cr} } \right.} \right. \cr}$

Bài 2.36 trang 126 Sách bài tập (SBT) Giải tích 12

Giải phương trình 25^x−6.5^x+5=0 (Đề thi tốt nghiệp THPT năm 2009)

Hướng dẫn làm bài:

Đáp số: x = 0; x = 1.

Bài 2.37 trang 126 Sách bài tập (SBT) Giải tích 12

Giải phương trình: ${4^{2x + \sqrt {x + 2} }} + {2^{{x^3}}} = {4^{2 + \sqrt {x + 2} }} + {2^{{x^3} + 4x - 4}}$ ${4^{2x + \sqrt {x + 2} }} + {2^{{x^3}}} = {4^{2 + \sqrt {x + 2} }} + {2^{{x^3} + 4x - 4}}$(Đề thi đại học năm 2010, khối D)

Hướng dẫn làm bài:

Điều kiện: $x \ge - 2$ $x \ge - 2$

Phương trình tương đương với:

$({2^{4x}} - {2^4})({2^{2\sqrt {x + 2} }} - {2^{{x^3} - 4}}) = 0$ $({2^{4x}} - {2^4})({2^{2\sqrt {x + 2} }} - {2^{{x^3} - 4}}) = 0$. Suy ra:

$\Leftrightarrow \left[ {\begin{array}{*{20}{c}} {{2^{4x}} - {2^4} = 0}\\ {{2^{2\sqrt {x + 2} }} - {2^{{x^3} - 4}} = 0} \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 1}\\ {2\sqrt {x + 2} = {x^3} - 4} \end{array}} \right.$ $\Leftrightarrow \left[ {\begin{array}{*{20}{c}} {{2^{4x}} - {2^4} = 0}\\ {{2^{2\sqrt {x + 2} }} - {2^{{x^3} - 4}} = 0} \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 1}\\ {2\sqrt {x + 2} = {x^3} - 4} \end{array}} \right.$

Nhận thấy $x \ge \sqrt[3]{4}$ $x \ge \sqrt[3]{4}$ và phương trình có một nghiệm x = 2. Trên ${\rm{[}}\sqrt[3]{4}; + \infty )$ ${\rm{[}}\sqrt[3]{4}; + \infty )$, hàm số $f(x) = 2\sqrt {x + 2} - {x^3} + 4$ $f(x) = 2\sqrt {x + 2} - {x^3} + 4$ có đạo hàm $f(x) = 2\sqrt {x + 2} - {x^3} + 4$ $f(x) = 2\sqrt {x + 2} - {x^3} + 4$ nên f(x) luôn nghịch biến. Suy ra x = 2 là nghiệm duy nhất.

Vậy phương trình có nghiệm x = 1; x = 2.

Bài 2.38 trang 126 Sách bài tập (SBT) Giải tích 12

Giải phương trình:

$f(x) = 2\sqrt {x + 2} - {x^3} + 4{\log _2}(8 - {x^2}) + {\log _{\frac{1}{2}}}(\sqrt {1 + x} + \sqrt {1 - x} ) - 2 = 0$ $f(x) = 2\sqrt {x + 2} - {x^3} + 4{\log _2}(8 - {x^2}) + {\log _{\frac{1}{2}}}(\sqrt {1 + x} + \sqrt {1 - x} ) - 2 = 0$

(Đề thi Đại học năm 2011, khối D)

Hướng dẫn làm bài:

Điều kiện: $- 1 \le x \le 1$ $- 1 \le x \le 1$

Phương trình đã cho tương đương với:

$\eqalign{ & {\log _2}(8 - {x^2}) = {\log _2}{\rm{[}}4(\sqrt {1 + x} + \sqrt {1 - x} ){\rm{]}} \cr & \Leftrightarrow {(8 - {x^2})^2} = 16(2 + 2\sqrt {1 - {x^2}} ) \cr}$ $\eqalign{ & {\log _2}(8 - {x^2}) = {\log _2}{\rm{[}}4(\sqrt {1 + x} + \sqrt {1 - x} ){\rm{]}} \cr & \Leftrightarrow {(8 - {x^2})^2} = 16(2 + 2\sqrt {1 - {x^2}} ) \cr}$

Đặt $t = \sqrt {1 - {x^2}}$ $t = \sqrt {1 - {x^2}}$ ta được:

$\eqalign{ & {t^4} + 14{t^2} - 32t + 17 = 0 \cr & \Leftrightarrow {(t - 1)^2}({t^2} + 2t + 17) = 0 \cr & \Leftrightarrow t = 1 \cr}$ $\eqalign{ & {t^4} + 14{t^2} - 32t + 17 = 0 \cr & \Leftrightarrow {(t - 1)^2}({t^2} + 2t + 17) = 0 \cr & \Leftrightarrow t = 1 \cr}$

Suy ra x = 0. Vậy phương trình có nghiệm x = 0

---------------------------------

Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải SBT Toán 12 bài 5: Phương trình mũ và phương trình logarit. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán lớp 12, Giải bài tập Hóa học lớp 12, Giải bài tập Vật Lí 12 mà VnDoc tổng hợp và đăng tải.