Toán lớp 5 VNEN bài 2: Ôn tập so sánh hai phân số

Giải Toán lớp 5 VNEN

Giải Toán lớp 5 VNEN bài 2: Ôn tập so sánh hai phân số Sách VNEN toán 5 tập 1 bao gồm chi tiết lời giải cho từng bài tập giúp các em học sinh lớp 5 củng cố, rèn kỹ năng giải Toán về phân số. Mời các em học sinh tham khảo lời giải hay sau đây.

Toán 5 VNEN Bài 2 Ôn tập so sánh hai phân số

A. Hoạt động thực hành Ôn tập về so sánh phân số Toán lớp 5
B. Hoạt động ứng dụng Ôn tập so sánh hai phân số Toán lớp 5
C. Giải bài tập SGK, VBT Ôn tập so sánh hai phân số
D. Trắc nghiệm Ôn tập so sánh hai phân số

A. Hoạt động thực hành Ôn tập về so sánh phân số Toán lớp 5

Câu 1 Trang 8 VNEN toán 5 tập 1

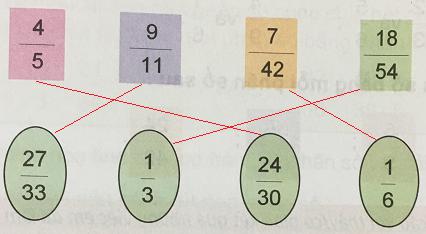
Chơi trò chơi “ ghép thẻ”:

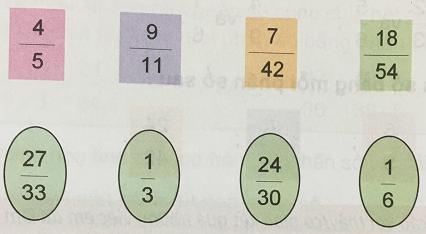
Giải Toán lớp 5 VNEN bài Ôn tập so sánh hai phân số

Đáp án và hướng dẫn giải

Áp dụng tính chất cơ bản của phân số

- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.

- Nếu chia hết cả tử số và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.

Giải Toán lớp 5 VNEN bài Ôn tập so sánh hai phân số

Câu 2 Trang 8 VNEN toán 5 tập 1

Thảo luận để điền dấu (> = < ) thích hợp vào chỗ chấm:

a) $\dfrac{2}{7}...\dfrac{5}{7};\,\, \dfrac{3}{4}...\dfrac{1}{4};\,\, \dfrac{5}{{13}}...\dfrac{5}{{13}}$ $\dfrac{2}{7}...\dfrac{5}{7};\,\, \dfrac{3}{4}...\dfrac{1}{4};\,\, \dfrac{5}{{13}}...\dfrac{5}{{13}}$

b) $\dfrac{5}{6}...\dfrac{2}{3};\,\, \dfrac{3}{4}...\dfrac{5}{{13}};\,\, \dfrac{8}{{20}}...\dfrac{2}{5}$ $\dfrac{5}{6}...\dfrac{2}{3};\,\, \dfrac{3}{4}...\dfrac{5}{{13}};\,\, \dfrac{8}{{20}}...\dfrac{2}{5}$

Đáp án và hướng dẫn giải

Áp dụng các các so sánh hai phân số có cùng mẫu số, so sánh hai phân số khác mẫu số đã học ở lớp 4.

a) $\dfrac{2}{7} < \dfrac{5}{7};\,\, \dfrac{3}{4} > \dfrac{1}{4};\,\, \dfrac{5}{{13}} = \dfrac{5}{{13}}$ $\dfrac{2}{7} < \dfrac{5}{7};\,\, \dfrac{3}{4} > \dfrac{1}{4};\,\, \dfrac{5}{{13}} = \dfrac{5}{{13}}$

b) +) Ta có: $\dfrac{2}{3} = \dfrac{{2 \times 2}}{{3 \times 2}} = \dfrac{4}{6}$ $\dfrac{2}{3} = \dfrac{{2 \times 2}}{{3 \times 2}} = \dfrac{4}{6}$. Vì $\dfrac{5}{6} > \dfrac{4}{6}$ $\dfrac{5}{6} > \dfrac{4}{6}$ nên $\dfrac{5}{6} > \dfrac{2}{3};$ $\dfrac{5}{6} > \dfrac{2}{3};$,

+) Ta có: $\dfrac{3}{4} = \dfrac{{3 \times 13}}{{4 \times 13}} = \dfrac{{39}}{{52}} ; \dfrac{5}{{13}} = \dfrac{{5 \times 4}}{{13 \times 4}} = \dfrac{{20}}{{52}}$ $\dfrac{3}{4} = \dfrac{{3 \times 13}}{{4 \times 13}} = \dfrac{{39}}{{52}} ; \dfrac{5}{{13}} = \dfrac{{5 \times 4}}{{13 \times 4}} = \dfrac{{20}}{{52}}$

Vì $\dfrac{{39}}{{52}} > \dfrac{{20}}{{52}}$ $\dfrac{{39}}{{52}} > \dfrac{{20}}{{52}}$ nên $\dfrac{3}{4} > \dfrac{5}{{13}}$ $\dfrac{3}{4} > \dfrac{5}{{13}}$;

+) $\dfrac{2}{5} = \dfrac{{2 \times 4}}{{4 \times 4}} = \dfrac{8}{{20}}$ $\dfrac{2}{5} = \dfrac{{2 \times 4}}{{4 \times 4}} = \dfrac{8}{{20}}$. Vì $\dfrac{8}{{20}} = \dfrac{8}{{20}}$ $\dfrac{8}{{20}} = \dfrac{8}{{20}}$ nên $\dfrac{8}{{20}} = \dfrac{2}{5}$ $\dfrac{8}{{20}} = \dfrac{2}{5}$.

Câu 3 Trang 8 VNEN toán 5 tập 1

a. Thảo luận nội dung cần điền tiếp vào chỗ chấm và nghe thầy (cô) hướng dẫn:

Trong hai phân số cùng mẫu số:

· Phân số có tử số bé hơn thì ………

· Phân số có tử số lớn hơn thì ……….

· Nếu tử số bằng nhau thì hai phân số đó ……….

· Muốn so sánh hai phân số khác mẫu số, ta …….. mẫu số hai phân số đó rồi so sánh các ….. của chúng.

Ví dụ: .....

b. Thảo luận với bạn để điền từ “ bé hơn”, “lớn hơn” hoặc “bằng” vào chỗ chấm trong các nhận xét sau cho đúng:

Nhận xét 1:

· Phân số có tử số lớn hơn mẫu số thì phân số đó ………. 1

· Phân số có tử số bé hơn mẫu số thì phân số đó ……….. 1

· Phân số có tử số bằng mẫu số thì phân số đó ……….. 1

Nhận xét 2: Trong hai phân số có cùng tử số:

· Phân số có mẫu số bé hơn thì …………

· Phân số có mẫu số lớn hơn thì ………..

Ví dụ: ...

Đáp án và hướng dẫn giải

a. Thảo luận nội dung cần điền tiếp vào chỗ chấm và nghe thầy (cô) hướng dẫn:

Trong hai phân số cùng mẫu số:

Phân số có tử số bé hơn thì bé hơn

Phân số có tử số lớn hơn thì lớn hơn

Nếu tử số bằng nhau thì hai phân số đó bằng nhau

Muốn so sánh hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số đó rồi so sánh các tử số của chúng.

*) Ví dụ minh họa về so sánh hai phân số khác mẫu số

So sánh hai phân số: $\frac{4}{5}$ $\frac{4}{5}$ và $\frac{5}{8}$ $\frac{5}{8}$

Ta có: $\dfrac{4}{5} = \dfrac{{4 \times 8}}{{5 \times 8}} = \dfrac{{32}}{{40}}$ $\dfrac{4}{5} = \dfrac{{4 \times 8}}{{5 \times 8}} = \dfrac{{32}}{{40}}$ ; $\dfrac{5}{8} = \dfrac{{5 \times 5}}{{8 \times 5}} = \dfrac{{25}}{{40}}$ $\dfrac{5}{8} = \dfrac{{5 \times 5}}{{8 \times 5}} = \dfrac{{25}}{{40}}$

Vì: $\frac{32}{40}$ $\frac{32}{40}$ > $\frac{25}{40}$ $\frac{25}{40}$nên: $\frac{4}{5} > \frac{5}{8}$ $\frac{4}{5} > \frac{5}{8}$

b. Thảo luận với bạn để điền từ “ bé hơn”, “lớn hơn” hoặc “bằng” vào chỗ chấm trong các nhận xét sau cho đúng:

Nhận xét 1:

Phân số có tử số lớn hơn mẫu số thì phân số đó lớn hơn 1

Phân số có tử số bé hơn mẫu số thì phân số đó bé hơn 1

Phân số có tử số bằng mẫu số thì phân số đó bằng 1

Nhận xét 2: Trong hai phân số có cùng tử số:

Phân số có mẫu số bé hơn thì lớn hơn

Phân số có mẫu số lớn hơn thì bé hơn

*) Ví dụ minh họa về so sánh hai phân số có cùng tử số :

Điền dấu (>, =, < ) thích hợp vào chỗ chấm :

$\dfrac{{35}}{{101}} > \dfrac{{35}}{{123}}$ $\dfrac{{35}}{{101}} > \dfrac{{35}}{{123}}$ ;

Câu 4 Trang 9 VNEN toán 5 tập 1

Điền dấu thích hợp (< , =, >) vào chỗ chấm:

a) $\dfrac{3}{{10}}...\dfrac{7}{{10}};\,\, \dfrac{5}{8}...\dfrac{3}{8};\,\, \dfrac{{25}}{{31}}...\dfrac{{19}}{{31}}$ $\dfrac{3}{{10}}...\dfrac{7}{{10}};\,\, \dfrac{5}{8}...\dfrac{3}{8};\,\, \dfrac{{25}}{{31}}...\dfrac{{19}}{{31}}$

b) $\dfrac{7}{8}...\dfrac{5}{6}; \,\,\dfrac{2}{5}...\dfrac{3}{7}; \,\,\dfrac{1}{4}...\dfrac{1}{6}$ $\dfrac{7}{8}...\dfrac{5}{6}; \,\,\dfrac{2}{5}...\dfrac{3}{7}; \,\,\dfrac{1}{4}...\dfrac{1}{6}$

c) $\dfrac{2}{5}...1;\,\, \dfrac{7}{6}...1;\, \,\dfrac{{21}}{{21}}...1$ $\dfrac{2}{5}...1;\,\, \dfrac{7}{6}...1;\, \,\dfrac{{21}}{{21}}...1$

d) $\dfrac{7}{6}...\dfrac{7}{4};\,\, \, \dfrac{{12}}{{17}}...\dfrac{{12}}{{13}};\, \,\,\dfrac{2}{3}...\dfrac{2}{5}$ $\dfrac{7}{6}...\dfrac{7}{4};\,\, \, \dfrac{{12}}{{17}}...\dfrac{{12}}{{13}};\, \,\,\dfrac{2}{3}...\dfrac{2}{5}$

Đáp án và hướng dẫn giải

a) $\dfrac{3}{{10}} < \dfrac{7}{{10}};\,\, \dfrac{5}{8} > \dfrac{3}{8};\,\, \dfrac{{25}}{{31}} > \dfrac{{19}}{{31}}$ $\dfrac{3}{{10}} < \dfrac{7}{{10}};\,\, \dfrac{5}{8} > \dfrac{3}{8};\,\, \dfrac{{25}}{{31}} > \dfrac{{19}}{{31}}$

b) Ta có :

+) $\dfrac{7}{8} = \dfrac{{7 \times 3}}{{8 \times 3}} = \dfrac{{21}}{{24}} ; \dfrac{5}{6} = \dfrac{{5 \times 4}}{{6 \times 4}} = \dfrac{{20}}{{24}}$ $\dfrac{7}{8} = \dfrac{{7 \times 3}}{{8 \times 3}} = \dfrac{{21}}{{24}} ; \dfrac{5}{6} = \dfrac{{5 \times 4}}{{6 \times 4}} = \dfrac{{20}}{{24}}$

Vì $\dfrac{{21}}{{24}} > \dfrac{{20}}{{24}}$ $\dfrac{{21}}{{24}} > \dfrac{{20}}{{24}}$ nên $\dfrac{7}{8} > \dfrac{5}{6}$ $\dfrac{7}{8} > \dfrac{5}{6}$;

+) $\dfrac{2}{5} = \dfrac{{2 \times 7}}{{5 \times 7}} = \dfrac{{14}}{{35}} ; \dfrac{3}{7} = \dfrac{{3 \times 5}}{{7 \times 5}} = \dfrac{{15}}{{35}}$ $\dfrac{2}{5} = \dfrac{{2 \times 7}}{{5 \times 7}} = \dfrac{{14}}{{35}} ; \dfrac{3}{7} = \dfrac{{3 \times 5}}{{7 \times 5}} = \dfrac{{15}}{{35}}$

Vì $\dfrac{{14}}{{35}} < \dfrac{{15}}{{35}}$ $\dfrac{{14}}{{35}} < \dfrac{{15}}{{35}}$ nên $\,\dfrac{2}{5} < \dfrac{3}{7}$ $\,\dfrac{2}{5} < \dfrac{3}{7}$;

+) $\dfrac{1}{4} > \dfrac{1}{6}$ $\dfrac{1}{4} > \dfrac{1}{6}$ (vì 4 < 6)

Vậy: $\dfrac{7}{8} > \dfrac{5}{6}; \,\,\dfrac{2}{5} < \dfrac{3}{7}; \,\,\dfrac{1}{4} > \dfrac{1}{6}$ $\dfrac{7}{8} > \dfrac{5}{6}; \,\,\dfrac{2}{5} < \dfrac{3}{7}; \,\,\dfrac{1}{4} > \dfrac{1}{6}$

c) $\dfrac{2}{5} < 1;\,\, \dfrac{7}{6} > 1;\, \,\dfrac{{21}}{{21}} = 1$ $\dfrac{2}{5} < 1;\,\, \dfrac{7}{6} > 1;\, \,\dfrac{{21}}{{21}} = 1$

d) $\dfrac{7}{6} < \dfrac{7}{4};\,\, \, \dfrac{{12}}{{17}} < \dfrac{{12}}{{13}};\, \,\,\dfrac{2}{3} > \dfrac{2}{5}$ $\dfrac{7}{6} < \dfrac{7}{4};\,\, \, \dfrac{{12}}{{17}} < \dfrac{{12}}{{13}};\, \,\,\dfrac{2}{3} > \dfrac{2}{5}$

Câu 5 Trang 9 VNEN toán 5 tập 1

a. Viết các phân số theo thứ tự từ bé đến lớn $\dfrac{2}{3};\,\dfrac{3}{7};\,\dfrac{5}{9}$ $\dfrac{2}{3};\,\dfrac{3}{7};\,\dfrac{5}{9}$

b. Viết các phân số theo thứ tự từ lớn đến bé $\dfrac{5}{{18}};\dfrac{4}{3};\dfrac{5}{6}$ $\dfrac{5}{{18}};\dfrac{4}{3};\dfrac{5}{6}$

Đáp án và hướng dẫn giải

a) Chọn MSC là 63. Quy đồng mẫu số các phân số ta có :

$\dfrac{2}{3} = \dfrac{{2 \times 21}}{{3 \times 21}} = \dfrac{{42}}{{63}}; \dfrac{3}{7} = \dfrac{{3 \times 9}}{{7 \times 9}} = \dfrac{{27}}{{63}}; \dfrac{5}{9} = \dfrac{{5 \times 7}}{{9 \times 7}} = \dfrac{{35}}{{63}}$ $\dfrac{2}{3} = \dfrac{{2 \times 21}}{{3 \times 21}} = \dfrac{{42}}{{63}}; \dfrac{3}{7} = \dfrac{{3 \times 9}}{{7 \times 9}} = \dfrac{{27}}{{63}}; \dfrac{5}{9} = \dfrac{{5 \times 7}}{{9 \times 7}} = \dfrac{{35}}{{63}}$

Vì $\dfrac{{27}}{{63}} < \dfrac{{35}}{{63}} < \dfrac{{42}}{{63}}$ $\dfrac{{27}}{{63}} < \dfrac{{35}}{{63}} < \dfrac{{42}}{{63}}$nên $\dfrac{3}{7}\,\, < \,\,\dfrac{5}{9}\,\, < \,\,\dfrac{2}{3}$ $\dfrac{3}{7}\,\, < \,\,\dfrac{5}{9}\,\, < \,\,\dfrac{2}{3}$.

Vậy các phân số đã cho viết theo thứ tự từ bé đến lớn là $\dfrac{3}{7}\,\,;\,\,\,\dfrac{5}{9}\,\,;\,\,\,\dfrac{2}{3}$ $\dfrac{3}{7}\,\,;\,\,\,\dfrac{5}{9}\,\,;\,\,\,\dfrac{2}{3}$:

b) Chọn MSC là 18. Quy đồng mẫu số các phân số ta có :

$\dfrac{4}{3} = \dfrac{{4 \times 6}}{{3 \times 6}} = \dfrac{{24}}{{18}}; \dfrac{5}{6} = \dfrac{{5 \times 3}}{{6 \times 3}} = \dfrac{{15}}{{18}};$ $\dfrac{4}{3} = \dfrac{{4 \times 6}}{{3 \times 6}} = \dfrac{{24}}{{18}}; \dfrac{5}{6} = \dfrac{{5 \times 3}}{{6 \times 3}} = \dfrac{{15}}{{18}};$

Giữ nguyên phân số $\dfrac{5}{{18}}$ $\dfrac{5}{{18}}$.

Vì $\dfrac{{24}}{{18}} > \dfrac{{15}}{{18}} > \dfrac{5}{{18}}$ $\dfrac{{24}}{{18}} > \dfrac{{15}}{{18}} > \dfrac{5}{{18}}$ nên $\dfrac{4}{3}\,\, > \,\,\dfrac{5}{6}\,\, > \,\,\dfrac{5}{{18}}$ $\dfrac{4}{3}\,\, > \,\,\dfrac{5}{6}\,\, > \,\,\dfrac{5}{{18}}$.

Vậy các phân số đã cho viết theo thứ tự từ lớn đến bé là: $\dfrac{4}{3}\,\,;\,\,\,\dfrac{5}{6}\,\,;\,\,\,\dfrac{5}{{18}}$ $\dfrac{4}{3}\,\,;\,\,\,\dfrac{5}{6}\,\,;\,\,\,\dfrac{5}{{18}}$.

B. Hoạt động ứng dụng Ôn tập so sánh hai phân số Toán lớp 5

Mẹ Linh dùng $\frac{2}{5}$ $\frac{2}{5}$diện tích của mảnh vườn để trồng hoa và dùng $\frac{1}{4}$ $\frac{1}{4}$ diện tích của mảnh vườn để trồng rau thơm. Em hãy so sánh diện tích trồng rau thơm với diện tích trồng hoa xem diện tích nào lớn hơn.

Đáp án và hướng dẫn giải

Phương pháp:

Ta quy về so sánh hai phân số $\dfrac{2}{5}$ $\dfrac{2}{5}$ và $\dfrac{1}{4}$ $\dfrac{1}{4}$bằng cách quy đồng mẫu số hai phân số, sau đó so sánh tử số của chúng.

Lời giải:

Ta sẽ so sánh hai phân số $\dfrac{2}{5}$ $\dfrac{2}{5}$ và $\dfrac{1}{4}$ $\dfrac{1}{4}$.

Chọn MSC là 20. Ta có :

$\dfrac{2}{5} = \dfrac{{2 \times 4}}{{5 \times 4}} = \dfrac{8}{{20}}; \dfrac{1}{4} = \dfrac{{1 \times 5}}{{4 \times 5}} = \dfrac{5}{{20}}$ $\dfrac{2}{5} = \dfrac{{2 \times 4}}{{5 \times 4}} = \dfrac{8}{{20}}; \dfrac{1}{4} = \dfrac{{1 \times 5}}{{4 \times 5}} = \dfrac{5}{{20}}$

Vì $\dfrac{8}{{20}} > \dfrac{5}{{20}}$ $\dfrac{8}{{20}} > \dfrac{5}{{20}}$ nên $\dfrac{2}{5} > \dfrac{1}{4}$ $\dfrac{2}{5} > \dfrac{1}{4}$.

Vậy diện tích trồng hoa lớn hơn diện tích trồng rau thơm.

C. Giải bài tập SGK, VBT Ôn tập so sánh hai phân số

D. Trắc nghiệm Ôn tập so sánh hai phân số

Trên đây là toàn bộ lời giải sách VNEN môn Toán lớp 5 bài 2 Ôn tập so sánh hai phân số giúp các em học sinh củng cố kiến thức phần giải môn Toán chương trình Công nghệ giáo dục.

>> Bài tiếp theo: Toán lớp 5 VNEN bài 3 Phân số thập phân

Chia sẻ, đánh giá bài viết

52

26.920

Bài trước

Bài sau