Toán lớp 5 VNEN bài 5 Hỗn số

Nằm trong bộ tài liệu Giải SGK Toán lớp 5 VNEN theo từng bài học năm 2023 - 2024, Giải Toán lớp 5 VNEN bài Hỗn số Sách VNEN toán 5 tập 1 bao gồm chi tiết lời giải cho từng bài tập giúp các em học sinh củng cố, rèn kỹ năng giải Toán về phân số. Mời các em học sinh tham khảo lời giải hay sau đây.

A. Hoạt động cơ bản Hỗn số Toán lớp 5

1. Viết theo mẫu:

Trả lời

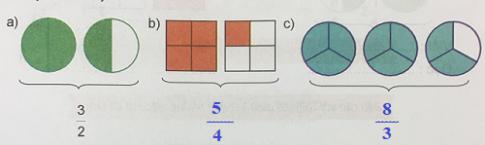
2. Thực hiện lần lượt các hoạt động sau, đọc kĩ nội dung sau và giải thích cho bạn nghe (sgk).

a) Thực hiện lần lượt các hoạt động sau:

• Đọc thông tin và quan sát hình vẽ : Có 2 cái bánh và \(\frac{3}{4}\) cái bánh.

• Em nói : Có 2 và \(\frac{3}{4}\) cái bánh.

• Em viết :  \(2\frac{3}{4}\) cái bánh

b) Đọc kĩ nội dung sau và giải thích cho bạn nghe :

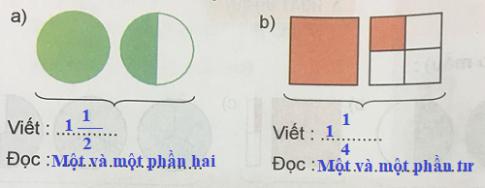
3. Viết rồi đọc hỗn số chỉ phần đã tô màu của mỗi hình vẽ sau:

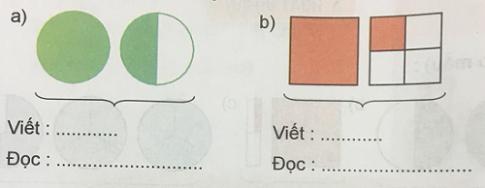
Trả lời:

B. Hoạt động thực hành Hỗn số Toán lớp 5

Câu 1: Trang 16 VNEN toán 5 tập 1

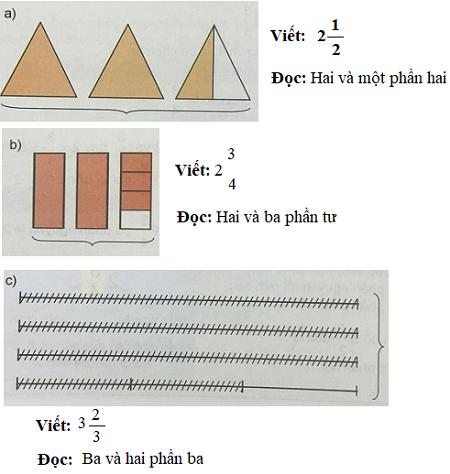
Dựa vào hình vẽ để viết rồi đọc hỗn số thích hợp (theo mẫu):

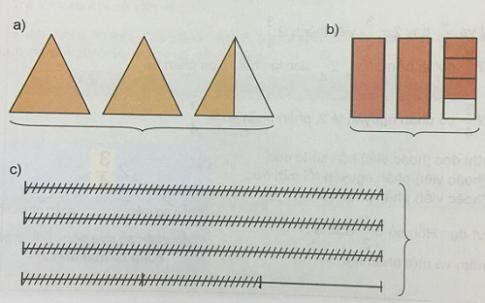
Đáp án

Câu 2: Trang 14 VNEN toán 5 tập 1

Viết hỗn số thích hợp vào chỗ chấm dưới mỗi vạch của tia số:

Đáp án

C. Hoạt động ứng dụng Hỗn số Toán lớp 5

Em đọc mỗi hỗn số sau cho người lớn nghe và chỉ ra phần nguyên, phần phân số của mỗi hỗn số đó: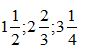

Hỗn số	Đọc	Phần nguyên	Phần phân số
\(1\frac{1}{2}\)	Một và một phần hai	1	12
\(2\frac{2}{3}\)	Hai và hai phần ba	2	23
\(3\frac{1}{4}\)	Ba và một phần tư	3	14

D. Lý thuyết Hỗn số

1. Khái niệm hỗn số

+ Khái niệm: Hỗn số gồm hai thành phần là phần nguyên và phần phân số.

→ Ví dụ: Cho hỗn số \(3\frac{7}{{12}}\)

Phần nguyên của hỗn số là 3 và phần phân số là \(\frac{7}{{12}}\).

Nhận xét: Phần phân số của hỗn số bao giờ cũng bé hơn đơn vị.

+ Cách đọc hỗn số:

- Bước 1: đọc phần nguyên

- Bước 2: đọc “và”

- Bước 3: đọc phần phân số

→ Ví dụ: Hỗn số \(3\frac{7}{{12}}\) được đọc là “ba và bảy phần mười hai”.

2. Cách chuyển hỗn số thành phân số

+ Để chuyển một hỗn số thành phân số, ta thực hiện các bước sau:

- Bước 1: Lấy phần nguyên nhân với mẫu số, kết quả nhận được đem cộng với tử số

- Bước 2: Thay kết quả ở bước 1 thành tử số mới, giữ nguyên mẫu số. Ta được một phân số mới được chuyển từ hỗn số đã cho

→ Ví dụ: Chuyển các hỗn số thành phân số: \(2\frac{1}{6};5\frac{3}{4};2\frac{2}{9}\)

Lời giải:

\(2\frac{1}{6} = \frac{{2 \times 6 + 1}}{6} = \frac{{13}}{6};5\frac{3}{4} = \frac{{5 \times 4 + 3}}{4} = \frac{{23}}{4};2\frac{2}{9} = \frac{{2 \times 9 + 2}}{9} = \frac{{20}}{9}\)

3. Cách chuyển phân số thành hỗn số

+ Để chuyển một phân số sang hỗn số, ta thực hiện theo các bước sau:

- Bước 1: Lấy tử số chia cho mẫu số

- Bước 2: Phần nguyên là số nguyên trong hỗn số

- Bước 3: Phần dư là tử số mới trong hỗn số

- Bước 4: Phần mẫu số giữ nguyên giá trị

→ Ví dụ: Chuyển các phân số thành hỗn số: \(\frac{9}{2};\frac{{16}}{3};\frac{{27}}{5}\)

Lời giải:

Ta có:

9 : 2 = 4 (dư 1); 16 : 3 = 5 (dư 1) và 27 : 5 = 5 (dư 2)

Vậy các phân số đã cho được viết dưới dạng hỗn số là:

\(\frac{9}{2} = 4\frac{1}{2};\frac{{16}}{3} = 5\frac{1}{3};\frac{{27}}{5} = 5\frac{2}{5}\)

* Chú ý: Bất kỳ phân số nào có tử số lớn hơn mẫu số đều có thể đổi thành hỗn số và ngược lại. Tuy nhiên nếu tử số bằng hoặc nhỏ hơn mẫu số thì không thể thực hiện được việc chuyển phân số thành hỗn số.

4. Phép tính hỗn số

+ Tương tự như với phân số, hỗn số có thể thực hiện các phép toán cộng, trừ, nhân, chia với nhau.

+ Để cộng hay trừ hỗn số, ta có hai cách làm sau:

- Cách 1: Chuyển hỗn số về dạng phân số rồi thực hiện các phép toán trên phân số

- Cách 2: Ta tách phần nguyên để thực hiện phép tính cộng trừ, tách phần phân số rồi thực hiện phép tính cộng trừ.

→ Ví dụ: Thực hiện phép tính sau bằng hai cách:

a, \(1\frac{5}{6} + 2\frac{1}{3}\)

b, \(6\frac{1}{4} - 1\frac{1}{{12}}\)

Lời giải:

Cách 1:

a, \(1\frac{5}{6} + 2\frac{1}{3} = \frac{{11}}{6} + \frac{7}{3} = \frac{{11}}{6} + \frac{{14}}{6} = \frac{{25}}{6} = 4\frac{1}{6}\)

b, \(6\frac{1}{4} - 1\frac{1}{{12}} = \frac{{25}}{4} - \frac{{13}}{{12}} = \frac{{75}}{{12}} - \frac{{13}}{{12}} = \frac{{62}}{{12}} = \frac{{31}}{6} = 5\frac{1}{6}\)

Cách 2:

a, \(1\frac{5}{6} + 2\frac{1}{3} = \left( {1 + 2} \right) + \left( {\frac{5}{6} + \frac{1}{3}} \right) = 3 + \left( {\frac{5}{6} + \frac{2}{6}} \right) = 3 + \frac{7}{6} = 3 + 1\frac{1}{6} = 4\frac{1}{6}\)

b, \(6\frac{1}{4} - 1\frac{1}{{12}} = \left( {6 - 1} \right) + \left( {\frac{1}{4} - \frac{1}{{12}}} \right) = 5 + \frac{1}{6} = 5\frac{1}{6}\)

+ Để nhân hoặc chia hỗn số, ta chuyển hỗn số về dạng phân số rồi thực hiện các phép tính nhân chia trên phân số.

Tham khảo:

• Giải vở bài tập Toán 5 bài 9: Hỗn số
• Giải vở bài tập Toán 5 bài 10: Hỗn số (tiếp theo)
• Giải vở bài tập Toán 5 bài 11: Luyện tập hỗn số

Trên đây là Giải SGK Toán lớp 5 VNEN bài 5: Hỗn số. VnDoc.com hy vọng rằng tài liệu Giải SGK môn Toán 5 theo chương trình VNEN trên đây sẽ giúp các em học sinh lớp 5 ôn tập kiến thức hiệu quả.

Ngoài giải bài tập Toán 5 VNEN, VnDoc còn giúp các bạn giải toán lớp 5 sách giáo khoa.